Data-Driven, ML-assisted Approaches to Problem Well-Posedness

Classically, to solve differential equation problems, it is necessary to specify sufficient initial and/or boundary conditions so as to allow the existence of a unique solution. Well-posedness of differential equation problems thus involves studying the existence and uniqueness of solutions, and their dependence to such pre-specified conditions. However, in part due to mathematical necessity, these conditions are usually specified "to arbitrary precision" only on (appropriate portions of) the boundary of the space-time domain. This does not mirror how data acquisition is performed in realistic situations, where one may observe entire "patches" of solution data at arbitrary space-time locations; alternatively one might have access to more than one solutions stemming from the same differential operator. In our short work, we demonstrate how standard tools from machine and manifold learning can be used to infer, in a data driven manner, certain well-posedness features of differential equation problems, for initial/boundary condition combinations under which rigorous existence/uniqueness theorems are not known. Our study naturally combines a data assimilation perspective with an operator-learning one.

Randomized Kaczmarz Methods with Beyond-Krylov Convergence

Randomized Kaczmarz methods form a family of linear system solvers which converge by repeatedly projecting their iterates onto randomly sampled equations. While effective in some contexts, such as highly over-determined least squares, Kaczmarz methods are traditionally deemed secondary to Krylov subspace methods, since this latter family of solvers can exploit outliers in the input's singular value distribution to attain fast convergence on ill-conditioned systems. In this paper, we introduce Kaczmarz++, an accelerated randomized block Kaczmarz algorithm that exploits outlying singular values in the input to attain a fast Krylov-style convergence. Moreover, we show that Kaczmarz++ captures large outlying singular values provably faster than popular Krylov methods, for both over- and under-determined systems. We also develop an optimized variant for positive semidefinite systems, called CD++, demonstrating empirically that it is competitive in arithmetic operations with both CG and GMRES on a collection of benchmark problems. To attain these results, we introduce several novel algorithmic improvements to the Kaczmarz framework, including adaptive momentum acceleration, Tikhonov-regularized projections, and a memoization scheme for reusing information from previously sampled equation~blocks.

Learning nonnegative matrix factorizations from compressed data

We propose a flexible and theoretically supported framework for scalable nonnegative matrix factorization. The goal is to find nonnegative low-rank components directly from compressed measurements, accessing the original data only once or twice. We consider compression through randomized sketching methods that can be adapted to the data, or can be oblivious. We formulate optimization problems that only depend on the compressed data, but which can recover a nonnegative factorization which closely approximates the original matrix. The defined problems can be approached with a variety of algorithms, and in particular, we discuss variations of the popular multiplicative updates method for these compressed problems. We demonstrate the success of our approaches empirically and validate their performance in real-world applications.

On Regularization via Early Stopping for Least Squares Regression

A fundamental problem in machine learning is understanding the effect of early stopping on the parameters obtained and the generalization capabilities of the model. Even for linear models, the effect is not fully understood for arbitrary learning rates and data. In this paper, we analyze the dynamics of discrete full batch gradient descent for linear regression. With minimal assumptions, we characterize the trajectory of the parameters and the expected excess risk. Using this characterization, we show that when training with a learning rate schedule $\eta_k$, and a finite time horizon $T$, the early stopped solution $\beta_T$ is equivalent to the minimum norm solution for a generalized ridge regularized problem. We also prove that early stopping is beneficial for generic data with arbitrary spectrum and for a wide variety of learning rate schedules. We provide an estimate for the optimal stopping time and empirically demonstrate the accuracy of our estimate.

Discrete error dynamics of mini-batch gradient descent for least squares regression

We study the discrete dynamics of mini-batch gradient descent for least squares regression when sampling without replacement. We show that the dynamics and generalization error of mini-batch gradient descent depends on a sample cross-covariance matrix $Z$ between the original features $X$ and a set of new features $\widetilde{X}$, in which each feature is modified by the mini-batches that appear before it during the learning process in an averaged way. Using this representation, we rigorously establish that the dynamics of mini-batch and full-batch gradient descent agree up to leading order with respect to the step size using the linear scaling rule. We also study discretization effects that a continuous-time gradient flow analysis cannot detect, and show that mini-batch gradient descent converges to a step-size dependent solution, in contrast with full-batch gradient descent. Finally, we investigate the effects of batching, assuming a random matrix model, by using tools from free probability theory to numerically compute the spectrum of $Z$.

Fine-grained Analysis and Faster Algorithms for Iteratively Solving Linear Systems

While effective in practice, iterative methods for solving large systems of linear equations can be significantly affected by problem-dependent condition number quantities. This makes characterizing their time complexity challenging, particularly when we wish to make comparisons between deterministic and stochastic methods, that may or may not rely on preconditioning and/or fast matrix multiplication. In this work, we consider a fine-grained notion of complexity for iterative linear solvers which we call the spectral tail condition number, $\kappa_\ell$, defined as the ratio between the $\ell$th largest and the smallest singular value of the matrix representing the system. Concretely, we prove the following main algorithmic result: Given an $n\times n$ matrix $A$ and a vector $b$, we can find $\tilde{x}$ such that $\|A\tilde{x}-b\|\leq\epsilon\|b\|$ in time $\tilde{O}(\kappa_\ell\cdot n^2\log 1/\epsilon)$ for any $\ell = O(n^{\frac1{\omega-1}})=O(n^{0.729})$, where $\omega \approx 2.372$ is the current fast matrix multiplication exponent. This guarantee is achieved by Sketch-and-Project with Nesterov's acceleration. Some of the implications of our result, and of the use of $\kappa_\ell$, include direct improvement over a fine-grained analysis of the Conjugate Gradient method, suggesting a stronger separation between deterministic and stochastic iterative solvers; and relating the complexity of iterative solvers to the ongoing algorithmic advances in fast matrix multiplication, since the bound on $\ell$ improves with $\omega$. Our main technical contributions are new sharp characterizations for the first and second moments of the random projection matrix that commonly arises in sketching algorithms, building on a combination of techniques from combinatorial sampling via determinantal point processes and Gaussian universality results from random matrix theory.

Stochastic gradient descent for streaming linear and rectified linear systems with Massart noise

We propose SGD-exp, a stochastic gradient descent approach for linear and ReLU regressions under Massart noise (adversarial semi-random corruption model) for the fully streaming setting. We show novel nearly linear convergence guarantees of SGD-exp to the true parameter with up to $50\%$ Massart corruption rate, and with any corruption rate in the case of symmetric oblivious corruptions. This is the first convergence guarantee result for robust ReLU regression in the streaming setting, and it shows the improved convergence rate over previous robust methods for $L_1$ linear regression due to a choice of an exponentially decaying step size, known for its efficiency in practice. Our analysis is based on the drift analysis of a discrete stochastic process, which could also be interesting on its own.

Sharp Analysis of Sketch-and-Project Methods via a Connection to Randomized Singular Value Decomposition

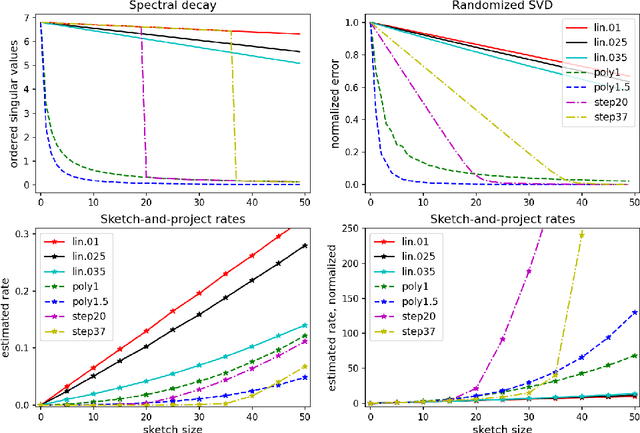
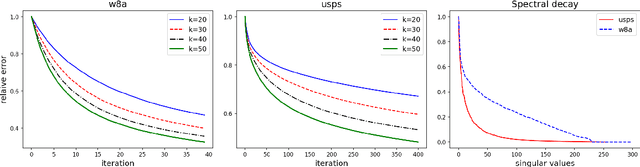
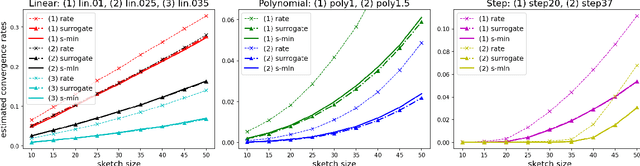
Sketch-and-project is a framework which unifies many known iterative methods for solving linear systems and their variants, as well as further extensions to non-linear optimization problems. It includes popular methods such as randomized Kaczmarz, coordinate descent, variants of the Newton method in convex optimization, and others. In this paper, we obtain sharp guarantees for the convergence rate of sketch-and-project methods via new tight spectral bounds for the expected sketched projection matrix. Our estimates reveal a connection between the sketch-and-project convergence rate and the approximation error of another well-known but seemingly unrelated family of algorithms, which use sketching to accelerate popular matrix factorizations such as QR and SVD. This connection brings us closer to precisely quantifying how the performance of sketch-and-project solvers depends on their sketch size. Our analysis covers not only Gaussian and sub-gaussian sketching matrices, but also a family of efficient sparse sketching methods known as LESS embeddings. Our experiments back up the theory and demonstrate that even extremely sparse sketches show the same convergence properties in practice.

Nonlinear Matrix Approximation with Radial Basis Function Components

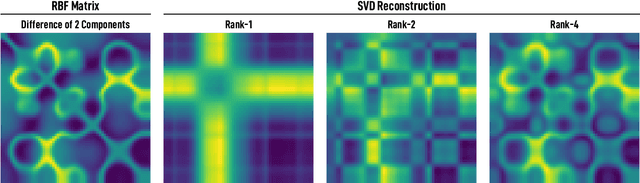
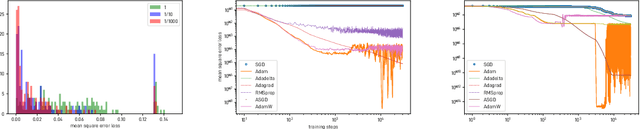
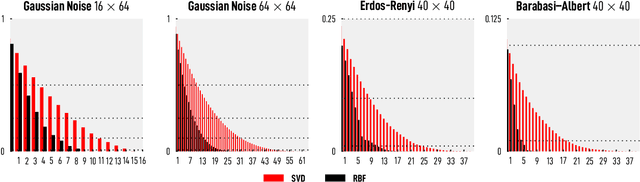
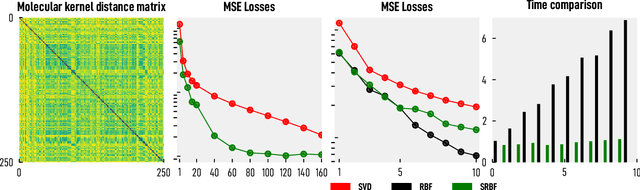
We introduce and investigate matrix approximation by decomposition into a sum of radial basis function (RBF) components. An RBF component is a generalization of the outer product between a pair of vectors, where an RBF function replaces the scalar multiplication between individual vector elements. Even though the RBF functions are positive definite, the summation across components is not restricted to convex combinations and allows us to compute the decomposition for any real matrix that is not necessarily symmetric or positive definite. We formulate the problem of seeking such a decomposition as an optimization problem with a nonlinear and non-convex loss function. Several modern versions of the gradient descent method, including their scalable stochastic counterparts, are used to solve this problem. We provide extensive empirical evidence of the effectiveness of the RBF decomposition and that of the gradient-based fitting algorithm. While being conceptually motivated by singular value decomposition (SVD), our proposed nonlinear counterpart outperforms SVD by drastically reducing the memory required to approximate a data matrix with the same L2 error for a wide range of matrix types. For example, it leads to 2 to 6 times memory save for Gaussian noise, graph adjacency matrices, and kernel matrices. Moreover, this proximity-based decomposition can offer additional interpretability in applications that involve, e.g., capturing the inner low-dimensional structure of the data, retaining graph connectivity structure, and preserving the acutance of images.

Analysis of Legal Documents via Non-negative Matrix Factorization Methods

The California Innocence Project (CIP), a clinical law school program aiming to free wrongfully convicted prisoners, evaluates thousands of mails containing new requests for assistance and corresponding case files. Processing and interpreting this large amount of information presents a significant challenge for CIP officials, which can be successfully aided by topic modeling techniques.In this paper, we apply Non-negative Matrix Factorization (NMF) method and implement various offshoots of it to the important and previously unstudied data set compiled by CIP. We identify underlying topics of existing case files and classify request files by crime type and case status (decision type). The results uncover the semantic structure of current case files and can provide CIP officials with a general understanding of newly received case files before further examinations. We also provide an exposition of popular variants of NMF with their experimental results and discuss the benefits and drawbacks of each variant through the real-world application.