Effective Dynamics of Generative Adversarial Networks

Generative adversarial networks (GANs) are a class of machine-learning models that use adversarial training to generate new samples with the same (potentially very complex) statistics as the training samples. One major form of training failure, known as mode collapse, involves the generator failing to reproduce the full diversity of modes in the target probability distribution. Here, we present an effective model of GAN training, which captures the learning dynamics by replacing the generator neural network with a collection of particles in the output space; particles are coupled by a universal kernel valid for certain wide neural networks and high-dimensional inputs. The generality of our simplified model allows us to study the conditions under which mode collapse occurs. Indeed, experiments which vary the effective kernel of the generator reveal a mode collapse transition, the shape of which can be related to the type of discriminator through the frequency principle. Further, we find that gradient regularizers of intermediate strengths can optimally yield convergence through critical damping of the generator dynamics. Our effective GAN model thus provides an interpretable physical framework for understanding and improving adversarial training.

Cloud-Based Real-Time Molecular Screening Platform with MolFormer

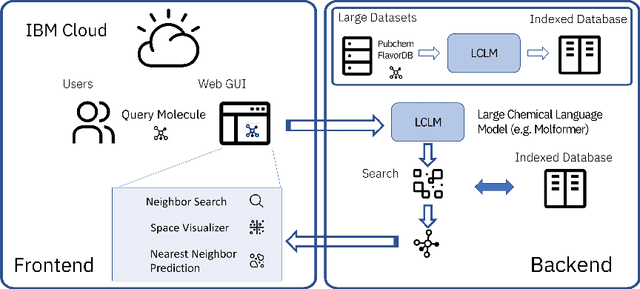
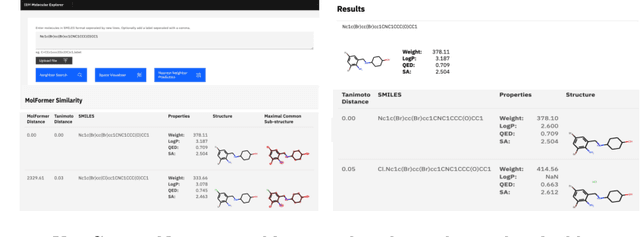
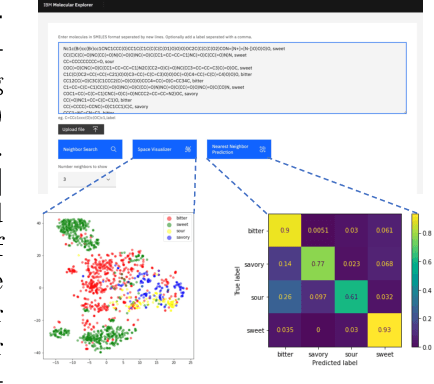
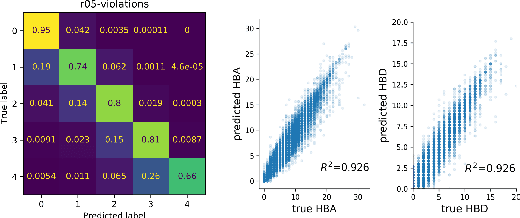
With the prospect of automating a number of chemical tasks with high fidelity, chemical language processing models are emerging at a rapid speed. Here, we present a cloud-based real-time platform that allows users to virtually screen molecules of interest. For this purpose, molecular embeddings inferred from a recently proposed large chemical language model, named MolFormer, are leveraged. The platform currently supports three tasks: nearest neighbor retrieval, chemical space visualization, and property prediction. Based on the functionalities of this platform and results obtained, we believe that such a platform can play a pivotal role in automating chemistry and chemical engineering research, as well as assist in drug discovery and material design tasks. A demo of our platform is provided at \url{www.ibm.biz/molecular_demo}.

Auditing Differential Privacy in High Dimensions with the Kernel Quantum Rényi Divergence

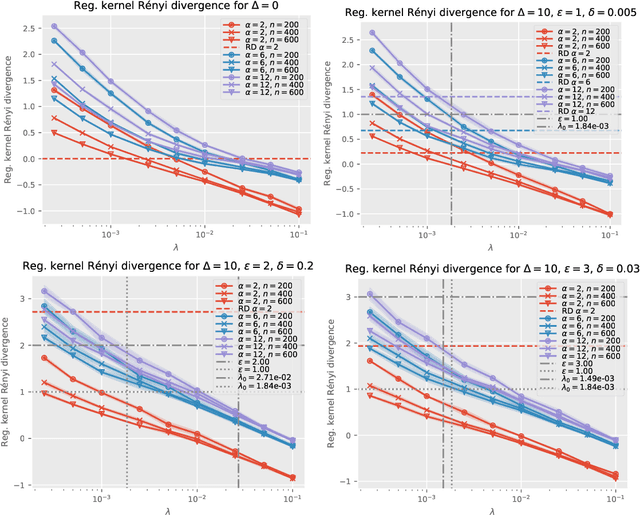
Differential privacy (DP) is the de facto standard for private data release and private machine learning. Auditing black-box DP algorithms and mechanisms to certify whether they satisfy a certain DP guarantee is challenging, especially in high dimension. We propose relaxations of differential privacy based on new divergences on probability distributions: the kernel R\'enyi divergence and its regularized version. We show that the regularized kernel R\'enyi divergence can be estimated from samples even in high dimensions, giving rise to auditing procedures for $\varepsilon$-DP, $(\varepsilon,\delta)$-DP and $(\alpha,\varepsilon)$-R\'enyi DP.

Learning with Stochastic Orders

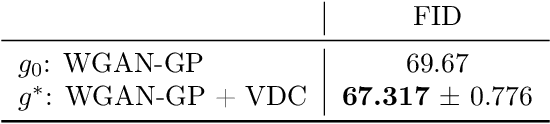
Learning high-dimensional distributions is often done with explicit likelihood modeling or implicit modeling via minimizing integral probability metrics (IPMs). In this paper, we expand this learning paradigm to stochastic orders, namely, the convex or Choquet order between probability measures. Towards this end, we introduce the Choquet-Toland distance between probability measures, that can be used as a drop-in replacement for IPMs. We also introduce the Variational Dominance Criterion (VDC) to learn probability measures with dominance constraints, that encode the desired stochastic order between the learned measure and a known baseline. We analyze both quantities and show that they suffer from the curse of dimensionality and propose surrogates via input convex maxout networks (ICMNs), that enjoy parametric rates. Finally, we provide a min-max framework for learning with stochastic orders and validate it experimentally on synthetic and high-dimensional image generation, with promising results. The code is available at https://github.com/yair-schiff/stochastic-orders-ICMN

Cycle Consistent Probability Divergences Across Different Spaces

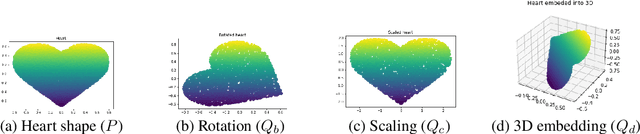
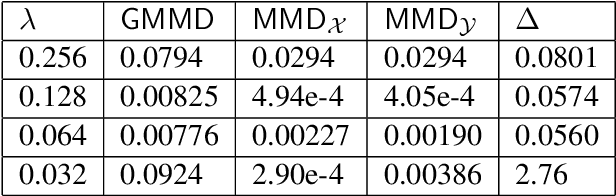
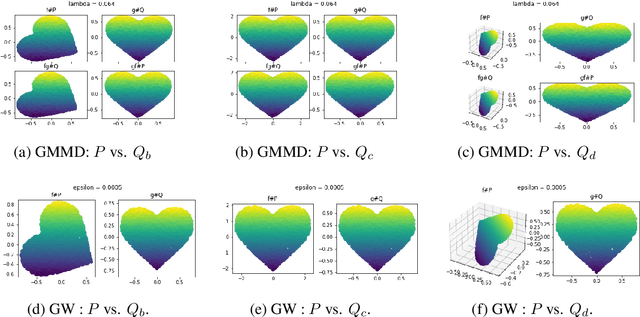
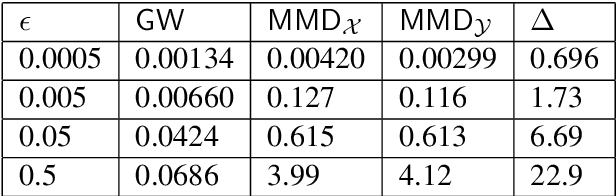
Discrepancy measures between probability distributions are at the core of statistical inference and machine learning. In many applications, distributions of interest are supported on different spaces, and yet a meaningful correspondence between data points is desired. Motivated to explicitly encode consistent bidirectional maps into the discrepancy measure, this work proposes a novel unbalanced Monge optimal transport formulation for matching, up to isometries, distributions on different spaces. Our formulation arises as a principled relaxation of the Gromov-Haussdroff distance between metric spaces, and employs two cycle-consistent maps that push forward each distribution onto the other. We study structural properties of the proposed discrepancy and, in particular, show that it captures the popular cycle-consistent generative adversarial network (GAN) framework as a special case, thereby providing the theory to explain it. Motivated by computational efficiency, we then kernelize the discrepancy and restrict the mappings to parametric function classes. The resulting kernelized version is coined the generalized maximum mean discrepancy (GMMD). Convergence rates for empirical estimation of GMMD are studied and experiments to support our theory are provided.

Physics-enhanced deep surrogates for PDEs

We present a "physics-enhanced deep-surrogate ("PEDS") approach towards developing fast surrogate models for complex physical systems described by partial differential equations (PDEs) and similar models: we show how to combine a low-fidelity "coarse" solver with a neural network that generates "coarsified'' inputs, trained end-to-end to globally match the output of an expensive high-fidelity numerical solver. In this way, by incorporating limited physical knowledge in the form of the low-fidelity model, we find that a PEDS surrogate can be trained with at least $\sim 10\times$ less data than a "black-box'' neural network for the same accuracy. Asymptotically, PEDS appears to learn with a steeper power law than black-box surrogates, and benefits even further when combined with active learning. We demonstrate feasibility and benefit of the proposed approach by using an example problem in electromagnetic scattering that appears in the design of optical metamaterials.

Tighter Sparse Approximation Bounds for ReLU Neural Networks

A well-known line of work (Barron, 1993; Breiman, 1993; Klusowski & Barron, 2018) provides bounds on the width $n$ of a ReLU two-layer neural network needed to approximate a function $f$ over the ball $\mathcal{B}_R(\R^d)$ up to error $\epsilon$, when the Fourier based quantity $C_f = \int_{\R^d} \|\xi\|^2 |\hat{f}(\xi)| \ d\xi$ is finite. More recently Ongie et al. (2019) used the Radon transform as a tool for analysis of infinite-width ReLU two-layer networks. In particular, they introduce the concept of Radon-based $\mathcal{R}$-norms and show that a function defined on $\R^d$ can be represented as an infinite-width two-layer neural network if and only if its $\mathcal{R}$-norm is finite. In this work, we extend the framework of Ongie et al. (2019) and define similar Radon-based semi-norms ($\mathcal{R}, \mathcal{U}$-norms) such that a function admits an infinite-width neural network representation on a bounded open set $\mathcal{U} \subseteq \R^d$ when its $\mathcal{R}, \mathcal{U}$-norm is finite. Building on this, we derive sparse (finite-width) neural network approximation bounds that refine those of Breiman (1993); Klusowski & Barron (2018). Finally, we show that infinite-width neural network representations on bounded open sets are not unique and study their structure, providing a functional view of mode connectivity.

Separation Results between Fixed-Kernel and Feature-Learning Probability Metrics

Several works in implicit and explicit generative modeling empirically observed that feature-learning discriminators outperform fixed-kernel discriminators in terms of the sample quality of the models. We provide separation results between probability metrics with fixed-kernel and feature-learning discriminators using the function classes $\mathcal{F}_2$ and $\mathcal{F}_1$ respectively, which were developed to study overparametrized two-layer neural networks. In particular, we construct pairs of distributions over hyper-spheres that can not be discriminated by fixed kernel $(\mathcal{F}_2)$ integral probability metric (IPM) and Stein discrepancy (SD) in high dimensions, but that can be discriminated by their feature learning ($\mathcal{F}_1$) counterparts. To further study the separation we provide links between the $\mathcal{F}_1$ and $\mathcal{F}_2$ IPMs with sliced Wasserstein distances. Our work suggests that fixed-kernel discriminators perform worse than their feature learning counterparts because their corresponding metrics are weaker.

Do Large Scale Molecular Language Representations Capture Important Structural Information?

Predicting chemical properties from the structure of a molecule is of great importance in many applications including drug discovery and material design. Machine learning based molecular property prediction holds the promise of enabling accurate predictions at much less complexity, when compared to, for example Density Functional Theory (DFT) calculations. Features extracted from molecular graphs, using graph neural nets in a supervised manner, have emerged as strong baselines for such tasks. However, the vast chemical space together with the limited availability of labels makes supervised learning challenging, calling for learning a general-purpose molecular representation. Recently, pre-trained transformer-based language models (PTLMs) on large unlabeled corpus have produced state-of-the-art results in many downstream natural language processing tasks. Inspired by this development, here we present molecular embeddings obtained by training an efficient transformer encoder model, referred to as MoLFormer. This model was employed with a linear attention mechanism and highly paralleized training on 1D SMILES sequences of 1.1 billion unlabeled molecules from the PubChem and ZINC datasets. Experiments show that the learned molecular representation performs competitively, when compared to existing graph-based and fingerprint-based supervised learning baselines, on the challenging tasks of predicting properties of QM8 and QM9 molecules. Further task-specific fine-tuning of the MoLFormerr representation improves performance on several of those property prediction benchmarks. These results provide encouraging evidence that large-scale molecular language models can capture sufficient structural information to be able to accurately predict quantum chemical properties and beyond.

Optimizing Functionals on the Space of Probabilities with Input Convex Neural Networks

Gradient flows are a powerful tool for optimizing functionals in general metric spaces, including the space of probabilities endowed with the Wasserstein metric. A typical approach to solving this optimization problem relies on its connection to the dynamic formulation of optimal transport and the celebrated Jordan-Kinderlehrer-Otto (JKO) scheme. However, this formulation involves optimization over convex functions, which is challenging, especially in high dimensions. In this work, we propose an approach that relies on the recently introduced input-convex neural networks (ICNN) to parameterize the space of convex functions in order to approximate the JKO scheme, as well as in designing functionals over measures that enjoy convergence guarantees. We derive a computationally efficient implementation of this JKO-ICNN framework and use various experiments to demonstrate its feasibility and validity in approximating solutions of low-dimensional partial differential equations with known solutions. We also explore the use of our JKO-ICNN approach in high dimensions with an experiment in controlled generation for molecular discovery.