Quantum Verifiable Rewards for Post-Training Qiskit Code Assistant

Qiskit is an open-source quantum computing framework that allows users to design, simulate, and run quantum circuits on real quantum hardware. We explore post-training techniques for LLMs to assist in writing Qiskit code. We introduce quantum verification as an effective method for ensuring code quality and executability on quantum hardware. To support this, we developed a synthetic data pipeline that generates quantum problem-unit test pairs and used it to create preference data for aligning LLMs with DPO. Additionally, we trained models using GRPO, leveraging quantum-verifiable rewards provided by the quantum hardware. Our best-performing model, combining DPO and GRPO, surpasses the strongest open-source baselines on the challenging Qiskit-HumanEval-hard benchmark.

GP-MoLFormer-Sim: Test Time Molecular Optimization through Contextual Similarity Guidance

The ability to design molecules while preserving similarity to a target molecule and/or property is crucial for various applications in drug discovery, chemical design, and biology. We introduce in this paper an efficient training-free method for navigating and sampling from the molecular space with a generative Chemical Language Model (CLM), while using the molecular similarity to the target as a guide. Our method leverages the contextual representations learned from the CLM itself to estimate the molecular similarity, which is then used to adjust the autoregressive sampling strategy of the CLM. At each step of the decoding process, the method tracks the distance of the current generations from the target and updates the logits to encourage the preservation of similarity in generations. We implement the method using a recently proposed $\sim$47M parameter SMILES-based CLM, GP-MoLFormer, and therefore refer to the method as GP-MoLFormer-Sim, which enables a test-time update of the deep generative policy to reflect the contextual similarity to a set of guide molecules. The method is further integrated into a genetic algorithm (GA) and tested on a set of standard molecular optimization benchmarks involving property optimization, molecular rediscovery, and structure-based drug design. Results show that, GP-MoLFormer-Sim, combined with GA (GP-MoLFormer-Sim+GA) outperforms existing training-free baseline methods, when the oracle remains black-box. The findings in this work are a step forward in understanding and guiding the generative mechanisms of CLMs.

Guided Speculative Inference for Efficient Test-Time Alignment of LLMs

We propose Guided Speculative Inference (GSI), a novel algorithm for efficient reward-guided decoding in large language models. GSI combines soft best-of-$n$ test-time scaling with a reward model $r(x,y)$ and speculative samples from a small auxiliary model $\pi_S(y\mid x)$. We provably approximate the optimal tilted policy $\pi_{\beta,B}(y\mid x) \propto \pi_B(y\mid x)\exp(\beta\,r(x,y))$ of soft best-of-$n$ under the primary model $\pi_B$. We derive a theoretical bound on the KL divergence between our induced distribution and the optimal policy. In experiments on reasoning benchmarks (MATH500, OlympiadBench, Minerva Math), our method achieves higher accuracy than standard soft best-of-$n$ with $\pi_S$ and reward-guided speculative decoding (Liao et al., 2025), and in certain settings even outperforms soft best-of-$n$ with $\pi_B$. The code is available at https://github.com/j-geuter/GSI .

Revisiting Group Relative Policy Optimization: Insights into On-Policy and Off-Policy Training

We revisit Group Relative Policy Optimization (GRPO) in both on-policy and off-policy optimization regimes. Our motivation comes from recent work on off-policy Proximal Policy Optimization (PPO), which improves training stability, sampling efficiency, and memory usage. In addition, a recent analysis of GRPO suggests that estimating the advantage function with off-policy samples could be beneficial. Building on these observations, we adapt GRPO to the off-policy setting. We show that both on-policy and off-policy GRPO objectives yield an improvement in the reward. This result motivates the use of clipped surrogate objectives in the off-policy version of GRPO. We then compare the empirical performance of reinforcement learning with verifiable rewards in post-training using both GRPO variants. Our results show that off-policy GRPO either significantly outperforms or performs on par with its on-policy counterpart.

Reinforcement Learning with Verifiable Rewards: GRPO's Effective Loss, Dynamics, and Success Amplification

Group Relative Policy Optimization (GRPO) was introduced and used successfully to train DeepSeek R1 models for promoting reasoning capabilities of LLMs using verifiable or binary rewards. We show in this paper that GRPO with verifiable rewards can be written as a Kullback Leibler ($\mathsf{KL}$) regularized contrastive loss, where the contrastive samples are synthetic data sampled from the old policy. The optimal GRPO policy $\pi_{n}$ can be expressed explicitly in terms of the binary reward, as well as the first and second order statistics of the old policy ($\pi_{n-1}$) and the reference policy $\pi_0$. Iterating this scheme, we obtain a sequence of policies $\pi_{n}$ for which we can quantify the probability of success $p_n$. We show that the probability of success of the policy satisfies a recurrence that converges to a fixed point of a function that depends on the initial probability of success $p_0$ and the regularization parameter $\beta$ of the $\mathsf{KL}$ regularizer. We show that the fixed point $p^*$ is guaranteed to be larger than $p_0$, thereby demonstrating that GRPO effectively amplifies the probability of success of the policy.

Verify when Uncertain: Beyond Self-Consistency in Black Box Hallucination Detection

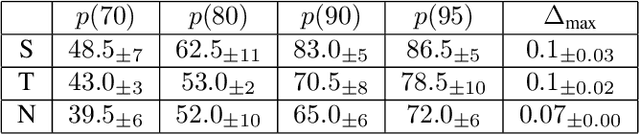
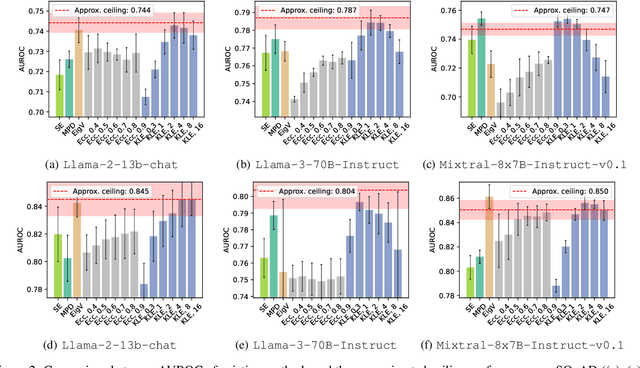
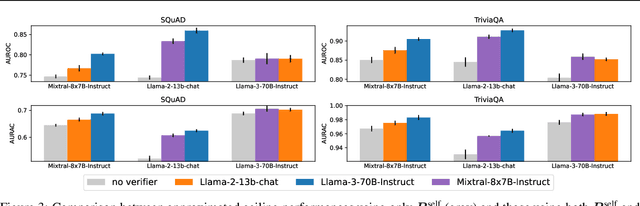
Large Language Models (LLMs) suffer from hallucination problems, which hinder their reliability in sensitive applications. In the black-box setting, several self-consistency-based techniques have been proposed for hallucination detection. We empirically study these techniques and show that they achieve performance close to that of a supervised (still black-box) oracle, suggesting little room for improvement within this paradigm. To address this limitation, we explore cross-model consistency checking between the target model and an additional verifier LLM. With this extra information, we observe improved oracle performance compared to purely self-consistency-based methods. We then propose a budget-friendly, two-stage detection algorithm that calls the verifier model only for a subset of cases. It dynamically switches between self-consistency and cross-consistency based on an uncertainty interval of the self-consistency classifier. We provide a geometric interpretation of consistency-based hallucination detection methods through the lens of kernel mean embeddings, offering deeper theoretical insights. Extensive experiments show that this approach maintains high detection performance while significantly reducing computational cost.

Theoretical Analysis of KL-regularized RLHF with Multiple Reference Models

Recent methods for aligning large language models (LLMs) with human feedback predominantly rely on a single reference model, which limits diversity, model overfitting, and underutilizes the wide range of available pre-trained models. Incorporating multiple reference models has the potential to address these limitations by broadening perspectives, reducing bias, and leveraging the strengths of diverse open-source LLMs. However, integrating multiple reference models into reinforcement learning with human feedback (RLHF) frameworks poses significant theoretical challenges, particularly in reverse KL-regularization, where achieving exact solutions has remained an open problem. This paper presents the first \emph{exact solution} to the multiple reference model problem in reverse KL-regularized RLHF. We introduce a comprehensive theoretical framework that includes rigorous statistical analysis and provides sample complexity guarantees. Additionally, we extend our analysis to forward KL-regularized RLHF, offering new insights into sample complexity requirements in multiple reference scenarios. Our contributions lay the foundation for more advanced and adaptable LLM alignment techniques, enabling the effective use of multiple reference models. This work paves the way for developing alignment frameworks that are both theoretically sound and better suited to the challenges of modern AI ecosystems.

Large Language Models can be Strong Self-Detoxifiers

Reducing the likelihood of generating harmful and toxic output is an essential task when aligning large language models (LLMs). Existing methods mainly rely on training an external reward model (i.e., another language model) or fine-tuning the LLM using self-generated data to influence the outcome. In this paper, we show that LLMs have the capability of self-detoxification without the use of an additional reward model or re-training. We propose \textit{Self-disciplined Autoregressive Sampling (SASA)}, a lightweight controlled decoding algorithm for toxicity reduction of LLMs. SASA leverages the contextual representations from an LLM to learn linear subspaces characterizing toxic v.s. non-toxic output in analytical forms. When auto-completing a response token-by-token, SASA dynamically tracks the margin of the current output to steer the generation away from the toxic subspace, by adjusting the autoregressive sampling strategy. Evaluated on LLMs of different scale and nature, namely Llama-3.1-Instruct (8B), Llama-2 (7B), and GPT2-L models with the RealToxicityPrompts, BOLD, and AttaQ benchmarks, SASA markedly enhances the quality of the generated sentences relative to the original models and attains comparable performance to state-of-the-art detoxification techniques, significantly reducing the toxicity level by only using the LLM's internal representations.

Gradient Flows and Riemannian Structure in the Gromov-Wasserstein Geometry

The Wasserstein space of probability measures is known for its intricate Riemannian structure, which underpins the Wasserstein geometry and enables gradient flow algorithms. However, the Wasserstein geometry may not be suitable for certain tasks or data modalities. Motivated by scenarios where the global structure of the data needs to be preserved, this work initiates the study of gradient flows and Riemannian structure in the Gromov-Wasserstein (GW) geometry, which is particularly suited for such purposes. We focus on the inner product GW (IGW) distance between distributions on $\mathbb{R}^d$. Given a functional $\mathsf{F}:\mathcal{P}_2(\mathbb{R}^d)\to\mathbb{R}$ to optimize, we present an implicit IGW minimizing movement scheme that generates a sequence of distributions $\{\rho_i\}_{i=0}^n$, which are close in IGW and aligned in the 2-Wasserstein sense. Taking the time step to zero, we prove that the discrete solution converges to an IGW generalized minimizing movement (GMM) $(\rho_t)_t$ that follows the continuity equation with a velocity field $v_t\in L^2(\rho_t;\mathbb{R}^d)$, specified by a global transformation of the Wasserstein gradient of $\mathsf{F}$. The transformation is given by a mobility operator that modifies the Wasserstein gradient to encode not only local information, but also global structure. Our gradient flow analysis leads us to identify the Riemannian structure that gives rise to the intrinsic IGW geometry, using which we establish a Benamou-Brenier-like formula for IGW. We conclude with a formal derivation, akin to the Otto calculus, of the IGW gradient as the inverse mobility acting on the Wasserstein gradient. Numerical experiments validating our theory and demonstrating the global nature of IGW interpolations are provided.

Multivariate Stochastic Dominance via Optimal Transport and Applications to Models Benchmarking

Stochastic dominance is an important concept in probability theory, econometrics and social choice theory for robustly modeling agents' preferences between random outcomes. While many works have been dedicated to the univariate case, little has been done in the multivariate scenario, wherein an agent has to decide between different multivariate outcomes. By exploiting a characterization of multivariate first stochastic dominance in terms of couplings, we introduce a statistic that assesses multivariate almost stochastic dominance under the framework of Optimal Transport with a smooth cost. Further, we introduce an entropic regularization of this statistic, and establish a central limit theorem (CLT) and consistency of the bootstrap procedure for the empirical statistic. Armed with this CLT, we propose a hypothesis testing framework as well as an efficient implementation using the Sinkhorn algorithm. We showcase our method in comparing and benchmarking Large Language Models that are evaluated on multiple metrics. Our multivariate stochastic dominance test allows us to capture the dependencies between the metrics in order to make an informed and statistically significant decision on the relative performance of the models.