Near Instance Optimal Model Selection for Pure Exploration Linear Bandits

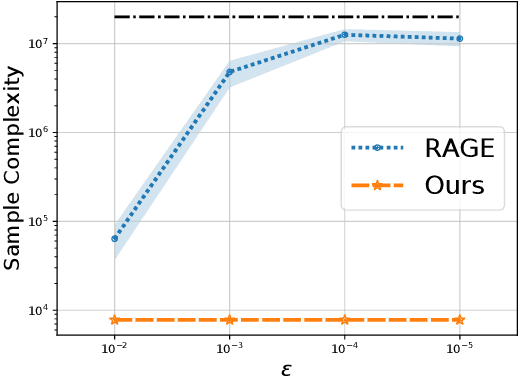
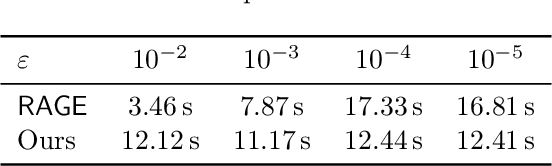
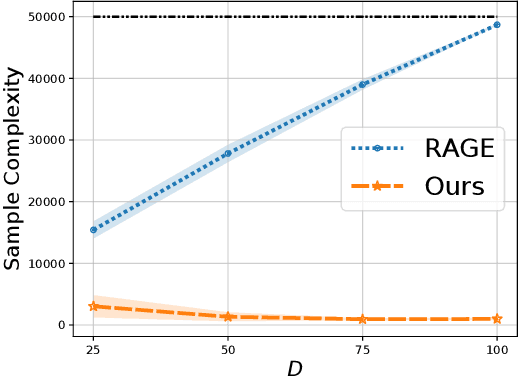
The model selection problem in the pure exploration linear bandit setting is introduced and studied in both the fixed confidence and fixed budget settings. The model selection problem considers a nested sequence of hypothesis classes of increasing complexities. Our goal is to automatically adapt to the instance-dependent complexity measure of the smallest hypothesis class containing the true model, rather than suffering from the complexity measure related to the largest hypothesis class. We provide evidence showing that a standard doubling trick over dimension fails to achieve the optimal instance-dependent sample complexity. Our algorithms define a new optimization problem based on experimental design that leverages the geometry of the action set to efficiently identify a near-optimal hypothesis class. Our fixed budget algorithm uses a novel application of a selection-validation trick in bandits. This provides a new method for the understudied fixed budget setting in linear bandits (even without the added challenge of model selection). We further generalize the model selection problem to the misspecified regime, adapting our algorithms in both fixed confidence and fixed budget settings.

Pure Exploration in Kernel and Neural Bandits

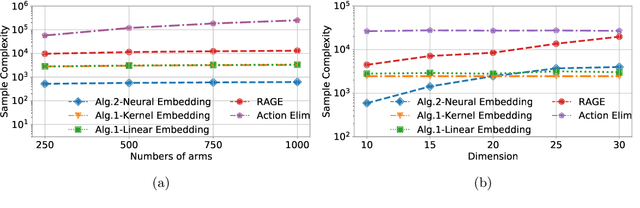
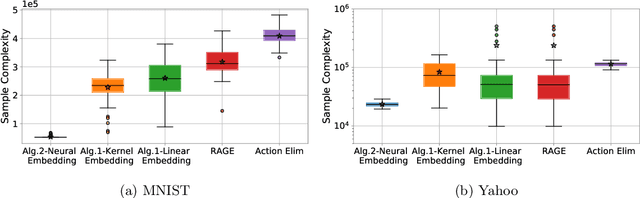
We study pure exploration in bandits, where the dimension of the feature representation can be much larger than the number of arms. To overcome the curse of dimensionality, we propose to adaptively embed the feature representation of each arm into a lower-dimensional space and carefully deal with the induced model misspecifications. Our approach is conceptually very different from existing works that can either only handle low-dimensional linear bandits or passively deal with model misspecifications. We showcase the application of our approach to two pure exploration settings that were previously under-studied: (1) the reward function belongs to a possibly infinite-dimensional Reproducing Kernel Hilbert Space, and (2) the reward function is nonlinear and can be approximated by neural networks. Our main results provide sample complexity guarantees that only depend on the effective dimension of the feature spaces in the kernel or neural representations. Extensive experiments conducted on both synthetic and real-world datasets demonstrate the efficacy of our methods.

Pareto Optimal Model Selection in Linear Bandits

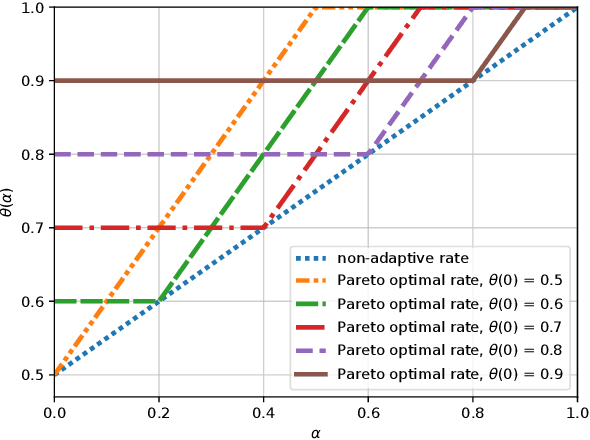
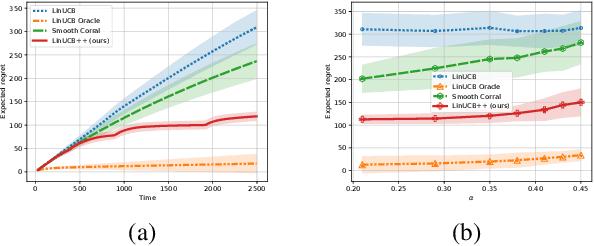
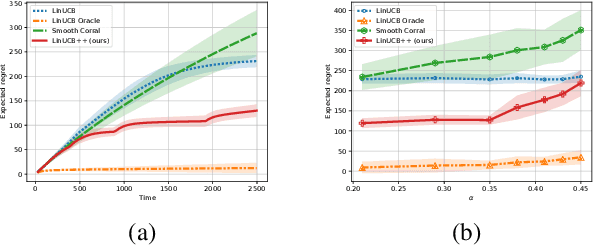
We study a model selection problem in the linear bandit setting, where the learner must adapt to the dimension of the optimal hypothesis class on the fly and balance exploration and exploitation. More specifically, we assume a sequence of nested linear hypothesis classes with dimensions $d_1 < d_2 < \dots$, and the goal is to automatically adapt to the smallest hypothesis class that contains the true linear model. Although previous papers provide various guarantees for this model selection problem, the analysis therein either works in favorable cases when one can cheaply conduct statistical testing to locate the right hypothesis class or is based on the idea of "corralling" multiple base algorithms which often performs relatively poorly in practice. These works also mainly focus on upper bounding the regret. In this paper, we first establish a lower bound showing that, even with a fixed action set, adaptation to the unknown intrinsic dimension $d_\star$ comes at a cost: there is no algorithm that can achieve the regret bound $\widetilde{O}(\sqrt{d_\star T})$ simultaneously for all values of $d_\star$. We also bring new ideas, i.e., constructing virtual mixture-arms to effectively summarize useful information, into the model selection problem in linear bandits. Under a mild assumption on the action set, we design a Pareto optimal algorithm with guarantees matching the rate in the lower bound. Experimental results confirm our theoretical results and show advantages of our algorithm compared to prior work.

Robust Outlier Arm Identification

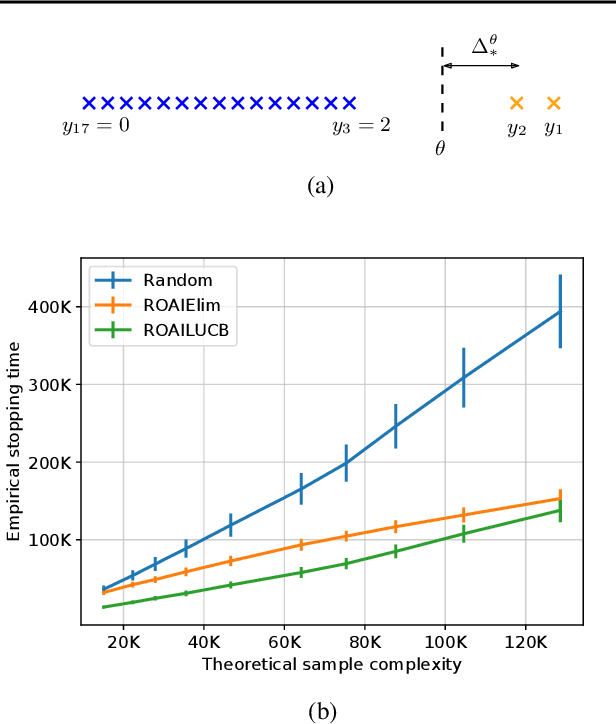
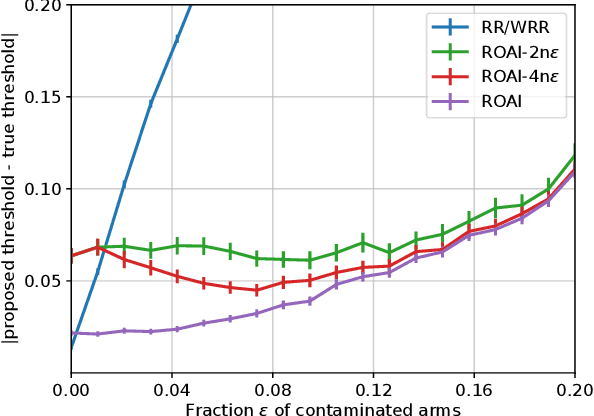
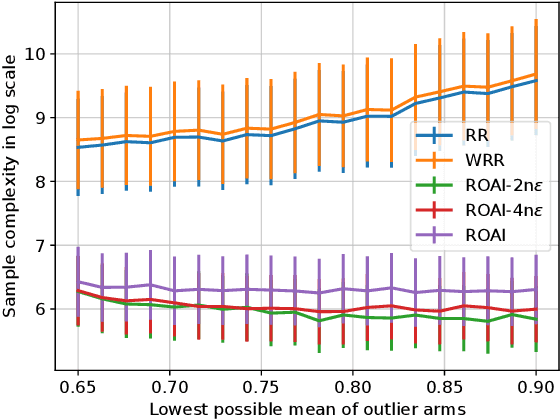
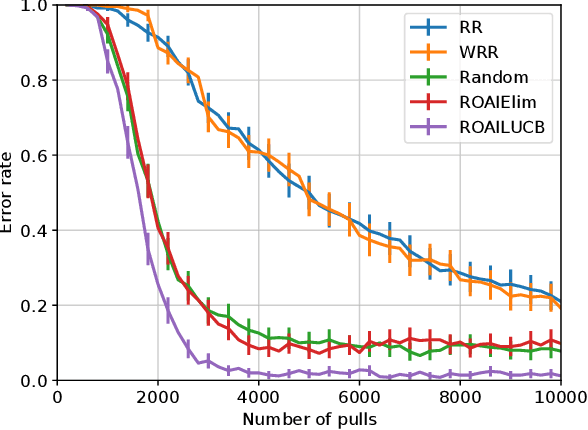
We study the problem of Robust Outlier Arm Identification (ROAI), where the goal is to identify arms whose expected rewards deviate substantially from the majority, by adaptively sampling from their reward distributions. We compute the outlier threshold using the median and median absolute deviation of the expected rewards. This is a robust choice for the threshold compared to using the mean and standard deviation, since it can identify outlier arms even in the presence of extreme outlier values. Our setting is different from existing pure exploration problems where the threshold is pre-specified as a given value or rank. This is useful in applications where the goal is to identify the set of promising items but the cardinality of this set is unknown, such as finding promising drugs for a new disease or identifying items favored by a population. We propose two $\delta$-PAC algorithms for ROAI, which includes the first UCB-style algorithm for outlier detection, and derive upper bounds on their sample complexity. We also prove a matching, up to logarithmic factors, worst case lower bound for the problem, indicating that our upper bounds are generally unimprovable. Experimental results show that our algorithms are both robust and about $5$x sample efficient compared to state-of-the-art.

On Regret with Multiple Best Arms

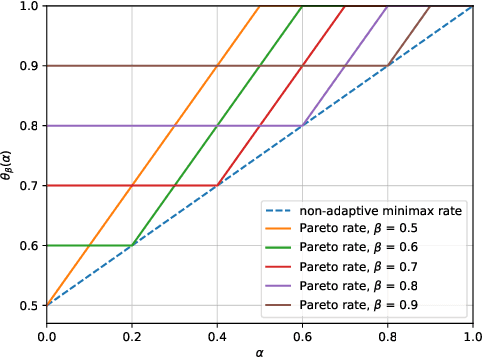
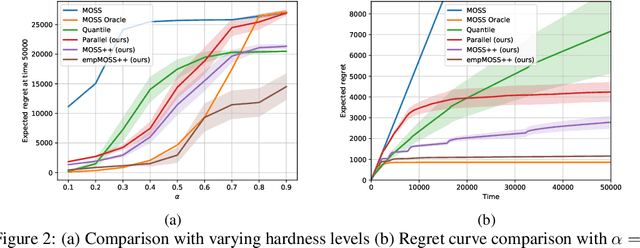
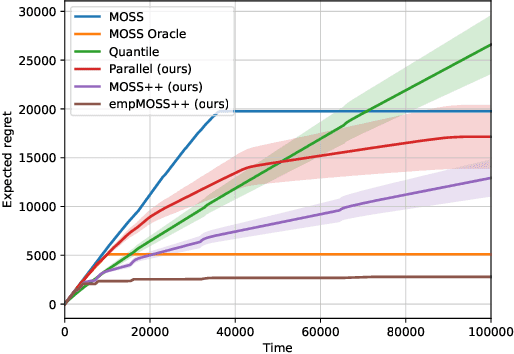
We study regret minimization problem with the existence of multiple best/near-optimal arms in the multi-armed bandit setting. We consider the case where the number of arms/actions is comparable or much larger than the time horizon, and make no assumptions about the structure of the bandit instance. Our goal is to design algorithms that can automatically adapt to the unknown hardness of the problem, i.e., the number of best arms. Our setting captures many modern applications of bandit algorithms where the action space is enormous and the information about the underlying instance/structure is unavailable. We first propose an adaptive algorithm that is agnostic to the hardness level and theoretically derive its regret bound. We then prove a lower bound for our problem setting, which indicates: (1) no algorithm can be optimal simultaneously over all hardness levels; and (2) our algorithm achieves an adaptive rate function that is Pareto optimal. With additional knowledge of the expected reward of the best arm, we propose another adaptive algorithm that is minimax optimal, up to polylog factors, over all hardness levels. Experimental results confirm our theoretical guarantees and show advantages of our algorithms over the previous state-of-the-art.

ReabsNet: Detecting and Revising Adversarial Examples

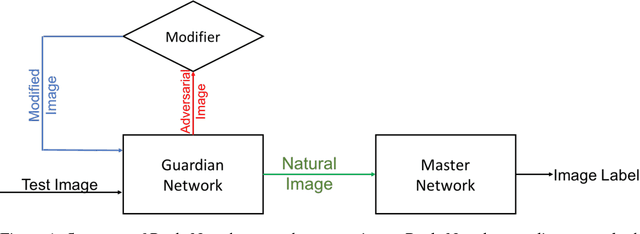
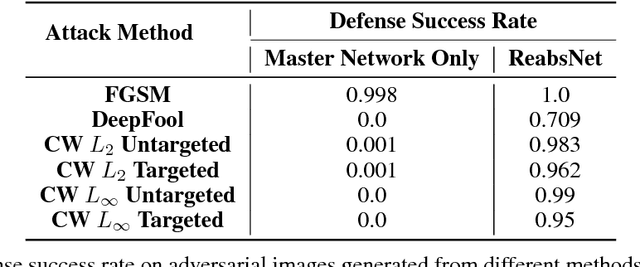
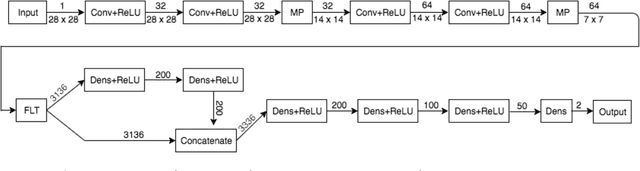
Though deep neural network has hit a huge success in recent studies and applica- tions, it still remains vulnerable to adversarial perturbations which are imperceptible to humans. To address this problem, we propose a novel network called ReabsNet to achieve high classification accuracy in the face of various attacks. The approach is to augment an existing classification network with a guardian network to detect if a sample is natural or has been adversarially perturbed. Critically, instead of simply rejecting adversarial examples, we revise them to get their true labels. We exploit the observation that a sample containing adversarial perturbations has a possibility of returning to its true class after revision. We demonstrate that our ReabsNet outperforms the state-of-the-art defense method under various adversarial attacks.