Expressivity of Transformers: A Tropical Geometry Perspective

To quantify the geometric expressivity of transformers, we introduce a tropical geometry framework to characterize their exact spatial partitioning capabilities. By modeling self-attention as a vector-valued tropical rational map, we prove it evaluates exactly to a Power Voronoi Diagram in the zero-temperature limit. Building on this equivalence, we establish a combinatorial rationale for Multi-Head Self-Attention (MHSA): via the Minkowski sum of Newton polytopes, multi-head aggregation expands the polyhedral complexity to $\mathcal{O}(N^H)$, overcoming the $\mathcal{O}(N)$ bottleneck of single heads. Extending this to deep architectures, we derive the first tight asymptotic bounds on the number of linear regions in transformers ($Θ(N^{d_{\text{model}}L})$), demonstrating a combinatorial explosion driven intrinsically by sequence length $N$, ambient embedding dimension $d_{\text{model}}$, and network depth $L$. Importantly, we guarantee that this idealized polyhedral skeleton is geometrically stable: finite-temperature soft attention preserves these topological partitions via exponentially tight differential approximation bounds.

Exact Finite-Sample Variance Decomposition of Subagging: A Spectral Filtering Perspective

Standard resampling ratios (e.g., $α\approx 0.632$) are widely used as default baselines in ensemble learning for three decades. However, how these ratios interact with a base learner's intrinsic functional complexity in finite samples lacks a exact mathematical characterization. We leverage the Hoeffding-ANOVA decomposition to derive the first exact, finite-sample variance decomposition for subagging, applicable to any symmetric base learner without requiring asymptotic limits or smoothness assumptions. We establish that subagging operates as a deterministic low-pass spectral filter: it preserves low-order structural signals while attenuating $c$-th order interaction variance by a geometric factor approaching $α^c$. This decoupling reveals why default baselines often under-regularize high-capacity interpolators, which instead require smaller $α$ to exponentially suppress spurious high-order noise. To operationalize these insights, we propose a complexity-guided adaptive subsampling algorithm, empirically demonstrating that dynamically calibrating $α$ to the learner's complexity spectrum consistently improves generalization over static baselines.

Sparsity is Combinatorial Depth: Quantifying MoE Expressivity via Tropical Geometry

While Mixture-of-Experts (MoE) architectures define the state-of-the-art, their theoretical success is often attributed to heuristic efficiency rather than geometric expressivity. In this work, we present the first analysis of MoE through the lens of tropical geometry, establishing that the Top-$k$ routing mechanism is algebraically isomorphic to the $k$-th elementary symmetric tropical polynomial. This isomorphism partitions the input space into the Normal Fan of a Hypersimplex, revealing that \textbf{sparsity is combinatorial depth} which scales geometric capacity by the binomial coefficient $\binom{N}{k}$. Moving beyond ambient bounds, we introduce the concept of \textit{Effective Capacity} under the Manifold Hypothesis. We prove that while dense networks suffer from capacity collapse on low-dimensional data, MoE architectures exhibit \textit{Combinatorial Resilience}, maintaining high expressivity via the transversality of routing cones. In this study, our framework unifies the discrete geometry of the Hypersimplex with the continuous geometry of neural functions, offering a rigorous theoretical justification for the topological supremacy of conditional computation.

Effective Frontiers: A Unification of Neural Scaling Laws

Neural scaling laws govern the prediction power-law improvement of test loss with respect to model capacity ($N$), datasize ($D$), and compute ($C$). However, existing theoretical explanations often rely on specific architectures or complex kernel methods, lacking intuitive universality. In this paper, we propose a unified framework that abstracts general learning tasks as the progressive coverage of patterns from a long-tail (Zipfian) distribution. We introduce the Effective Frontier ($k_\star$), a threshold in the pattern rank space that separates learned knowledge from the unlearned tail. We prove that reducible loss is asymptotically determined by the probability mass of the tail a resource-dependent frontier truncation. Based on our framework, we derive the precise scaling laws for $N$, $D$, and $C$, attributing them to capacity, coverage, and optimization bottlenecks, respectively. Furthermore, we unify these mechanisms via a Max-Bottleneck principle, demonstrating that the Kaplan and Chinchilla scaling laws are not contradictory, but equilibrium solutions to the same constrained optimization problem under different active bottlenecks.

Variational Inference, Entropy, and Orthogonality: A Unified Theory of Mixture-of-Experts

Mixture-of-Experts models enable large language models to scale efficiently, as they only activate a subset of experts for each input. Their core mechanisms, Top-k routing and auxiliary load balancing, remain heuristic, however, lacking a cohesive theoretical underpinning to support them. To this end, we build the first unified theoretical framework that rigorously derives these practices as optimal sparse posterior approximation and prior regularization from a Bayesian perspective, while simultaneously framing them as mechanisms to minimize routing ambiguity and maximize channel capacity from an information-theoretic perspective. We also pinpoint the inherent combinatorial hardness of routing, defining it as the NP-hard sparse subset selection problem. We rigorously prove the existence of a "Coherence Barrier"; when expert representations exhibit high mutual coherence, greedy routing strategies theoretically fail to recover the optimal expert subset. Importantly, we formally verify that imposing geometric orthogonality in the expert feature space is sufficient to narrow the divide between the NP-hard global optimum and polynomial-time greedy approximation. Our comparative analyses confirm orthogonality regularization as the optimal engineering relaxation for large-scale models. Our work offers essential theoretical support and technical assurance for a deeper understanding and novel designs of MoE.

Temporal Gaussian Copula For Clinical Multivariate Time Series Data Imputation

The imputation of the Multivariate time series (MTS) is particularly challenging since the MTS typically contains irregular patterns of missing values due to various factors such as instrument failures, interference from irrelevant data, and privacy regulations. Existing statistical methods and deep learning methods have shown promising results in time series imputation. In this paper, we propose a Temporal Gaussian Copula Model (TGC) for three-order MTS imputation. The key idea is to leverage the Gaussian Copula to explore the cross-variable and temporal relationships based on the latent Gaussian representation. Subsequently, we employ an Expectation-Maximization (EM) algorithm to improve robustness in managing data with varying missing rates. Comprehensive experiments were conducted on three real-world MTS datasets. The results demonstrate that our TGC substantially outperforms the state-of-the-art imputation methods. Additionally, the TGC model exhibits stronger robustness to the varying missing ratios in the test dataset. Our code is available at https://github.com/MVL-Lab/TGC-MTS.

Signal Acquisition of Luojia-1A Low Earth Orbit Navigation Augmentation System with Software Defined Receiver

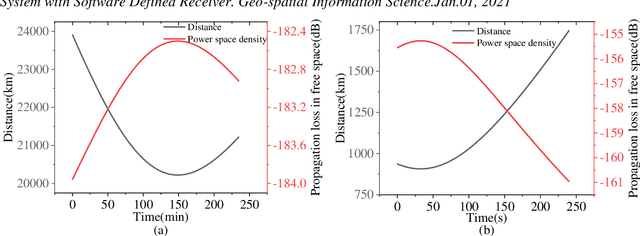
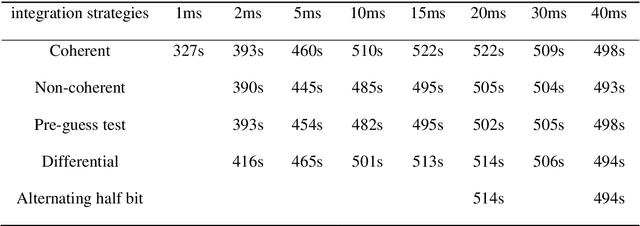
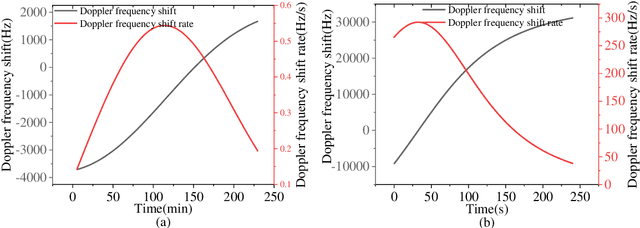
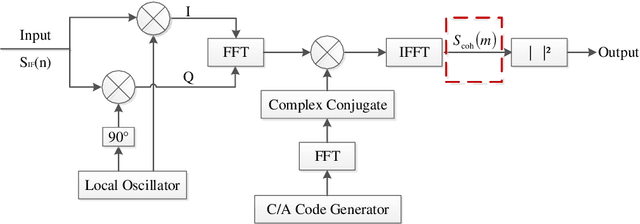
Low earth orbit (LEO) satellite navigation signal can be used as an opportunity signal in case of a Global navigation satellite system (GNSS) outage, or as an enhancement means of traditional GNSS positioning algorithms. No matter which service mode is used, signal acquisition is the prerequisite of providing enhanced LEO navigation service. Compared with the medium orbit satellite, the transit time of the LEO satellite is shorter. Thus, it is of great significance to expand the successful acquisition time range of the LEO signal. Previous studies on LEO signal acquisition are based on simulation data. However, signal acquisition research based on real data is very important. In this work, the signal characteristics of LEO satellite: power space density in free space and the Doppler shift of LEO satellite are individually studied. The unified symbol definitions of several integration algorithms based on the parallel search signal acquisition algorithm are given. To verify these algorithms for LEO signal acquisition, a software-defined receiver (SDR) is developed. The performance of those integration algorithms on expanding the successful acquisition time range is verified by the real data collected from the Luojia-1A satellite. The experimental results show that the integration strategy can expand the successful acquisition time range, and it will not expand indefinitely with the integration duration.