Finer Behavioral Foundation Models via Auto-Regressive Features and Advantage Weighting

The forward-backward representation (FB) is a recently proposed framework (Touati et al., 2023; Touati & Ollivier, 2021) to train behavior foundation models (BFMs) that aim at providing zero-shot efficient policies for any new task specified in a given reinforcement learning (RL) environment, without training for each new task. Here we address two core limitations of FB model training. First, FB, like all successor-feature-based methods, relies on a linear encoding of tasks: at test time, each new reward function is linearly projected onto a fixed set of pre-trained features. This limits expressivity as well as precision of the task representation. We break the linearity limitation by introducing auto-regressive features for FB, which let finegrained task features depend on coarser-grained task information. This can represent arbitrary nonlinear task encodings, thus significantly increasing expressivity of the FB framework. Second, it is well-known that training RL agents from offline datasets often requires specific techniques.We show that FB works well together with such offline RL techniques, by adapting techniques from (Nair et al.,2020b; Cetin et al., 2024) for FB. This is necessary to get non-flatlining performance in some datasets, such as DMC Humanoid. As a result, we produce efficient FB BFMs for a number of new environments. Notably, in the D4RL locomotion benchmark, the generic FB agent matches the performance of standard single-task offline agents (IQL, XQL). In many setups, the offline techniques are needed to get any decent performance at all. The auto-regressive features have a positive but moderate impact, concentrated on tasks requiring spatial precision and task generalization beyond the behaviors represented in the trainset.

Simple Ingredients for Offline Reinforcement Learning

Offline reinforcement learning algorithms have proven effective on datasets highly connected to the target downstream task. Yet, leveraging a novel testbed (MOOD) in which trajectories come from heterogeneous sources, we show that existing methods struggle with diverse data: their performance considerably deteriorates as data collected for related but different tasks is simply added to the offline buffer. In light of this finding, we conduct a large empirical study where we formulate and test several hypotheses to explain this failure. Surprisingly, we find that scale, more than algorithmic considerations, is the key factor influencing performance. We show that simple methods like AWAC and IQL with increased network size overcome the paradoxical failure modes from the inclusion of additional data in MOOD, and notably outperform prior state-of-the-art algorithms on the canonical D4RL benchmark.

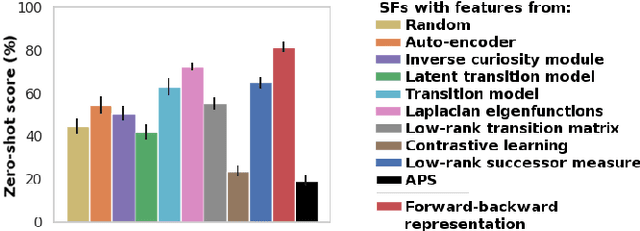
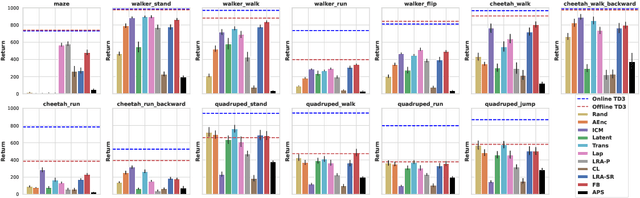
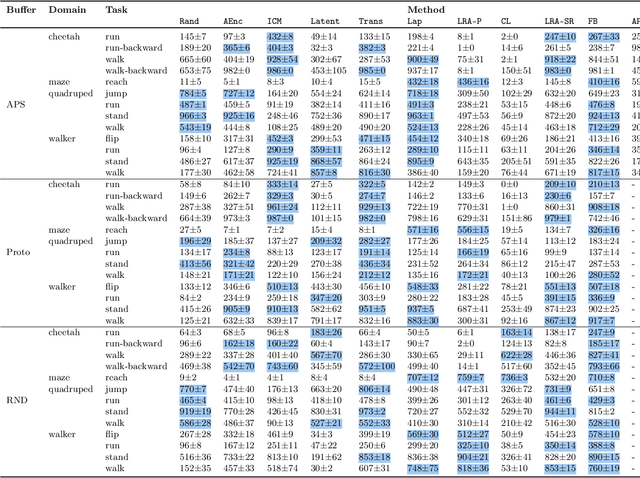
Does Zero-Shot Reinforcement Learning Exist?

A zero-shot RL agent is an agent that can solve any RL task in a given environment, instantly with no additional planning or learning, after an initial reward-free learning phase. This marks a shift from the reward-centric RL paradigm towards "controllable" agents that can follow arbitrary instructions in an environment. Current RL agents can solve families of related tasks at best, or require planning anew for each task. Strategies for approximate zero-shot RL ave been suggested using successor features (SFs) [BBQ+ 18] or forward-backward (FB) representations [TO21], but testing has been limited. After clarifying the relationships between these schemes, we introduce improved losses and new SF models, and test the viability of zero-shot RL schemes systematically on tasks from the Unsupervised RL benchmark [LYL+21]. To disentangle universal representation learning from exploration, we work in an offline setting and repeat the tests on several existing replay buffers. SFs appear to suffer from the choice of the elementary state features. SFs with Laplacian eigenfunctions do well, while SFs based on auto-encoders, inverse curiosity, transition models, low-rank transition matrix, contrastive learning, or diversity (APS), perform unconsistently. In contrast, FB representations jointly learn the elementary and successor features from a single, principled criterion. They perform best and consistently across the board, reaching 85% of supervised RL performance with a good replay buffer, in a zero-shot manner.

Agnostic Physics-Driven Deep Learning

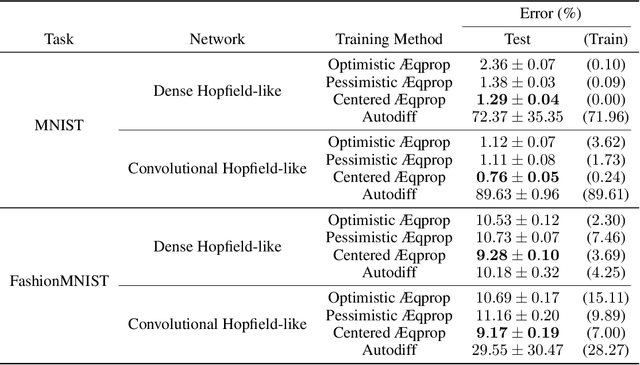
This work establishes that a physical system can perform statistical learning without gradient computations, via an Agnostic Equilibrium Propagation (Aeqprop) procedure that combines energy minimization, homeostatic control, and nudging towards the correct response. In Aeqprop, the specifics of the system do not have to be known: the procedure is based only on external manipulations, and produces a stochastic gradient descent without explicit gradient computations. Thanks to nudging, the system performs a true, order-one gradient step for each training sample, in contrast with order-zero methods like reinforcement or evolutionary strategies, which rely on trial and error. This procedure considerably widens the range of potential hardware for statistical learning to any system with enough controllable parameters, even if the details of the system are poorly known. Aeqprop also establishes that in natural (bio)physical systems, genuine gradient-based statistical learning may result from generic, relatively simple mechanisms, without backpropagation and its requirement for analytic knowledge of partial derivatives.

Unbiased Methods for Multi-Goal Reinforcement Learning

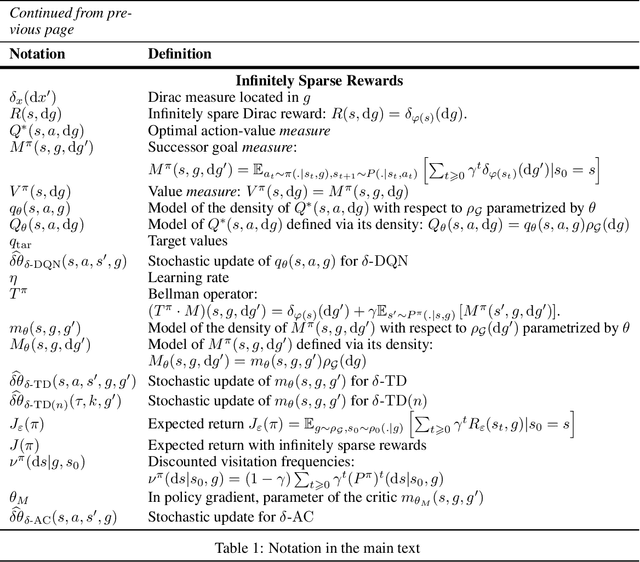
In multi-goal reinforcement learning (RL) settings, the reward for each goal is sparse, and located in a small neighborhood of the goal. In large dimension, the probability of reaching a reward vanishes and the agent receives little learning signal. Methods such as Hindsight Experience Replay (HER) tackle this issue by also learning from realized but unplanned-for goals. But HER is known to introduce bias, and can converge to low-return policies by overestimating chancy outcomes. First, we vindicate HER by proving that it is actually unbiased in deterministic environments, such as many optimal control settings. Next, for stochastic environments in continuous spaces, we tackle sparse rewards by directly taking the infinitely sparse reward limit. We fully formalize the problem of multi-goal RL with infinitely sparse Dirac rewards at each goal. We introduce unbiased deep Q-learning and actor-critic algorithms that can handle such infinitely sparse rewards, and test them in toy environments.

Learning One Representation to Optimize All Rewards

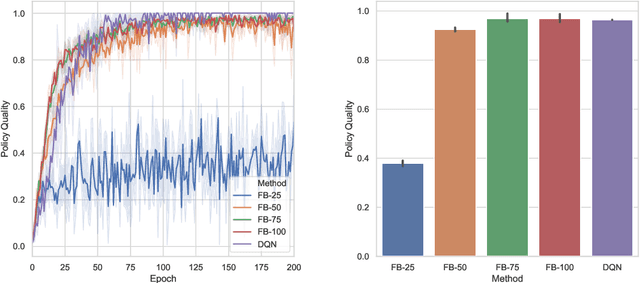
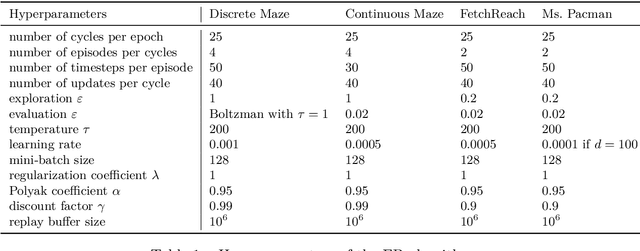
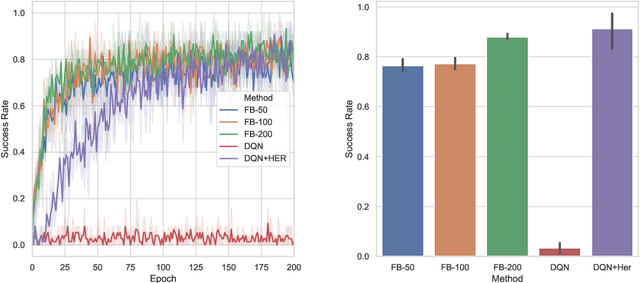
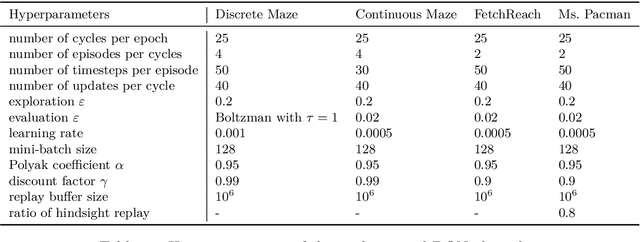
We introduce the forward-backward (FB) representation of the dynamics of a reward-free Markov decision process. It provides explicit near-optimal policies for any reward specified a posteriori. During an unsupervised phase, we use reward-free interactions with the environment to learn two representations via off-the-shelf deep learning methods and temporal difference (TD) learning. In the test phase, a reward representation is estimated either from observations or an explicit reward description (e.g., a target state). The optimal policy for that reward is directly obtained from these representations, with no planning. The unsupervised FB loss is well-principled: if training is perfect, the policies obtained are provably optimal for any reward function. With imperfect training, the sub-optimality is proportional to the unsupervised approximation error. The FB representation learns long-range relationships between states and actions, via a predictive occupancy map, without having to synthesize states as in model-based approaches. This is a step towards learning controllable agents in arbitrary black-box stochastic environments. This approach compares well to goal-oriented RL algorithms on discrete and continuous mazes, pixel-based MsPacman, and the FetchReach virtual robot arm. We also illustrate how the agent can immediately adapt to new tasks beyond goal-oriented RL.

Learning Successor States and Goal-Dependent Values: A Mathematical Viewpoint

In reinforcement learning, temporal difference-based algorithms can be sample-inefficient: for instance, with sparse rewards, no learning occurs until a reward is observed. This can be remedied by learning richer objects, such as a model of the environment, or successor states. Successor states model the expected future state occupancy from any given state for a given policy and are related to goal-dependent value functions, which learn how to reach arbitrary states. We formally derive the temporal difference algorithm for successor state and goal-dependent value function learning, either for discrete or for continuous environments with function approximation. Especially, we provide finite-variance estimators even in continuous environments, where the reward for exactly reaching a goal state becomes infinitely sparse. Successor states satisfy more than just the Bellman equation: a backward Bellman operator and a Bellman-Newton (BN) operator encode path compositionality in the environment. The BN operator is akin to second-order gradient descent methods and provides the true update of the value function when acquiring more observations, with explicit tabular bounds. In the tabular case and with infinitesimal learning rates, mixing the usual and backward Bellman operators provably improves eigenvalues for asymptotic convergence, and the asymptotic convergence of the BN operator is provably better than TD, with a rate independent from the environment. However, the BN method is more complex and less robust to sampling noise. Finally, a forward-backward (FB) finite-rank parameterization of successor states enjoys reduced variance and improved samplability, provides a direct model of the value function, has fully understood fixed points corresponding to long-range dependencies, approximates the BN method, and provides two canonical representations of states as a byproduct.

Convergence of Online Adaptive and Recurrent Optimization Algorithms

We prove local convergence of several notable gradient descentalgorithms used inmachine learning, for which standard stochastic gradient descent theorydoes not apply. This includes, first, online algorithms for recurrent models and dynamicalsystems, such as \emph{Real-time recurrent learning} (RTRL) and its computationally lighter approximations NoBackTrack and UORO; second,several adaptive algorithms such as RMSProp, online natural gradient, and Adam with $\beta^2\to 1$.Despite local convergence being a relatively weak requirement for a newoptimization algorithm, no local analysis was available for these algorithms, as far aswe knew. Analysis of these algorithms does not immediately followfrom standard stochastic gradient (SGD) theory. In fact, Adam has been provedto lack local convergence in some simple situations. For recurrent models, online algorithms modify the parameterwhile the model is running, which further complicates the analysis withrespect to simple SGD.Local convergence for these various algorithms results from a single,more general set of assumptions, in the setup of learning dynamicalsystems online. Thus, these results can cover other variants ofthe algorithms considered.We adopt an ``ergodic'' rather than probabilistic viewpoint, working withempirical time averages instead of probability distributions. This ismore data-agnostic andcreates differences with respect to standard SGD theory,especially for the range of possible learning rates. For instance, withcycling or per-epoch reshuffling over a finite dataset instead of purei.i.d. sampling with replacement, empiricalaverages of gradients converge at rate $1/T$ insteadof $1/\sqrt{T}$ (cycling acts as a variance reduction method),theoretically allowingfor larger learning rates than in SGD.

Interpreting a Penalty as the Influence of a Bayesian Prior

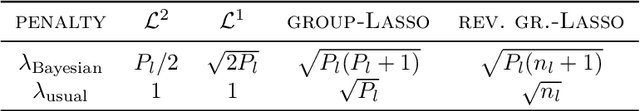
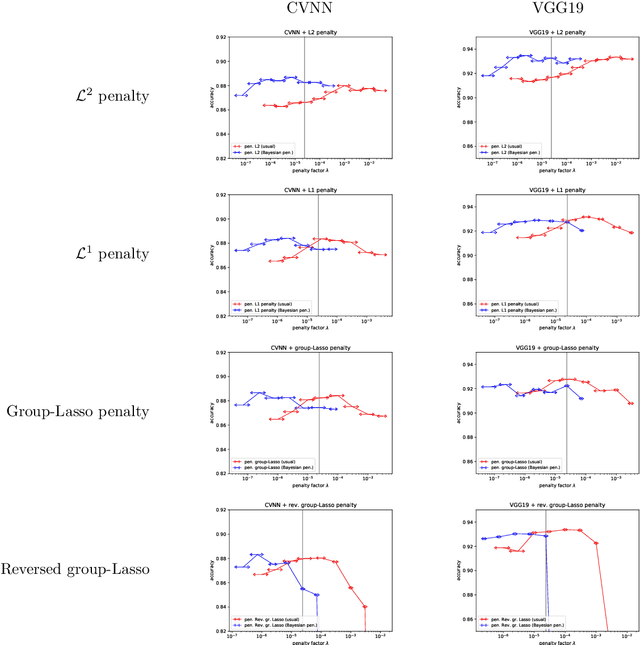
In machine learning, it is common to optimize the parameters of a probabilistic model, modulated by a somewhat ad hoc regularization term that penalizes some values of the parameters. Regularization terms appear naturally in Variational Inference (VI), a tractable way to approximate Bayesian posteriors: the loss to optimize contains a Kullback--Leibler divergence term between the approximate posterior and a Bayesian prior. We fully characterize which regularizers can arise this way, and provide a systematic way to compute the corresponding prior. This viewpoint also provides a prediction for useful values of the regularization factor in neural networks. We apply this framework to regularizers such as L1 or group-Lasso.

White-box vs Black-box: Bayes Optimal Strategies for Membership Inference

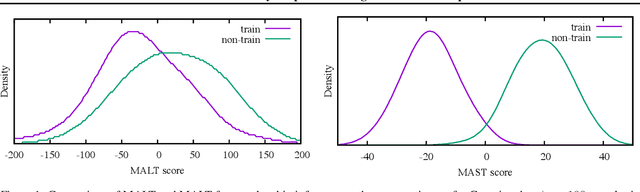
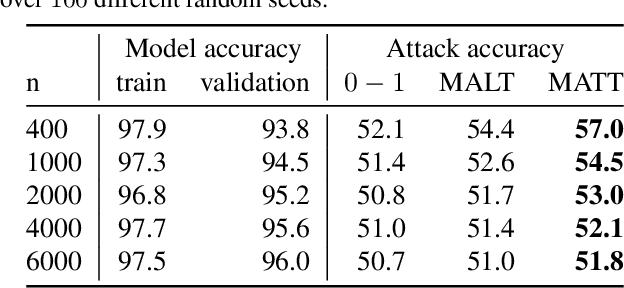
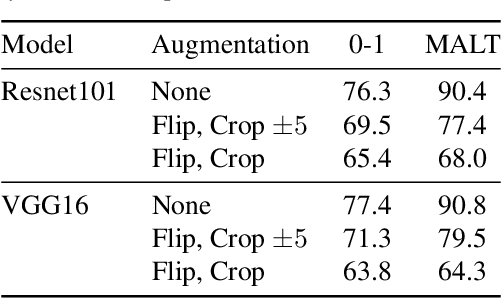
Membership inference determines, given a sample and trained parameters of a machine learning model, whether the sample was part of the training set. In this paper, we derive the optimal strategy for membership inference with a few assumptions on the distribution of the parameters. We show that optimal attacks only depend on the loss function, and thus black-box attacks are as good as white-box attacks. As the optimal strategy is not tractable, we provide approximations of it leading to several inference methods, and show that existing membership inference methods are coarser approximations of this optimal strategy. Our membership attacks outperform the state of the art in various settings, ranging from a simple logistic regression to more complex architectures and datasets, such as ResNet-101 and Imagenet.