Training of Physical Neural Networks

Physical neural networks (PNNs) are a class of neural-like networks that leverage the properties of physical systems to perform computation. While PNNs are so far a niche research area with small-scale laboratory demonstrations, they are arguably one of the most underappreciated important opportunities in modern AI. Could we train AI models 1000x larger than current ones? Could we do this and also have them perform inference locally and privately on edge devices, such as smartphones or sensors? Research over the past few years has shown that the answer to all these questions is likely "yes, with enough research": PNNs could one day radically change what is possible and practical for AI systems. To do this will however require rethinking both how AI models work, and how they are trained - primarily by considering the problems through the constraints of the underlying hardware physics. To train PNNs at large scale, many methods including backpropagation-based and backpropagation-free approaches are now being explored. These methods have various trade-offs, and so far no method has been shown to scale to the same scale and performance as the backpropagation algorithm widely used in deep learning today. However, this is rapidly changing, and a diverse ecosystem of training techniques provides clues for how PNNs may one day be utilized to create both more efficient realizations of current-scale AI models, and to enable unprecedented-scale models.

Quantum Equilibrium Propagation: Gradient-Descent Training of Quantum Systems

Equilibrium propagation (EP) is a training framework for energy-based systems, i.e. systems whose physics minimizes an energy function. EP has been explored in various classical physical systems such as resistor networks, elastic networks, the classical Ising model and coupled phase oscillators. A key advantage of EP is that it achieves gradient descent on a cost function using the physics of the system to extract the weight gradients, making it a candidate for the development of energy-efficient processors for machine learning. We extend EP to quantum systems, where the energy function that is minimized is the mean energy functional (expectation value of the Hamiltonian), whose minimum is the ground state of the Hamiltonian. As examples, we study the settings of the transverse-field Ising model and the quantum harmonic oscillator network -- quantum analogues of the Ising model and elastic network.

A Fast Algorithm to Simulate Nonlinear Resistive Networks

In the quest for energy-efficient artificial intelligence systems, resistor networks are attracting interest as an alternative to conventional GPU-based neural networks. These networks leverage the physics of electrical circuits for inference and can be optimized with local training techniques such as equilibrium propagation. Despite their potential advantage in terms of power consumption, the challenge of efficiently simulating these resistor networks has been a significant bottleneck to assess their scalability, with current methods either being limited to linear networks or relying on realistic, yet slow circuit simulators like SPICE. Assuming ideal circuit elements, we introduce a novel approach for the simulation of nonlinear resistive networks, which we frame as a quadratic programming problem with linear inequality constraints, and which we solve using a fast, exact coordinate descent algorithm. Our simulation methodology significantly outperforms existing SPICE-based simulations, enabling the training of networks up to 325 times larger at speeds 150 times faster, resulting in a 50,000-fold improvement in the ratio of network size to epoch duration. Our approach, adaptable to other electrical components, can foster more rapid progress in the simulations of nonlinear electrical networks.

Energy-based learning algorithms for analog computing: a comparative study

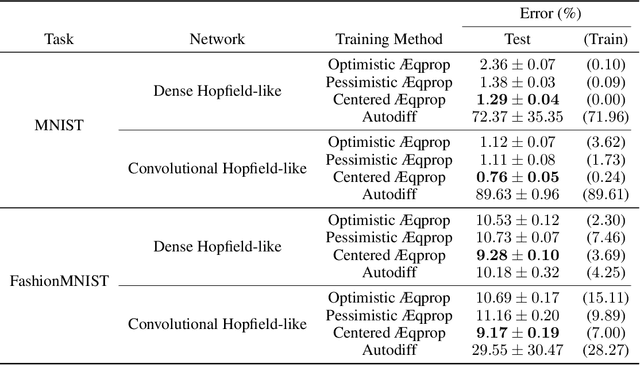
Energy-based learning algorithms have recently gained a surge of interest due to their compatibility with analog (post-digital) hardware. Existing algorithms include contrastive learning (CL), equilibrium propagation (EP) and coupled learning (CpL), all consisting in contrasting two states, and differing in the type of perturbation used to obtain the second state from the first one. However, these algorithms have never been explicitly compared on equal footing with same models and datasets, making it difficult to assess their scalability and decide which one to select in practice. In this work, we carry out a comparison of seven learning algorithms, namely CL and different variants of EP and CpL depending on the signs of the perturbations. Specifically, using these learning algorithms, we train deep convolutional Hopfield networks (DCHNs) on five vision tasks (MNIST, F-MNIST, SVHN, CIFAR-10 and CIFAR-100). We find that, while all algorithms yield comparable performance on MNIST, important differences in performance arise as the difficulty of the task increases. Our key findings reveal that negative perturbations are better than positive ones, and highlight the centered variant of EP (which uses two perturbations of opposite sign) as the best-performing algorithm. We also endorse these findings with theoretical arguments. Additionally, we establish new SOTA results with DCHNs on all five datasets, both in performance and speed. In particular, our DCHN simulations are 13.5 times faster with respect to Laborieux et al. (2021), which we achieve thanks to the use of a novel energy minimisation algorithm based on asynchronous updates, combined with reduced precision (16 bits).

A universal approximation theorem for nonlinear resistive networks

Resistor networks have recently had a surge of interest as substrates for energy-efficient self-learning machines. This work studies the computational capabilities of these resistor networks. We show that electrical networks composed of voltage sources, linear resistors, diodes and voltage-controlled voltage sources (VCVS) can implement any continuous functions. To prove it, we assume that the circuit elements are ideal and that the conductances of variable resistors and the amplification factors of the VCVS's can take arbitrary values -- arbitrarily small or arbitrarily large. The constructive nature of our proof could also inform the design of such self-learning electrical networks.

Agnostic Physics-Driven Deep Learning

This work establishes that a physical system can perform statistical learning without gradient computations, via an Agnostic Equilibrium Propagation (Aeqprop) procedure that combines energy minimization, homeostatic control, and nudging towards the correct response. In Aeqprop, the specifics of the system do not have to be known: the procedure is based only on external manipulations, and produces a stochastic gradient descent without explicit gradient computations. Thanks to nudging, the system performs a true, order-one gradient step for each training sample, in contrast with order-zero methods like reinforcement or evolutionary strategies, which rely on trial and error. This procedure considerably widens the range of potential hardware for statistical learning to any system with enough controllable parameters, even if the details of the system are poorly known. Aeqprop also establishes that in natural (bio)physical systems, genuine gradient-based statistical learning may result from generic, relatively simple mechanisms, without backpropagation and its requirement for analytic knowledge of partial derivatives.

A deep learning theory for neural networks grounded in physics

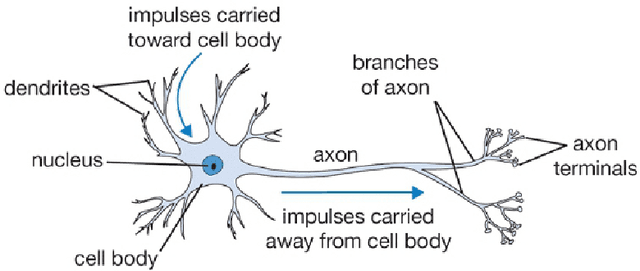
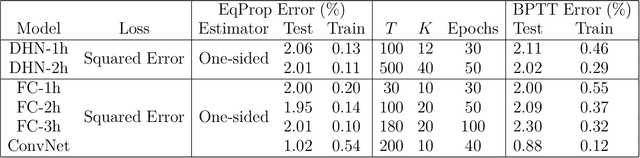
In the last decade, deep learning has become a major component of artificial intelligence, leading to a series of breakthroughs across a wide variety of domains. The workhorse of deep learning is the optimization of loss functions by stochastic gradient descent (SGD). Traditionally in deep learning, neural networks are differentiable mathematical functions, and the loss gradients required for SGD are computed with the backpropagation algorithm. However, the computer architectures on which these neural networks are implemented and trained suffer from speed and energy inefficiency issues, due to the separation of memory and processing in these architectures. To solve these problems, the field of neuromorphic computing aims at implementing neural networks on hardware architectures that merge memory and processing, just like brains do. In this thesis, we argue that building large, fast and efficient neural networks on neuromorphic architectures requires rethinking the algorithms to implement and train them. To this purpose, we present an alternative mathematical framework, also compatible with SGD, which offers the possibility to design neural networks in substrates that directly exploit the laws of physics. Our framework applies to a very broad class of models, namely systems whose state or dynamics are described by variational equations. The procedure to compute the loss gradients in such systems -- which in many practical situations requires solely locally available information for each trainable parameter -- is called equilibrium propagation (EqProp). Since many systems in physics and engineering can be described by variational principles, our framework has the potential to be applied to a broad variety of physical systems, whose applications extend to various fields of engineering, beyond neuromorphic computing.

Scaling Equilibrium Propagation to Deep ConvNets by Drastically Reducing its Gradient Estimator Bias

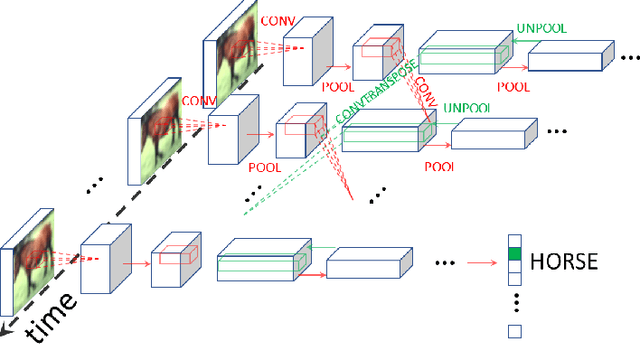
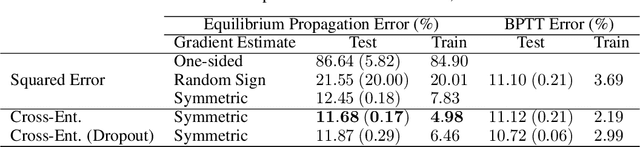
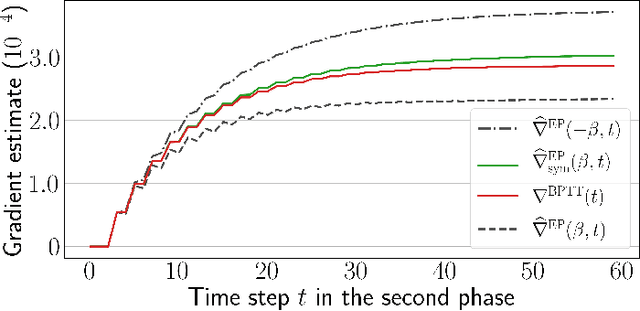
Equilibrium Propagation (EP) is a biologically-inspired counterpart of Backpropagation Through Time (BPTT) which, owing to its strong theoretical guarantees and the locality in space of its learning rule, fosters the design of energy-efficient hardware dedicated to learning. In practice, however, EP does not scale to visual tasks harder than MNIST. In this work, we show that a bias in the gradient estimate of EP, inherent in the use of finite nudging, is responsible for this phenomenon and that cancelling it allows training deep ConvNets by EP, including architectures with distinct forward and backward connections. These results highlight EP as a scalable approach to compute error gradients in deep neural networks, thereby motivating its hardware implementation.

Training End-to-End Analog Neural Networks with Equilibrium Propagation

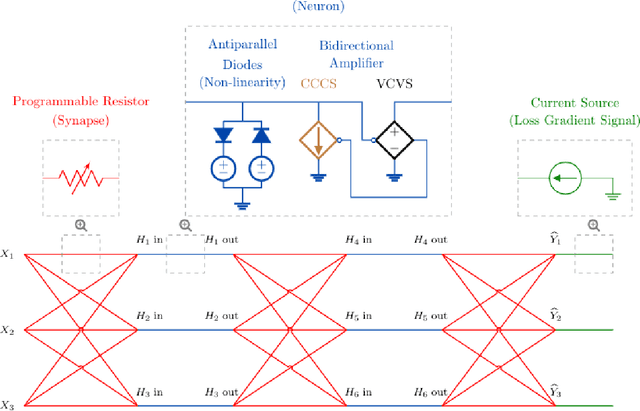
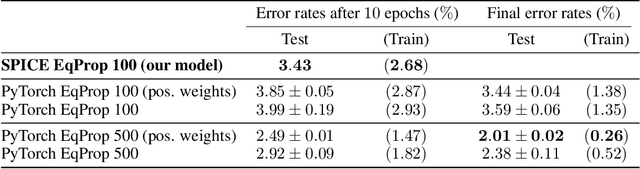
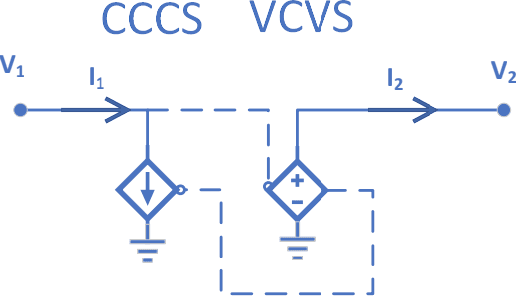
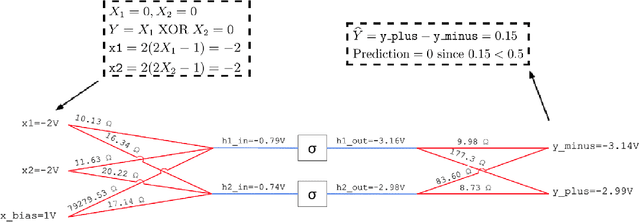
We introduce a principled method to train end-to-end analog neural networks by stochastic gradient descent. In these analog neural networks, the weights to be adjusted are implemented by the conductances of programmable resistive devices such as memristors [Chua, 1971], and the nonlinear transfer functions (or `activation functions') are implemented by nonlinear components such as diodes. We show mathematically that a class of analog neural networks (called nonlinear resistive networks) are energy-based models: they possess an energy function as a consequence of Kirchhoff's laws governing electrical circuits. This property enables us to train them using the Equilibrium Propagation framework [Scellier and Bengio, 2017]. Our update rule for each conductance, which is local and relies solely on the voltage drop across the corresponding resistor, is shown to compute the gradient of the loss function. Our numerical simulations, which use the SPICE-based Spectre simulation framework to simulate the dynamics of electrical circuits, demonstrate training on the MNIST classification task, performing comparably or better than equivalent-size software-based neural networks. Our work can guide the development of a new generation of ultra-fast, compact and low-power neural networks supporting on-chip learning.

Equilibrium Propagation with Continual Weight Updates

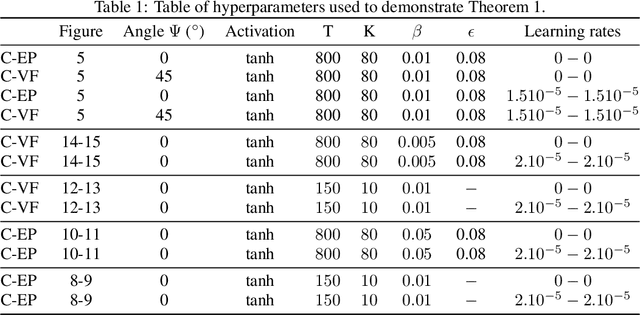
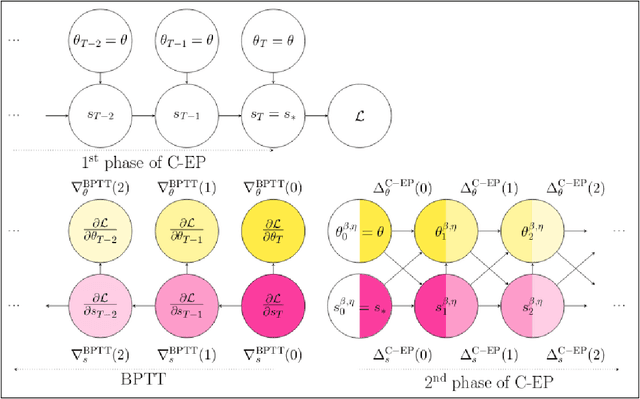
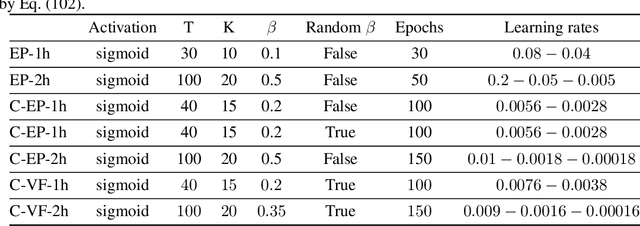
Equilibrium Propagation (EP) is a learning algorithm that bridges Machine Learning and Neuroscience, by computing gradients closely matching those of Backpropagation Through Time (BPTT), but with a learning rule local in space. Given an input $x$ and associated target $y$, EP proceeds in two phases: in the first phase neurons evolve freely towards a first steady state; in the second phase output neurons are nudged towards $y$ until they reach a second steady state. However, in existing implementations of EP, the learning rule is not local in time: the weight update is performed after the dynamics of the second phase have converged and requires information of the first phase that is no longer available physically. In this work, we propose a version of EP named Continual Equilibrium Propagation (C-EP) where neuron and synapse dynamics occur simultaneously throughout the second phase, so that the weight update becomes local in time. Such a learning rule local both in space and time opens the possibility of an extremely energy efficient hardware implementation of EP. We prove theoretically that, provided the learning rates are sufficiently small, at each time step of the second phase the dynamics of neurons and synapses follow the gradients of the loss given by BPTT (Theorem 1). We demonstrate training with C-EP on MNIST and generalize C-EP to neural networks where neurons are connected by asymmetric connections. We show through experiments that the more the network updates follows the gradients of BPTT, the best it performs in terms of training. These results bring EP a step closer to biology by better complying with hardware constraints while maintaining its intimate link with backpropagation.