Pierre-Yves Massé
CTU
Convergence of Online Adaptive and Recurrent Optimization Algorithms
May 12, 2020Abstract:We prove local convergence of several notable gradient descentalgorithms used inmachine learning, for which standard stochastic gradient descent theorydoes not apply. This includes, first, online algorithms for recurrent models and dynamicalsystems, such as \emph{Real-time recurrent learning} (RTRL) and its computationally lighter approximations NoBackTrack and UORO; second,several adaptive algorithms such as RMSProp, online natural gradient, and Adam with $\beta^2\to 1$.Despite local convergence being a relatively weak requirement for a newoptimization algorithm, no local analysis was available for these algorithms, as far aswe knew. Analysis of these algorithms does not immediately followfrom standard stochastic gradient (SGD) theory. In fact, Adam has been provedto lack local convergence in some simple situations. For recurrent models, online algorithms modify the parameterwhile the model is running, which further complicates the analysis withrespect to simple SGD.Local convergence for these various algorithms results from a single,more general set of assumptions, in the setup of learning dynamicalsystems online. Thus, these results can cover other variants ofthe algorithms considered.We adopt an ``ergodic'' rather than probabilistic viewpoint, working withempirical time averages instead of probability distributions. This ismore data-agnostic andcreates differences with respect to standard SGD theory,especially for the range of possible learning rates. For instance, withcycling or per-epoch reshuffling over a finite dataset instead of purei.i.d. sampling with replacement, empiricalaverages of gradients converge at rate $1/T$ insteadof $1/\sqrt{T}$ (cycling acts as a variance reduction method),theoretically allowingfor larger learning rates than in SGD.
Speed learning on the fly
Nov 08, 2015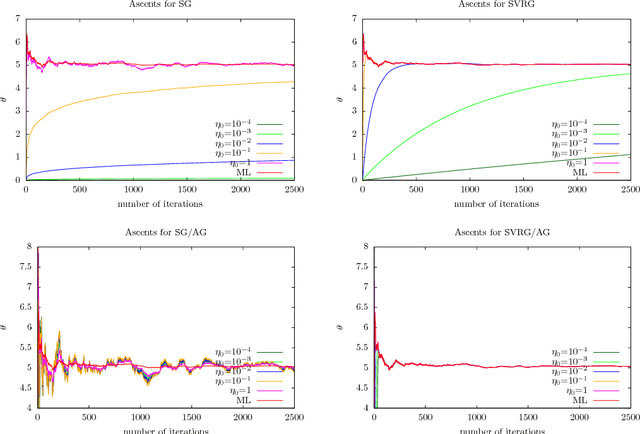
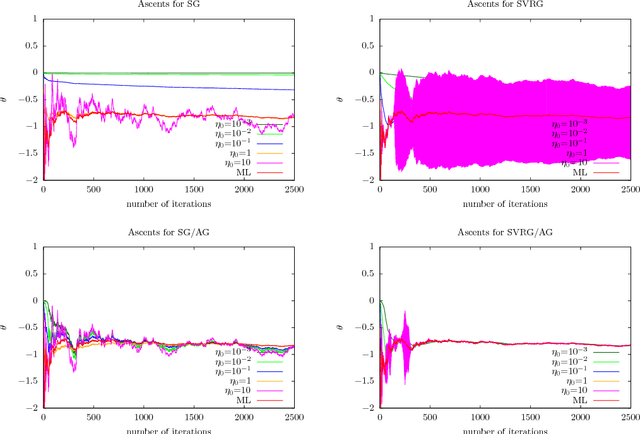
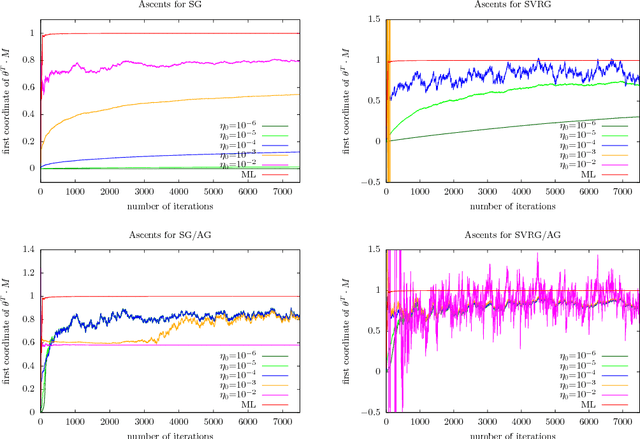
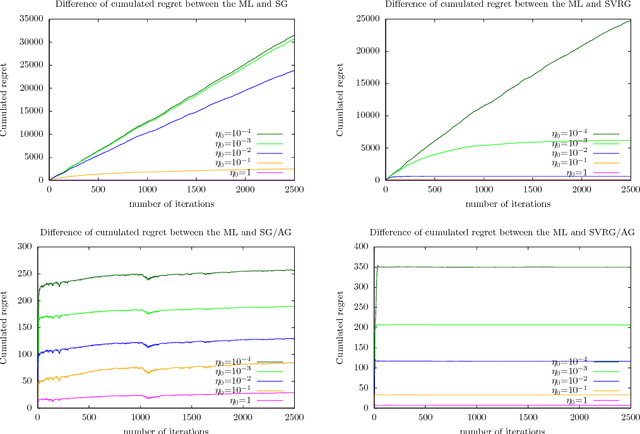
Abstract:The practical performance of online stochastic gradient descent algorithms is highly dependent on the chosen step size, which must be tediously hand-tuned in many applications. The same is true for more advanced variants of stochastic gradients, such as SAGA, SVRG, or AdaGrad. Here we propose to adapt the step size by performing a gradient descent on the step size itself, viewing the whole performance of the learning trajectory as a function of step size. Importantly, this adaptation can be computed online at little cost, without having to iterate backward passes over the full data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge