Likelihood-guided Regularization in Attention Based Models

The transformer architecture has demonstrated strong performance in classification tasks involving structured and high-dimensional data. However, its success often hinges on large- scale training data and careful regularization to prevent overfitting. In this paper, we intro- duce a novel likelihood-guided variational Ising-based regularization framework for Vision Transformers (ViTs), which simultaneously enhances model generalization and dynamically prunes redundant parameters. The proposed variational Ising-based regularization approach leverages Bayesian sparsification techniques to impose structured sparsity on model weights, allowing for adaptive architecture search during training. Unlike traditional dropout-based methods, which enforce fixed sparsity patterns, the variational Ising-based regularization method learns task-adaptive regularization, improving both efficiency and interpretability. We evaluate our approach on benchmark vision datasets, including MNIST, Fashion-MNIST, CIFAR-10, and CIFAR-100, demonstrating improved generalization under sparse, complex data and allowing for principled uncertainty quantification on both weights and selection parameters. Additionally, we show that the Ising regularizer leads to better-calibrated probability estimates and structured feature selection through uncertainty-aware attention mechanisms. Our results highlight the effectiveness of structured Bayesian sparsification in enhancing transformer-based architectures, offering a principled alternative to standard regularization techniques.

A Robust Asymmetric Kernel Function for Bayesian Optimization, with Application to Image Defect Detection in Manufacturing Systems

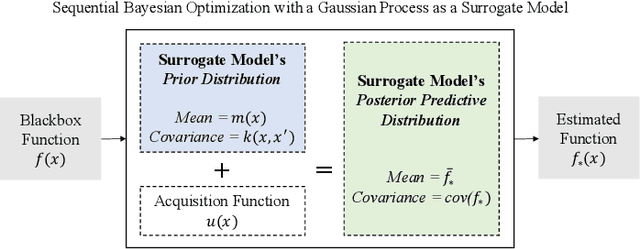
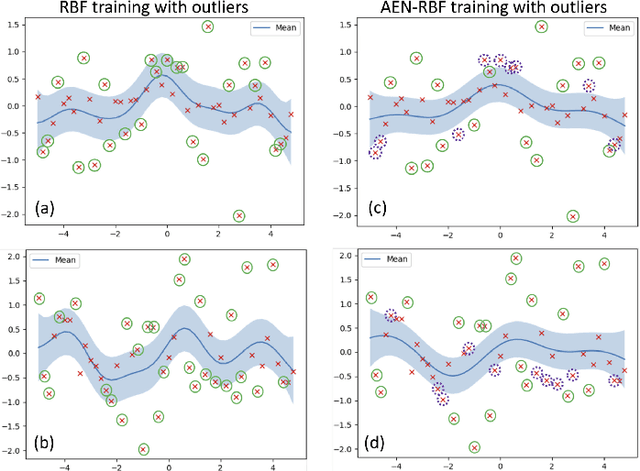
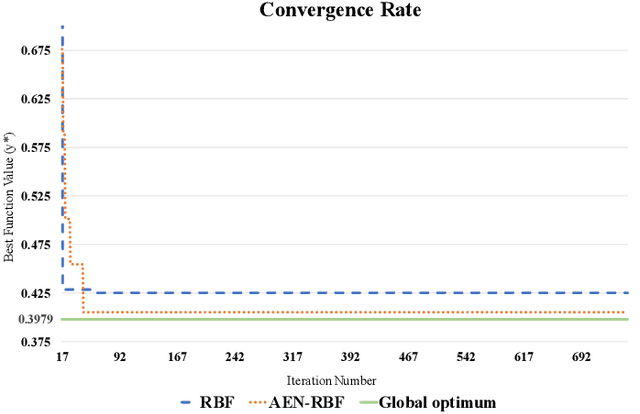
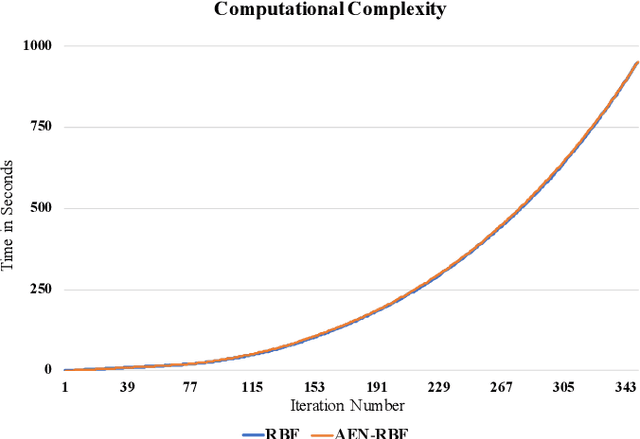
Some response surface functions in complex engineering systems are usually highly nonlinear, unformed, and expensive-to-evaluate. To tackle this challenge, Bayesian optimization, which conducts sequential design via a posterior distribution over the objective function, is a critical method used to find the global optimum of black-box functions. Kernel functions play an important role in shaping the posterior distribution of the estimated function. The widely used kernel function, e.g., radial basis function (RBF), is very vulnerable and susceptible to outliers; the existence of outliers is causing its Gaussian process surrogate model to be sporadic. In this paper, we propose a robust kernel function, Asymmetric Elastic Net Radial Basis Function (AEN-RBF). Its validity as a kernel function and computational complexity are evaluated. When compared to the baseline RBF kernel, we prove theoretically that AEN-RBF can realize smaller mean squared prediction error under mild conditions. The proposed AEN-RBF kernel function can also realize faster convergence to the global optimum. We also show that the AEN-RBF kernel function is less sensitive to outliers, and hence improves the robustness of the corresponding Bayesian optimization with Gaussian processes. Through extensive evaluations carried out on synthetic and real-world optimization problems, we show that AEN-RBF outperforms existing benchmark kernel functions.