Wotao Yin
Markov Chain Block Coordinate Descent
Nov 22, 2018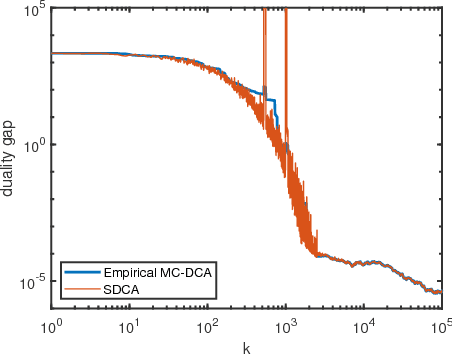
Abstract:The method of block coordinate gradient descent (BCD) has been a powerful method for large-scale optimization. This paper considers the BCD method that successively updates a series of blocks selected according to a Markov chain. This kind of block selection is neither i.i.d. random nor cyclic. On the other hand, it is a natural choice for some applications in distributed optimization and Markov decision process, where i.i.d. random and cyclic selections are either infeasible or very expensive. By applying mixing-time properties of a Markov chain, we prove convergence of Markov chain BCD for minimizing Lipschitz differentiable functions, which can be nonconvex. When the functions are convex and strongly convex, we establish both sublinear and linear convergence rates, respectively. We also present a method of Markov chain inertial BCD. Finally, we discuss potential applications.
Theoretical Linear Convergence of Unfolded ISTA and its Practical Weights and Thresholds
Nov 04, 2018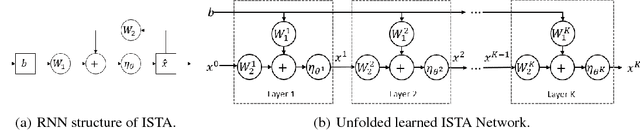
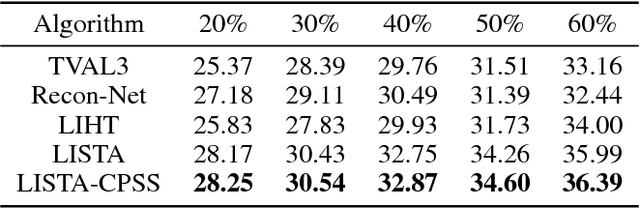

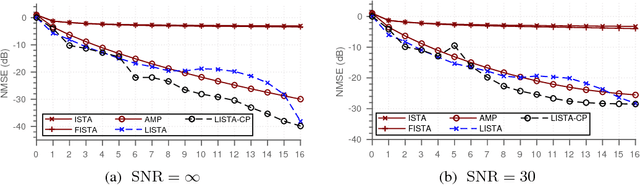
Abstract:In recent years, unfolding iterative algorithms as neural networks has become an empirical success in solving sparse recovery problems. However, its theoretical understanding is still immature, which prevents us from fully utilizing the power of neural networks. In this work, we study unfolded ISTA (Iterative Shrinkage Thresholding Algorithm) for sparse signal recovery. We introduce a weight structure that is necessary for asymptotic convergence to the true sparse signal. With this structure, unfolded ISTA can attain a linear convergence, which is better than the sublinear convergence of ISTA/FISTA in general cases. Furthermore, we propose to incorporate thresholding in the network to perform support selection, which is easy to implement and able to boost the convergence rate both theoretically and empirically. Extensive simulations, including sparse vector recovery and a compressive sensing experiment on real image data, corroborate our theoretical results and demonstrate their practical usefulness. We have made our codes publicly available: https://github.com/xchen-tamu/linear-lista-cpss.
On Markov Chain Gradient Descent
Sep 12, 2018
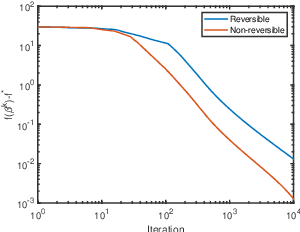
Abstract:Stochastic gradient methods are the workhorse (algorithms) of large-scale optimization problems in machine learning, signal processing, and other computational sciences and engineering. This paper studies Markov chain gradient descent, a variant of stochastic gradient descent where the random samples are taken on the trajectory of a Markov chain. Existing results of this method assume convex objectives and a reversible Markov chain and thus have their limitations. We establish new non-ergodic convergence under wider step sizes, for nonconvex problems, and for non-reversible finite-state Markov chains. Nonconvexity makes our method applicable to broader problem classes. Non-reversible finite-state Markov chains, on the other hand, can mix substatially faster. To obtain these results, we introduce a new technique that varies the mixing levels of the Markov chains. The reported numerical results validate our contributions.
Run-and-Inspect Method for Nonconvex Optimization and Global Optimality Bounds for R-Local Minimizers
Jun 29, 2018
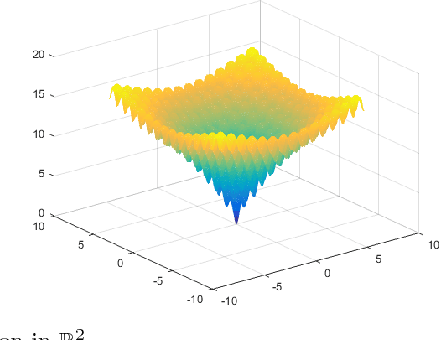
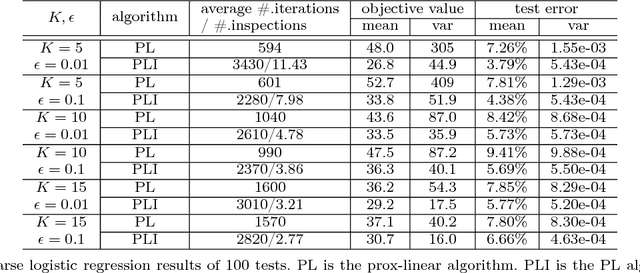
Abstract:Many optimization algorithms converge to stationary points. When the underlying problem is nonconvex, they may get trapped at local minimizers and occasionally stagnate near saddle points. We propose the Run-and-Inspect Method, which adds an "inspect" phase to existing algorithms that helps escape from non-global stationary points. The inspection samples a set of points in a radius $R$ around the current point. When a sample point yields a sufficient decrease in the objective, we move there and resume an existing algorithm. If no sufficient decrease is found, the current point is called an approximate $R$-local minimizer. We show that an $R$-local minimizer is globally optimal, up to a specific error depending on $R$, if the objective function can be implicitly decomposed into a smooth convex function plus a restricted function that is possibly nonconvex, nonsmooth. For high-dimensional problems, we introduce blockwise inspections to overcome the curse of dimensionality while still maintaining optimality bounds up to a factor equal to the number of blocks. Our method performs well on a set of artificial and realistic nonconvex problems by coupling with gradient descent, coordinate descent, EM, and prox-linear algorithms.
LAG: Lazily Aggregated Gradient for Communication-Efficient Distributed Learning
May 30, 2018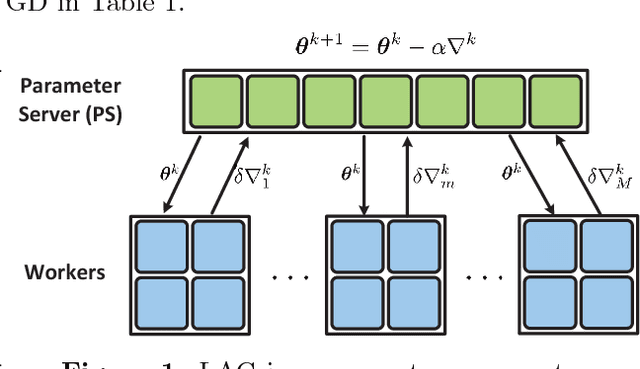


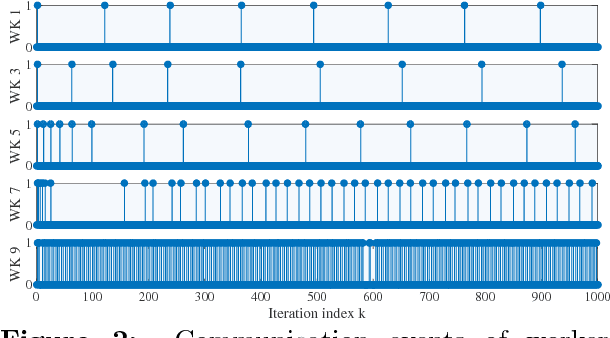
Abstract:This paper presents a new class of gradient methods for distributed machine learning that adaptively skip the gradient calculations to learn with reduced communication and computation. Simple rules are designed to detect slowly-varying gradients and, therefore, trigger the reuse of outdated gradients. The resultant gradient-based algorithms are termed Lazily Aggregated Gradient --- justifying our acronym LAG used henceforth. Theoretically, the merits of this contribution are: i) the convergence rate is the same as batch gradient descent in strongly-convex, convex, and nonconvex smooth cases; and, ii) if the distributed datasets are heterogeneous (quantified by certain measurable constants), the communication rounds needed to achieve a targeted accuracy are reduced thanks to the adaptive reuse of lagged gradients. Numerical experiments on both synthetic and real data corroborate a significant communication reduction compared to alternatives.
Redundancy Techniques for Straggler Mitigation in Distributed Optimization and Learning
Mar 14, 2018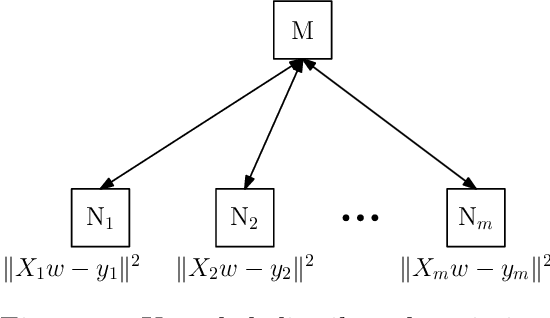

Abstract:Performance of distributed optimization and learning systems is bottlenecked by "straggler" nodes and slow communication links, which significantly delay computation. We propose a distributed optimization framework where the dataset is "encoded" to have an over-complete representation with built-in redundancy, and the straggling nodes in the system are dynamically left out of the computation at every iteration, whose loss is compensated by the embedded redundancy. We show that oblivious application of several popular optimization algorithms on encoded data, including gradient descent, L-BFGS, proximal gradient under data parallelism, and coordinate descent under model parallelism, converge to either approximate or exact solutions of the original problem when stragglers are treated as erasures. These convergence results are deterministic, i.e., they establish sample path convergence for arbitrary sequences of delay patterns or distributions on the nodes, and are independent of the tail behavior of the delay distribution. We demonstrate that equiangular tight frames have desirable properties as encoding matrices, and propose efficient mechanisms for encoding large-scale data. We implement the proposed technique on Amazon EC2 clusters, and demonstrate its performance over several learning problems, including matrix factorization, LASSO, ridge regression and logistic regression, and compare the proposed method with uncoded, asynchronous, and data replication strategies.
Straggler Mitigation in Distributed Optimization Through Data Encoding
Jan 22, 2018
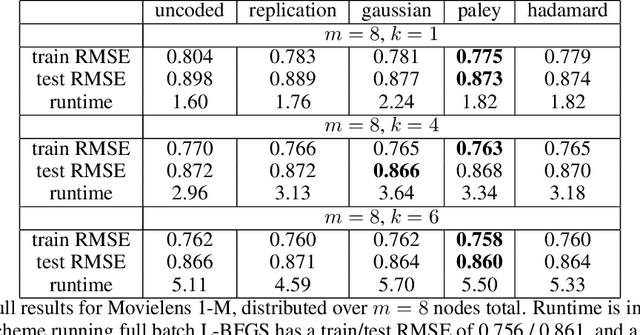
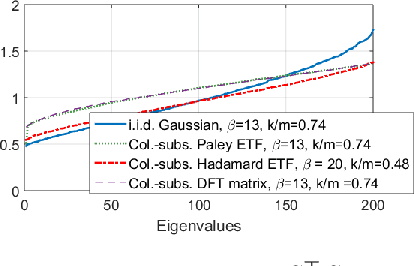
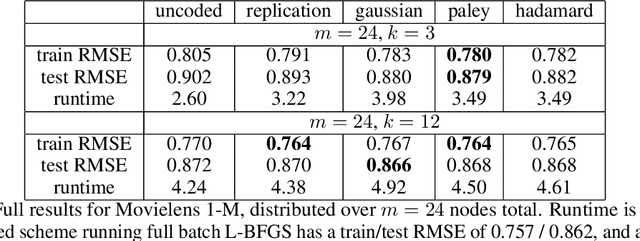
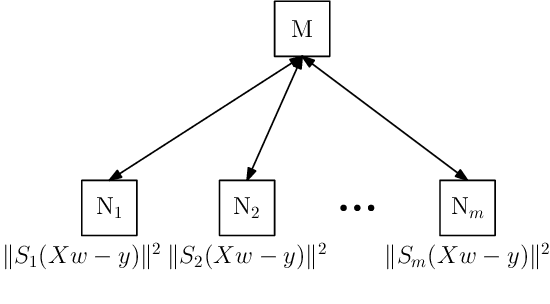
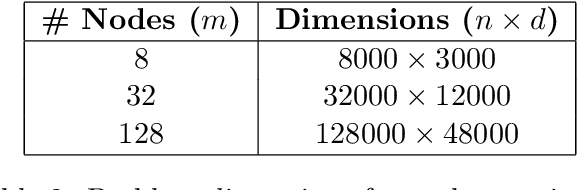
Abstract:Slow running or straggler tasks can significantly reduce computation speed in distributed computation. Recently, coding-theory-inspired approaches have been applied to mitigate the effect of straggling, through embedding redundancy in certain linear computational steps of the optimization algorithm, thus completing the computation without waiting for the stragglers. In this paper, we propose an alternate approach where we embed the redundancy directly in the data itself, and allow the computation to proceed completely oblivious to encoding. We propose several encoding schemes, and demonstrate that popular batch algorithms, such as gradient descent and L-BFGS, applied in a coding-oblivious manner, deterministically achieve sample path linear convergence to an approximate solution of the original problem, using an arbitrarily varying subset of the nodes at each iteration. Moreover, this approximation can be controlled by the amount of redundancy and the number of nodes used in each iteration. We provide experimental results demonstrating the advantage of the approach over uncoded and data replication strategies.
Denoising Prior Driven Deep Neural Network for Image Restoration
Jan 21, 2018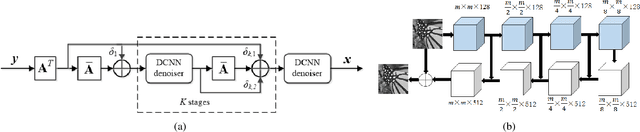



Abstract:Deep neural networks (DNNs) have shown very promising results for various image restoration (IR) tasks. However, the design of network architectures remains a major challenging for achieving further improvements. While most existing DNN-based methods solve the IR problems by directly mapping low quality images to desirable high-quality images, the observation models characterizing the image degradation processes have been largely ignored. In this paper, we first propose a denoising-based IR algorithm, whose iterative steps can be computed efficiently. Then, the iterative process is unfolded into a deep neural network, which is composed of multiple denoisers modules interleaved with back-projection (BP) modules that ensure the observation consistencies. A convolutional neural network (CNN) based denoiser that can exploit the multi-scale redundancies of natural images is proposed. As such, the proposed network not only exploits the powerful denoising ability of DNNs, but also leverages the prior of the observation model. Through end-to-end training, both the denoisers and the BP modules can be jointly optimized. Experimental results on several IR tasks, e.g., image denoising, super-resolution and deblurring show that the proposed method can lead to very competitive and often state-of-the-art results on several IR tasks, including image denoising, deblurring and super-resolution.
On the Convergence of Asynchronous Parallel Iteration with Unbounded Delays
Nov 15, 2017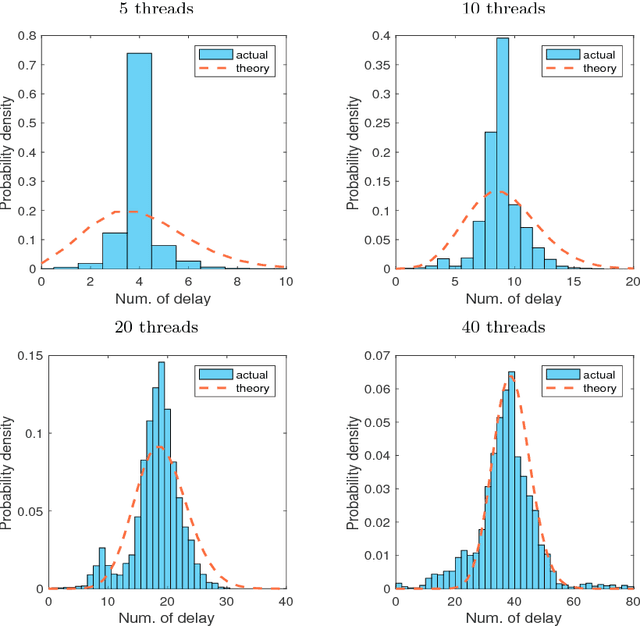
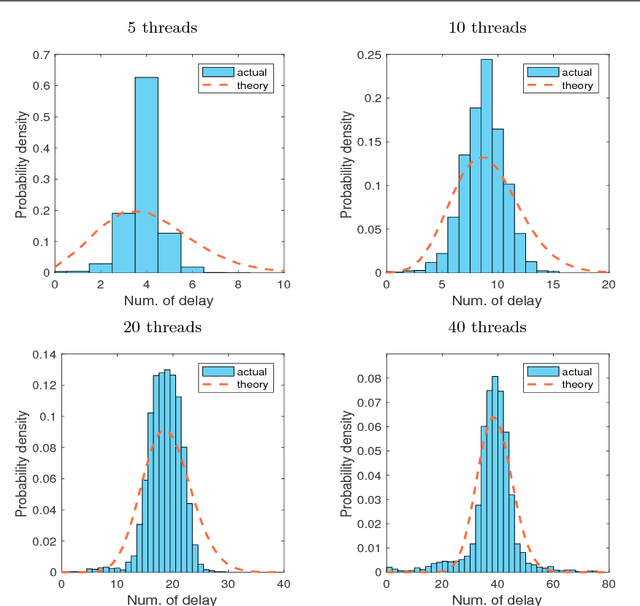
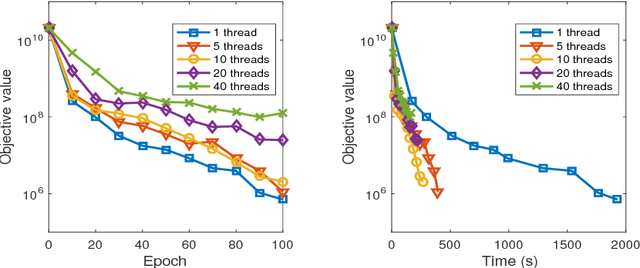
Abstract:Recent years have witnessed the surge of asynchronous parallel (async-parallel) iterative algorithms due to problems involving very large-scale data and a large number of decision variables. Because of asynchrony, the iterates are computed with outdated information, and the age of the outdated information, which we call delay, is the number of times it has been updated since its creation. Almost all recent works prove convergence under the assumption of a finite maximum delay and set their stepsize parameters accordingly. However, the maximum delay is practically unknown. This paper presents convergence analysis of an async-parallel method from a probabilistic viewpoint, and it allows for large unbounded delays. An explicit formula of stepsize that guarantees convergence is given depending on delays' statistics. With $p+1$ identical processors, we empirically measured that delays closely follow the Poisson distribution with parameter $p$, matching our theoretical model, and thus the stepsize can be set accordingly. Simulations on both convex and nonconvex optimization problems demonstrate the validness of our analysis and also show that the existing maximum-delay induced stepsize is too conservative, often slowing down the convergence of the algorithm.
Online Convolutional Dictionary Learning
Aug 30, 2017

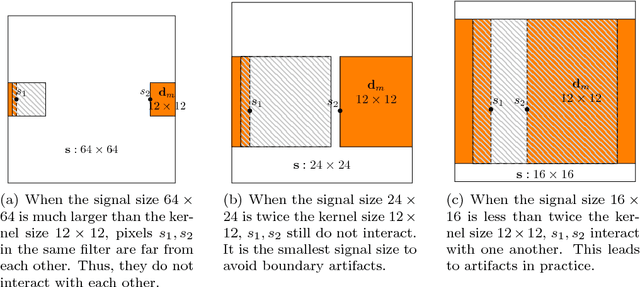
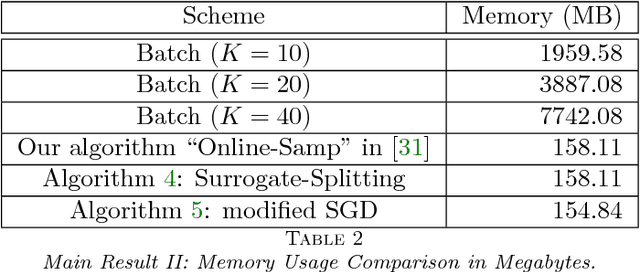
Abstract:While a number of different algorithms have recently been proposed for convolutional dictionary learning, this remains an expensive problem. The single biggest impediment to learning from large training sets is the memory requirements, which grow at least linearly with the size of the training set since all existing methods are batch algorithms. The work reported here addresses this limitation by extending online dictionary learning ideas to the convolutional context.
* Accepted to be presented at ICIP 2017
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge