Accurate and scalable exchange-correlation with deep learning

Density Functional Theory (DFT) is the most widely used electronic structure method for predicting the properties of molecules and materials. Although DFT is, in principle, an exact reformulation of the Schr\"odinger equation, practical applications rely on approximations to the unknown exchange-correlation (XC) functional. Most existing XC functionals are constructed using a limited set of increasingly complex, hand-crafted features that improve accuracy at the expense of computational efficiency. Yet, no current approximation achieves the accuracy and generality for predictive modeling of laboratory experiments at chemical accuracy -- typically defined as errors below 1 kcal/mol. In this work, we present Skala, a modern deep learning-based XC functional that bypasses expensive hand-designed features by learning representations directly from data. Skala achieves chemical accuracy for atomization energies of small molecules while retaining the computational efficiency typical of semi-local DFT. This performance is enabled by training on an unprecedented volume of high-accuracy reference data generated using computationally intensive wavefunction-based methods. Notably, Skala systematically improves with additional training data covering diverse chemistry. By incorporating a modest amount of additional high-accuracy data tailored to chemistry beyond atomization energies, Skala achieves accuracy competitive with the best-performing hybrid functionals across general main group chemistry, at the cost of semi-local DFT. As the training dataset continues to expand, Skala is poised to further enhance the predictive power of first-principles simulations.

Translation Equivariant Transformer Neural Processes

The effectiveness of neural processes (NPs) in modelling posterior prediction maps -- the mapping from data to posterior predictive distributions -- has significantly improved since their inception. This improvement can be attributed to two principal factors: (1) advancements in the architecture of permutation invariant set functions, which are intrinsic to all NPs; and (2) leveraging symmetries present in the true posterior predictive map, which are problem dependent. Transformers are a notable development in permutation invariant set functions, and their utility within NPs has been demonstrated through the family of models we refer to as TNPs. Despite significant interest in TNPs, little attention has been given to incorporating symmetries. Notably, the posterior prediction maps for data that are stationary -- a common assumption in spatio-temporal modelling -- exhibit translation equivariance. In this paper, we introduce of a new family of translation equivariant TNPs that incorporate translation equivariance. Through an extensive range of experiments on synthetic and real-world spatio-temporal data, we demonstrate the effectiveness of TE-TNPs relative to their non-translation-equivariant counterparts and other NP baselines.

Noise-Aware Differentially Private Regression via Meta-Learning

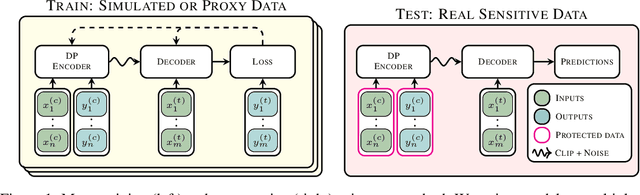
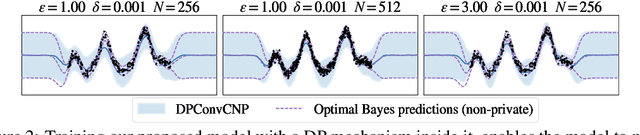
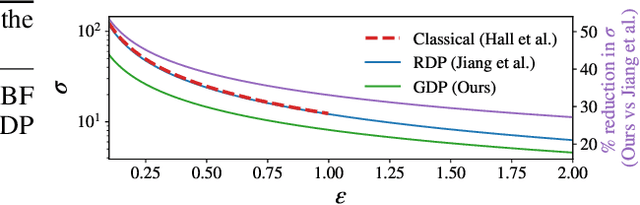
Many high-stakes applications require machine learning models that protect user privacy and provide well-calibrated, accurate predictions. While Differential Privacy (DP) is the gold standard for protecting user privacy, standard DP mechanisms typically significantly impair performance. One approach to mitigating this issue is pre-training models on simulated data before DP learning on the private data. In this work we go a step further, using simulated data to train a meta-learning model that combines the Convolutional Conditional Neural Process (ConvCNP) with an improved functional DP mechanism of Hall et al. [2013] yielding the DPConvCNP. DPConvCNP learns from simulated data how to map private data to a DP predictive model in one forward pass, and then provides accurate, well-calibrated predictions. We compare DPConvCNP with a DP Gaussian Process (GP) baseline with carefully tuned hyperparameters. The DPConvCNP outperforms the GP baseline, especially on non-Gaussian data, yet is much faster at test time and requires less tuning.

Aurora: A Foundation Model of the Atmosphere

Deep learning foundation models are revolutionizing many facets of science by leveraging vast amounts of data to learn general-purpose representations that can be adapted to tackle diverse downstream tasks. Foundation models hold the promise to also transform our ability to model our planet and its subsystems by exploiting the vast expanse of Earth system data. Here we introduce Aurora, a large-scale foundation model of the atmosphere trained on over a million hours of diverse weather and climate data. Aurora leverages the strengths of the foundation modelling approach to produce operational forecasts for a wide variety of atmospheric prediction problems, including those with limited training data, heterogeneous variables, and extreme events. In under a minute, Aurora produces 5-day global air pollution predictions and 10-day high-resolution weather forecasts that outperform state-of-the-art classical simulation tools and the best specialized deep learning models. Taken together, these results indicate that foundation models can transform environmental forecasting.

Aardvark Weather: end-to-end data-driven weather forecasting

Machine learning is revolutionising medium-range weather prediction. However it has only been applied to specific and individual components of the weather prediction pipeline. Consequently these data-driven approaches are unable to be deployed without input from conventional operational numerical weather prediction (NWP) systems, which is computationally costly and does not support end-to-end optimisation. In this work, we take a radically different approach and replace the entire NWP pipeline with a machine learning model. We present Aardvark Weather, the first end-to-end data-driven forecasting system which takes raw observations as input and provides both global and local forecasts. These global forecasts are produced for 24 variables at multiple pressure levels at one-degree spatial resolution and 24 hour temporal resolution, and are skillful with respect to hourly climatology at five to seven day lead times. Local forecasts are produced for temperature, mean sea level pressure, and wind speed at a geographically diverse set of weather stations, and are skillful with respect to an IFS-HRES interpolation baseline at multiple lead-times. Aardvark, by virtue of its simplicity and scalability, opens the door to a new paradigm for performing accurate and efficient data-driven medium-range weather forecasting.

Autoregressive Conditional Neural Processes

Conditional neural processes (CNPs; Garnelo et al., 2018a) are attractive meta-learning models which produce well-calibrated predictions and are trainable via a simple maximum likelihood procedure. Although CNPs have many advantages, they are unable to model dependencies in their predictions. Various works propose solutions to this, but these come at the cost of either requiring approximate inference or being limited to Gaussian predictions. In this work, we instead propose to change how CNPs are deployed at test time, without any modifications to the model or training procedure. Instead of making predictions independently for every target point, we autoregressively define a joint predictive distribution using the chain rule of probability, taking inspiration from the neural autoregressive density estimator (NADE) literature. We show that this simple procedure allows factorised Gaussian CNPs to model highly dependent, non-Gaussian predictive distributions. Perhaps surprisingly, in an extensive range of tasks with synthetic and real data, we show that CNPs in autoregressive (AR) mode not only significantly outperform non-AR CNPs, but are also competitive with more sophisticated models that are significantly more computationally expensive and challenging to train. This performance is remarkable given that AR CNPs are not trained to model joint dependencies. Our work provides an example of how ideas from neural distribution estimation can benefit neural processes, and motivates research into the AR deployment of other neural process models.

Active Learning with Convolutional Gaussian Neural Processes for Environmental Sensor Placement

Deploying environmental measurement stations can be a costly and time-consuming procedure, especially in remote regions that are difficult to access, such as Antarctica. Therefore, it is crucial that sensors are placed as efficiently as possible, maximising the informativeness of their measurements. This can be tackled by fitting a probabilistic model to existing data and identifying placements that would maximally reduce the model's uncertainty. The models most widely used for this purpose are Gaussian processes (GPs). However, designing a GP covariance which captures the complex behaviour of non-stationary spatiotemporal data is a difficult task. Further, the computational cost of GPs makes them challenging to scale to large environmental datasets. In this work, we explore using a convolutional Gaussian neural process (ConvGNP) to address these issues. A ConvGNP is a meta-learning model that uses neural networks to parameterise a GP predictive. Our model is data-driven, flexible, efficient, and permits multiple input predictors of gridded or scattered modalities. Using simulated surface air temperature fields over Antarctica as ground truth, we show that a ConvGNP significantly outperforms a non-stationary GP baseline in terms of predictive performance. We then use the ConvGNP in an Antarctic sensor placement toy experiment, yielding promising results.

Sparse Gaussian Process Hyperparameters: Optimize or Integrate?

The kernel function and its hyperparameters are the central model selection choice in a Gaussian proces (Rasmussen and Williams, 2006). Typically, the hyperparameters of the kernel are chosen by maximising the marginal likelihood, an approach known as Type-II maximum likelihood (ML-II). However, ML-II does not account for hyperparameter uncertainty, and it is well-known that this can lead to severely biased estimates and an underestimation of predictive uncertainty. While there are several works which employ a fully Bayesian characterisation of GPs, relatively few propose such approaches for the sparse GPs paradigm. In this work we propose an algorithm for sparse Gaussian process regression which leverages MCMC to sample from the hyperparameter posterior within the variational inducing point framework of Titsias (2009). This work is closely related to Hensman et al. (2015b) but side-steps the need to sample the inducing points, thereby significantly improving sampling efficiency in the Gaussian likelihood case. We compare this scheme against natural baselines in literature along with stochastic variational GPs (SVGPs) along with an extensive computational analysis.

A Note on the Chernoff Bound for Random Variables in the Unit Interval

The Chernoff bound is a well-known tool for obtaining a high probability bound on the expectation of a Bernoulli random variable in terms of its sample average. This bound is commonly used in statistical learning theory to upper bound the generalisation risk of a hypothesis in terms of its empirical risk on held-out data, for the case of a binary-valued loss function. However, the extension of this bound to the case of random variables taking values in the unit interval is less well known in the community. In this note we provide a proof of this extension for convenience and future reference.

Practical Conditional Neural Processes Via Tractable Dependent Predictions

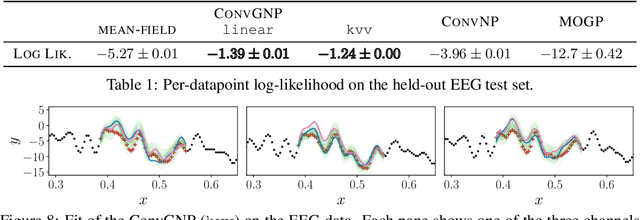
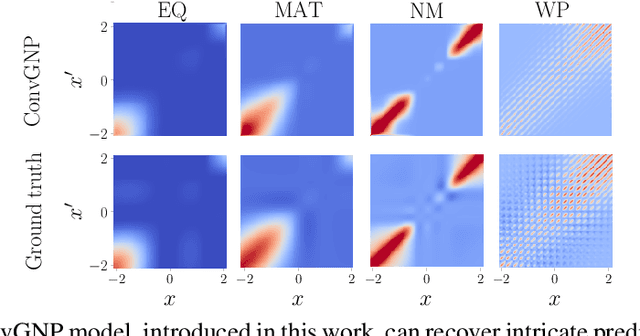
Conditional Neural Processes (CNPs; Garnelo et al., 2018a) are meta-learning models which leverage the flexibility of deep learning to produce well-calibrated predictions and naturally handle off-the-grid and missing data. CNPs scale to large datasets and train with ease. Due to these features, CNPs appear well-suited to tasks from environmental sciences or healthcare. Unfortunately, CNPs do not produce correlated predictions, making them fundamentally inappropriate for many estimation and decision making tasks. Predicting heat waves or floods, for example, requires modelling dependencies in temperature or precipitation over time and space. Existing approaches which model output dependencies, such as Neural Processes (NPs; Garnelo et al., 2018b) or the FullConvGNP (Bruinsma et al., 2021), are either complicated to train or prohibitively expensive. What is needed is an approach which provides dependent predictions, but is simple to train and computationally tractable. In this work, we present a new class of Neural Process models that make correlated predictions and support exact maximum likelihood training that is simple and scalable. We extend the proposed models by using invertible output transformations, to capture non-Gaussian output distributions. Our models can be used in downstream estimation tasks which require dependent function samples. By accounting for output dependencies, our models show improved predictive performance on a range of experiments with synthetic and real data.