Aardvark Weather: end-to-end data-driven weather forecasting

Machine learning is revolutionising medium-range weather prediction. However it has only been applied to specific and individual components of the weather prediction pipeline. Consequently these data-driven approaches are unable to be deployed without input from conventional operational numerical weather prediction (NWP) systems, which is computationally costly and does not support end-to-end optimisation. In this work, we take a radically different approach and replace the entire NWP pipeline with a machine learning model. We present Aardvark Weather, the first end-to-end data-driven forecasting system which takes raw observations as input and provides both global and local forecasts. These global forecasts are produced for 24 variables at multiple pressure levels at one-degree spatial resolution and 24 hour temporal resolution, and are skillful with respect to hourly climatology at five to seven day lead times. Local forecasts are produced for temperature, mean sea level pressure, and wind speed at a geographically diverse set of weather stations, and are skillful with respect to an IFS-HRES interpolation baseline at multiple lead-times. Aardvark, by virtue of its simplicity and scalability, opens the door to a new paradigm for performing accurate and efficient data-driven medium-range weather forecasting.

Ice Core Dating using Probabilistic Programming

Ice cores record crucial information about past climate. However, before ice core data can have scientific value, the chronology must be inferred by estimating the age as a function of depth. Under certain conditions, chemicals locked in the ice display quasi-periodic cycles that delineate annual layers. Manually counting these noisy seasonal patterns to infer the chronology can be an imperfect and time-consuming process, and does not capture uncertainty in a principled fashion. In addition, several ice cores may be collected from a region, introducing an aspect of spatial correlation between them. We present an exploration of the use of probabilistic models for automatic dating of ice cores, using probabilistic programming to showcase its use for prototyping, automatic inference and maintainability, and demonstrate common failure modes of these tools.

Combining Pseudo-Point and State Space Approximations for Sum-Separable Gaussian Processes

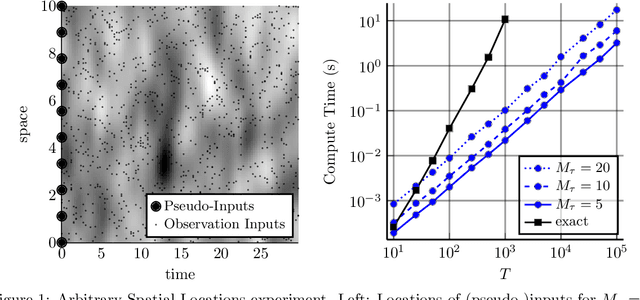
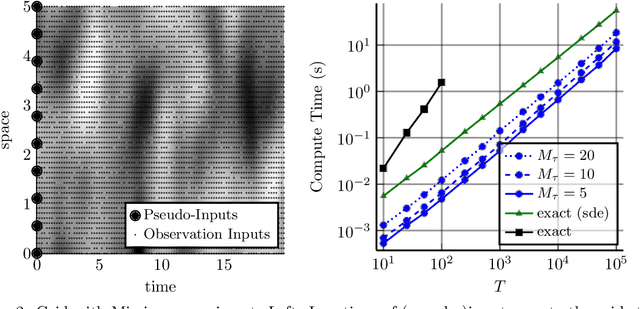
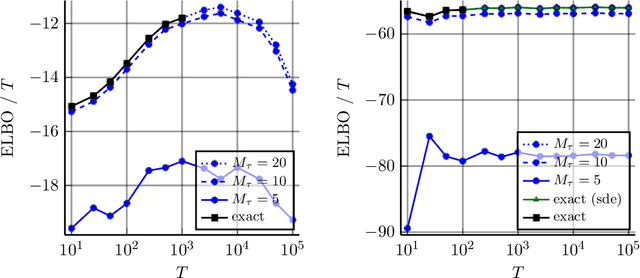
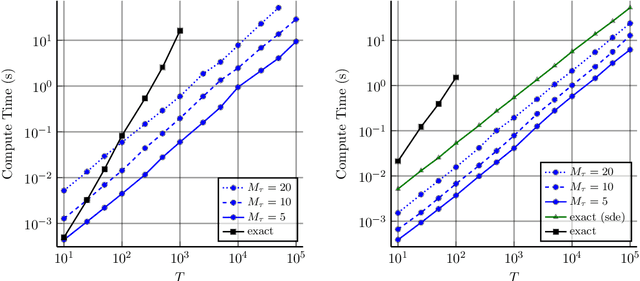
Gaussian processes (GPs) are important probabilistic tools for inference and learning in spatio-temporal modelling problems such as those in climate science and epidemiology. However, existing GP approximations do not simultaneously support large numbers of off-the-grid spatial data-points and long time-series which is a hallmark of many applications. Pseudo-point approximations, one of the gold-standard methods for scaling GPs to large data sets, are well suited for handling off-the-grid spatial data. However, they cannot handle long temporal observation horizons effectively reverting to cubic computational scaling in the time dimension. State space GP approximations are well suited to handling temporal data, if the temporal GP prior admits a Markov form, leading to linear complexity in the number of temporal observations, but have a cubic spatial cost and cannot handle off-the-grid spatial data. In this work we show that there is a simple and elegant way to combine pseudo-point methods with the state space GP approximation framework to get the best of both worlds. The approach hinges on a surprising conditional independence property which applies to space--time separable GPs. We demonstrate empirically that the combined approach is more scalable and applicable to a greater range of spatio-temporal problems than either method on its own.

Convolutional conditional neural processes for local climate downscaling

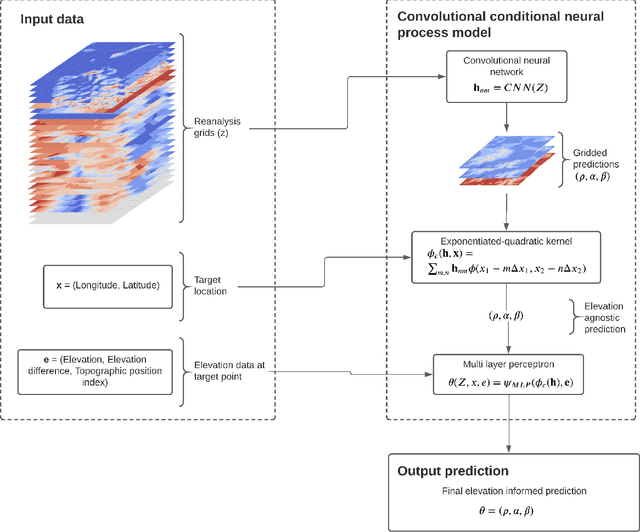
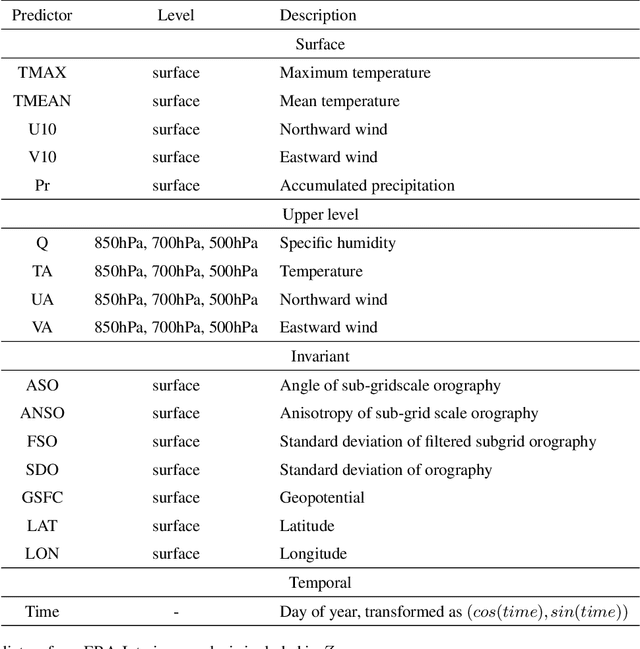
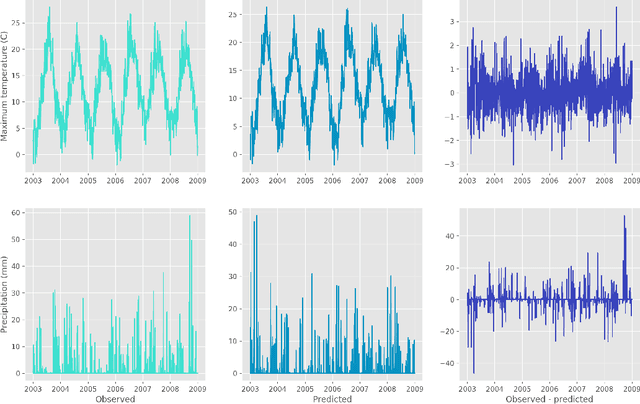
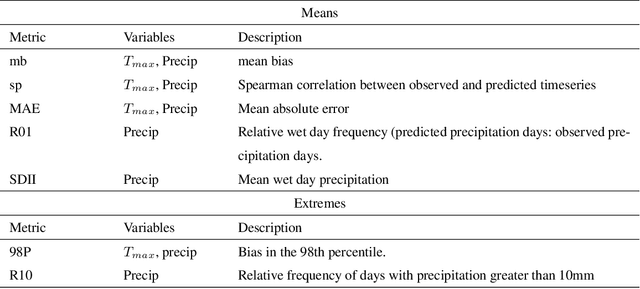
A new model is presented for multisite statistical downscaling of temperature and precipitation using convolutional conditional neural processes (convCNPs). ConvCNPs are a recently developed class of models that allow deep learning techniques to be applied to off-the-grid spatio-temporal data. This model has a substantial advantage over existing downscaling methods in that the trained model can be used to generate multisite predictions at an arbitrary set of locations, regardless of the availability of training data. The convCNP model is shown to outperform an ensemble of existing downscaling techniques over Europe for both temperature and precipitation taken from the VALUE intercomparison project. The model also outperforms an approach that uses Gaussian processes to interpolate single-site downscaling models at unseen locations. Importantly, substantial improvement is seen in the representation of extreme precipitation events. These results indicate that the convCNP is a robust downscaling model suitable for generating localised projections for use in climate impact studies, and motivates further research into applications of deep learning techniques in statistical downscaling.

Sparse Gaussian Process Variational Autoencoders

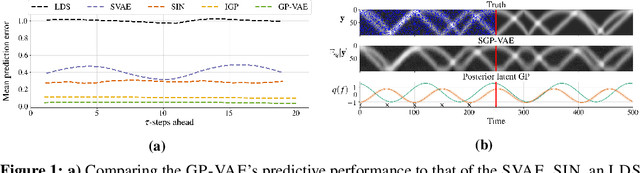
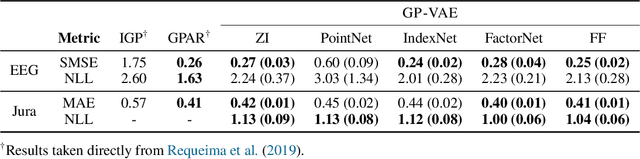
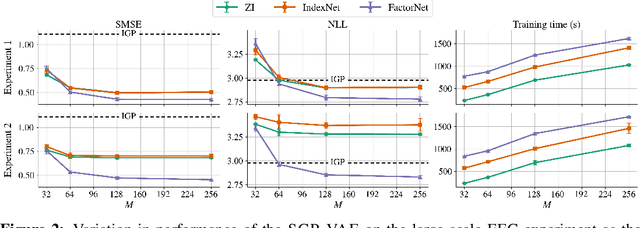
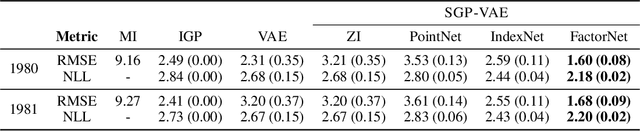
Large, multi-dimensional spatio-temporal datasets are omnipresent in modern science and engineering. An effective framework for handling such data are Gaussian process deep generative models (GP-DGMs), which employ GP priors over the latent variables of DGMs. Existing approaches for performing inference in GP-DGMs do not support sparse GP approximations based on inducing points, which are essential for the computational efficiency of GPs, nor do they handle missing data -- a natural occurrence in many spatio-temporal datasets -- in a principled manner. We address these shortcomings with the development of the sparse Gaussian process variational autoencoder (SGP-VAE), characterised by the use of partial inference networks for parameterising sparse GP approximations. Leveraging the benefits of amortised variational inference, the SGP-VAE enables inference in multi-output sparse GPs on previously unobserved data with no additional training. The SGP-VAE is evaluated in a variety of experiments where it outperforms alternative approaches including multi-output GPs and structured VAEs.

Scalable Exact Inference in Multi-Output Gaussian Processes

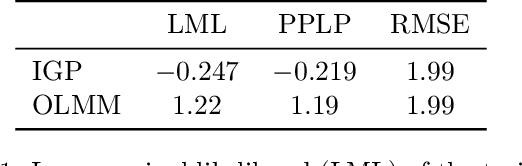
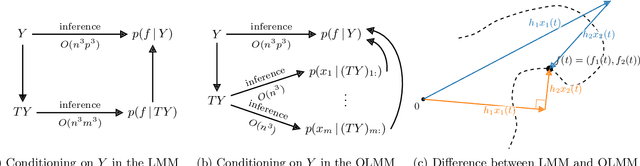
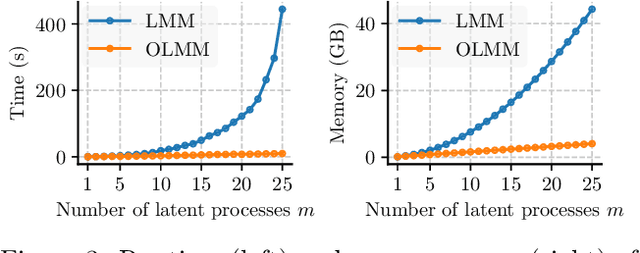
Multi-output Gaussian processes (MOGPs) leverage the flexibility and interpretability of GPs while capturing structure across outputs, which is desirable, for example, in spatio-temporal modelling. The key problem with MOGPs is the cubic computational scaling in the number of both inputs (e.g., time points or locations), n, and outputs, p. Current methods reduce this to O(n^3 m^3), where m < p is the desired degrees of freedom. This computational cost, however, is still prohibitive in many applications. To address this limitation, we present the Orthogonal Linear Mixing Model (OLMM), an MOGP in which exact inference scales linearly in m: O(n^3 m). This advance opens up a wide range of real-world tasks and can be combined with existing GP approximations in a plug-and-play way as demonstrated in the paper. Additionally, the paper organises the existing disparate literature on MOGP models into a simple taxonomy called the Mixing Model Hierarchy (MMH).

A Differentiable Programming System to Bridge Machine Learning and Scientific Computing

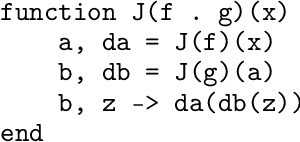
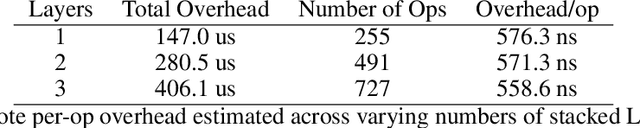
Scientific computing is increasingly incorporating the advancements in machine learning and the ability to work with large amounts of data. At the same time, machine learning models are becoming increasingly sophisticated and exhibit many features often seen in scientific computing, stressing the capabilities of machine learning frameworks. Just as the disciplines of scientific computing and machine learning have shared common underlying infrastructure in the form of numerical linear algebra, we now have the opportunity to further share new computational infrastructure, and thus ideas, in the form of Differentiable Programming. We describe Zygote, a Differentiable Programming system that is able to take gradients of general program structures. We implement this system in the Julia programming language. Our system supports almost all language constructs (control flow, recursion, mutation, etc.) and compiles high-performance code without requiring any user intervention or refactoring to stage computations. This enables an expressive programming model for deep learning, but more importantly, it enables us to incorporate a large ecosystem of libraries in our models in a straightforward way. We discuss our approach to automatic differentiation, including its support for advanced techniques such as mixed-mode, complex and checkpointed differentiation, and present several examples of differentiating programs.

The Gaussian Process Autoregressive Regression Model (GPAR)

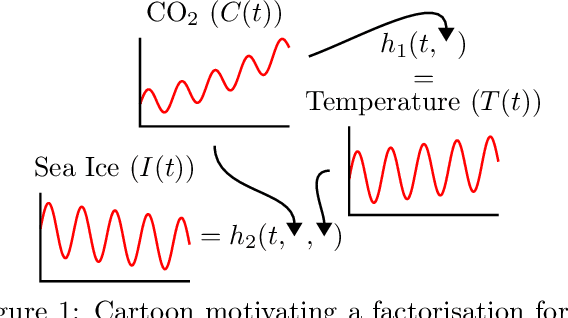
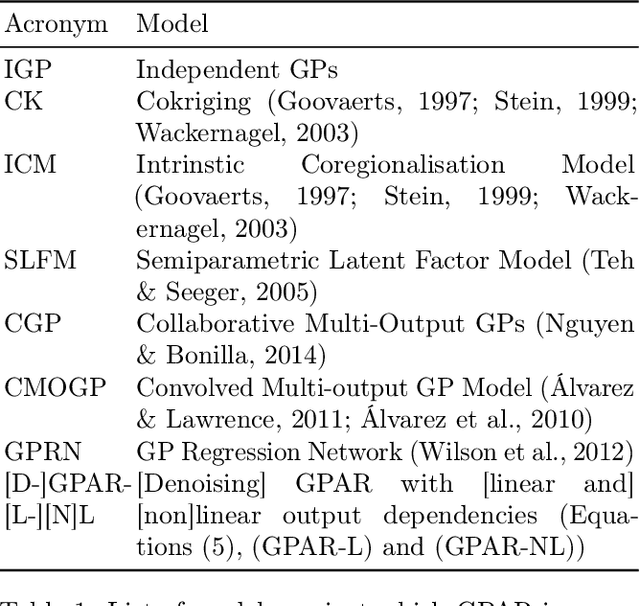
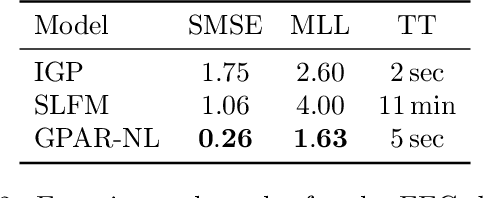
Multi-output regression models must exploit dependencies between outputs to maximise predictive performance. The application of Gaussian processes (GPs) to this setting typically yields models that are computationally demanding and have limited representational power. We present the Gaussian Process Autoregressive Regression (GPAR) model, a scalable multi-output GP model that is able to capture nonlinear, possibly input-varying, dependencies between outputs in a simple and tractable way: the product rule is used to decompose the joint distribution over the outputs into a set of conditionals, each of which is modelled by a standard GP. GPAR's efficacy is demonstrated on a variety of synthetic and real-world problems, outperforming existing GP models and achieving state-of-the-art performance on the tasks with existing benchmarks.