Multiscale Cross-Modal Mapping of Molecular, Pathologic, and Radiologic Phenotypes in Lipid-Deficient Clear Cell Renal CellCarcinoma

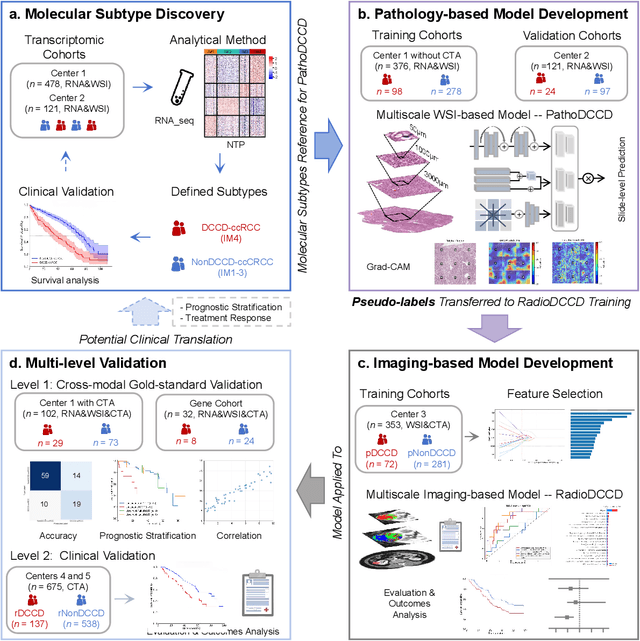
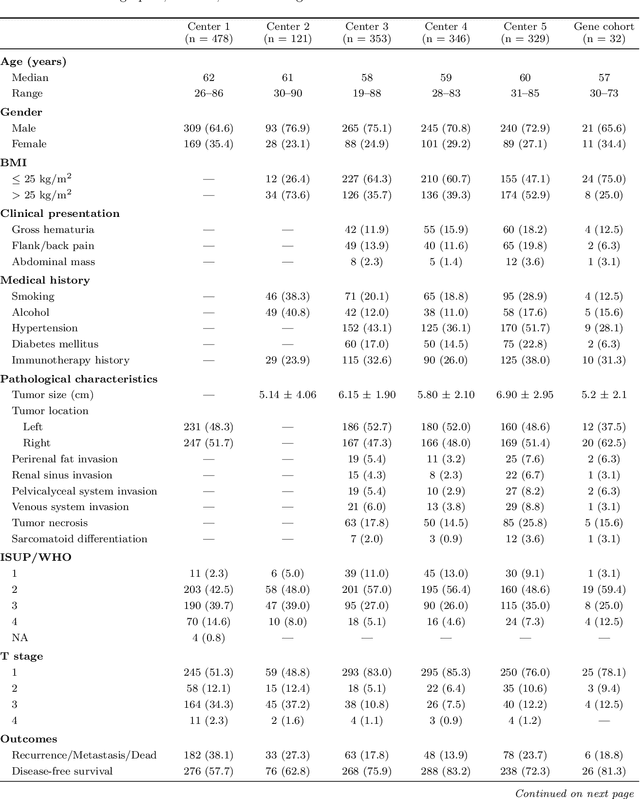
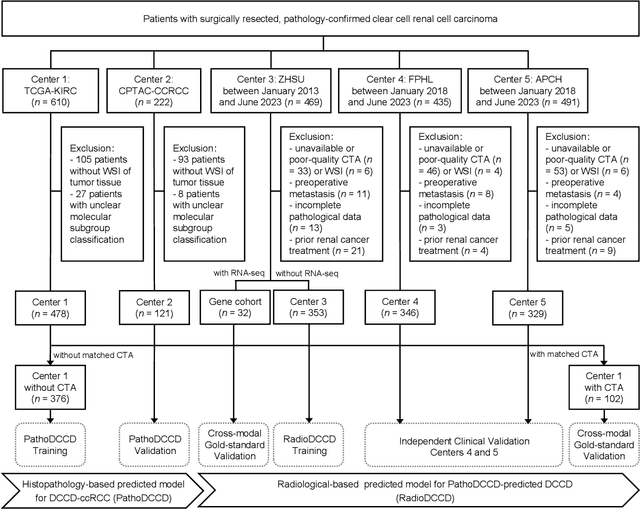
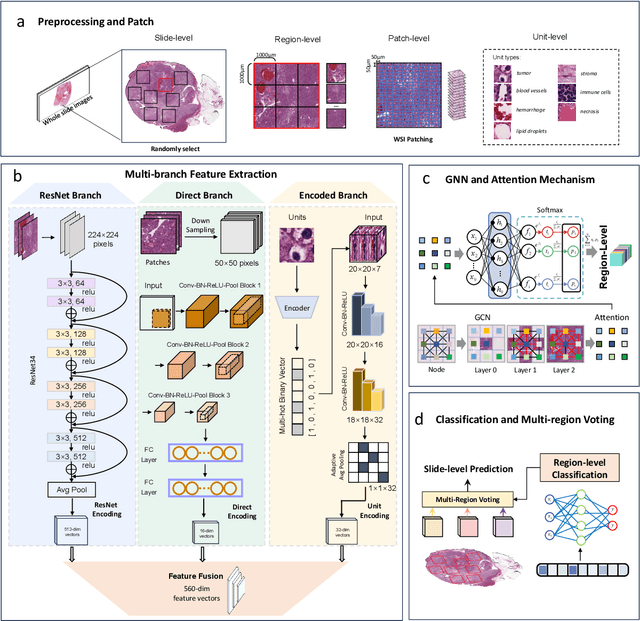
Clear cell renal cell carcinoma (ccRCC) exhibits extensive intratumoral heterogeneity on multiple biological scales, contributing to variable clinical outcomes and limiting the effectiveness of conventional TNM staging, which highlights the urgent need for multiscale integrative analytic frameworks. The lipid-deficient de-clear cell differentiated (DCCD) ccRCC subtype, defined by multi-omics analyses, is associated with adverse outcomes even in early-stage disease. Here, we establish a hierarchical cross-scale framework for the preoperative identification of DCCD-ccRCC. At the highest layer, cross-modal mapping transferred molecular signatures to histological and CT phenotypes, establishing a molecular-to-pathology-to-radiology supervisory bridge. Within this framework, each modality-specific model is designed to mirror the inherent hierarchical structure of tumor biology. PathoDCCD captured multi-scale microscopic features, from cellular morphology and tissue architecture to meso-regional organization. RadioDCCD integrated complementary macroscopic information by combining whole-tumor and its habitat-subregions radiomics with a 2D maximal-section heterogeneity metric. These nested models enabled integrated molecular subtype prediction and clinical risk stratification. Across five cohorts totaling 1,659 patients, PathoDCCD reliably recapitulated molecular subtypes, while RadioDCCD provided reliable preoperative prediction. The consistent predictions identified patients with the poorest clinical outcomes. This cross-scale paradigm unifies molecular biology, computational pathology, and quantitative radiology into a biologically grounded strategy for preoperative noninvasive molecular phenotyping of ccRCC.

Learning Dynamics under Environmental Constraints via Measurement-Induced Bundle Structures

Learning unknown dynamics under environmental (or external) constraints is fundamental to many fields (e.g., modern robotics), particularly challenging when constraint information is only locally available and uncertain. Existing approaches requiring global constraints or using probabilistic filtering fail to fully exploit the geometric structure inherent in local measurements (by using, e.g., sensors) and constraints. This paper presents a geometric framework unifying measurements, constraints, and dynamics learning through a fiber bundle structure over the state space. This naturally induced geometric structure enables measurement-aware Control Barrier Functions that adapt to local sensing (or measurement) conditions. By integrating Neural ODEs, our framework learns continuous-time dynamics while preserving geometric constraints, with theoretical guarantees of learning convergence and constraint satisfaction dependent on sensing quality. The geometric framework not only enables efficient dynamics learning but also suggests promising directions for integration with reinforcement learning approaches. Extensive simulations demonstrate significant improvements in both learning efficiency and constraint satisfaction over traditional methods, especially under limited and uncertain sensing conditions.

Learning and Current Prediction of PMSM Drive via Differential Neural Networks

Learning models for dynamical systems in continuous time is significant for understanding complex phenomena and making accurate predictions. This study presents a novel approach utilizing differential neural networks (DNNs) to model nonlinear systems, specifically permanent magnet synchronous motors (PMSMs), and to predict their current trajectories. The efficacy of our approach is validated through experiments conducted under various load disturbances and no-load conditions. The results demonstrate that our method effectively and accurately reconstructs the original systems, showcasing strong short-term and long-term prediction capabilities and robustness. This study provides valuable insights into learning the inherent dynamics of complex dynamical data and holds potential for further applications in fields such as weather forecasting, robotics, and collective behavior analysis.

ICODE: Modeling Dynamical Systems with Extrinsic Input Information

Learning models of dynamical systems with external inputs, that may be, for example, nonsmooth or piecewise, is crucial for studying complex phenomena and predicting future state evolution, which is essential for applications such as safety guarantees and decision-making. In this work, we introduce \emph{Input Concomitant Neural ODEs (ICODEs)}, which incorporate precise real-time input information into the learning process of the models, rather than treating the inputs as hidden parameters to be learned. The sufficient conditions to ensure the model's contraction property are provided to guarantee that system trajectories of the trained model converge to a fixed point, regardless of initial conditions across different training processes. We validate our method through experiments on several representative real dynamics: Single-link robot, DC-to-DC converter, motion dynamics of a rigid body, Rabinovich-Fabrikant equation, Glycolytic-glycogenolytic pathway model, and heat conduction equation. The experimental results demonstrate that our proposed ICODEs efficiently learn the ground truth systems, achieving superior prediction performance under both typical and atypical inputs. This work offers a valuable class of neural ODE models for understanding physical systems with explicit external input information, with potential promising applications in fields such as physics and robotics.

ControlSynth Neural ODEs: Modeling Dynamical Systems with Guaranteed Convergence

Neural ODEs (NODEs) are continuous-time neural networks (NNs) that can process data without the limitation of time intervals. They have advantages in learning and understanding the evolution of complex real dynamics. Many previous works have focused on NODEs in concise forms, while numerous physical systems taking straightforward forms, in fact, belong to their more complex quasi-classes, thus appealing to a class of general NODEs with high scalability and flexibility to model those systems. This, however, may result in intricate nonlinear properties. In this paper, we introduce ControlSynth Neural ODEs (CSODEs). We show that despite their highly nonlinear nature, convergence can be guaranteed via tractable linear inequalities. In the composition of CSODEs, we introduce an extra control term for learning the potential simultaneous capture of dynamics at different scales, which could be particularly useful for partial differential equation-formulated systems. Finally, we compare several representative NNs with CSODEs on important physical dynamics under the inductive biases of CSODEs, and illustrate that CSODEs have better learning and predictive abilities in these settings.