Adaptive Forests For Classification

Random Forests (RF) and Extreme Gradient Boosting (XGBoost) are two of the most widely used and highly performing classification and regression models. They aggregate equally weighted CART trees, generated randomly in RF or sequentially in XGBoost. In this paper, we propose Adaptive Forests (AF), a novel approach that adaptively selects the weights of the underlying CART models. AF combines (a) the Optimal Predictive-Policy Trees (OP2T) framework to prescribe tailored, input-dependent unequal weights to trees and (b) Mixed Integer Optimization (MIO) to refine weight candidates dynamically, enhancing overall performance. We demonstrate that AF consistently outperforms RF, XGBoost, and other weighted RF in binary and multi-class classification problems over 20+ real-world datasets.

Minimum Cost Adaptive Submodular Cover

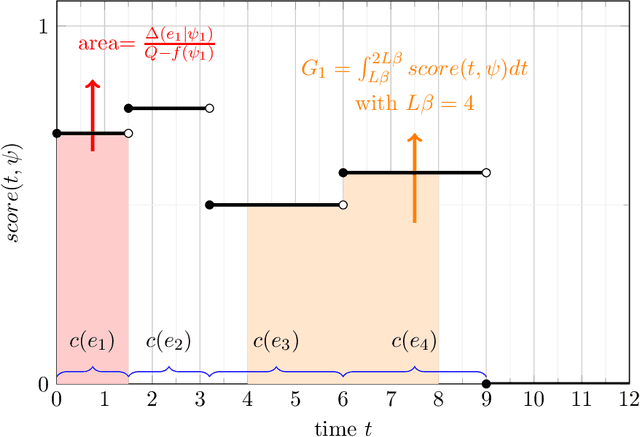
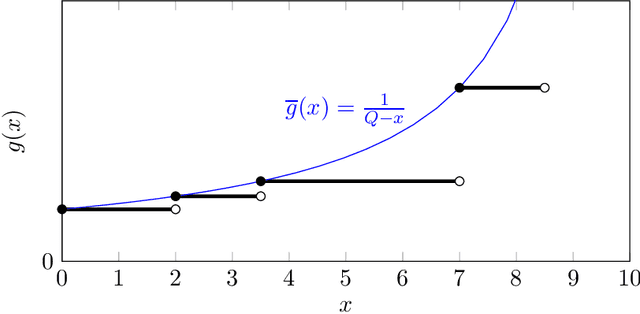
We consider the problem of minimum cost cover of adaptive-submodular functions, and provide a 4(ln Q+1)-approximation algorithm, where Q is the goal value. This bound is nearly the best possible as the problem does not admit any approximation ratio better than ln Q (unless P=NP). Our result is the first O(ln Q)-approximation algorithm for this problem. Previously, O(ln Q) approximation algorithms were only known assuming either independent items or unit-cost items. Furthermore, our result easily extends to the setting where one wants to simultaneously cover multiple adaptive-submodular functions: we obtain the first approximation algorithm for this generalization.