BloombergGPT: A Large Language Model for Finance

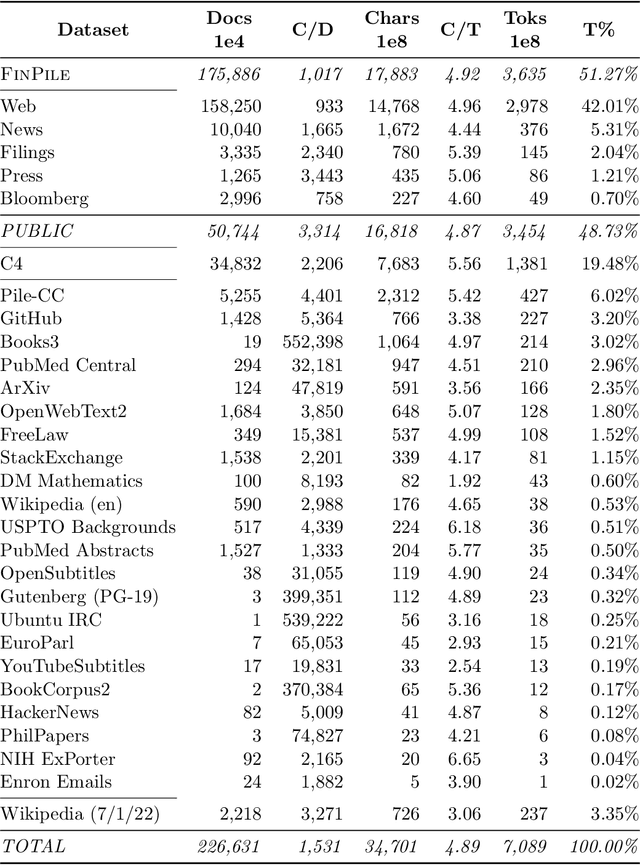
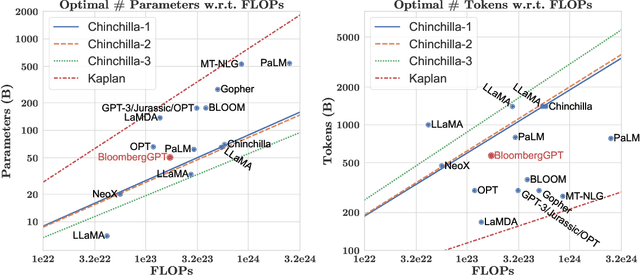
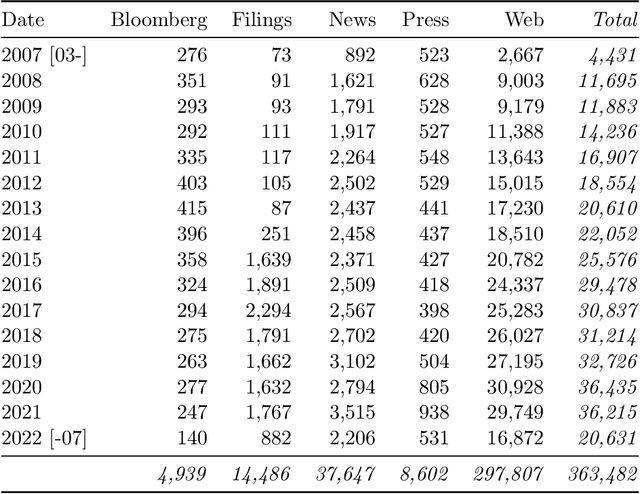
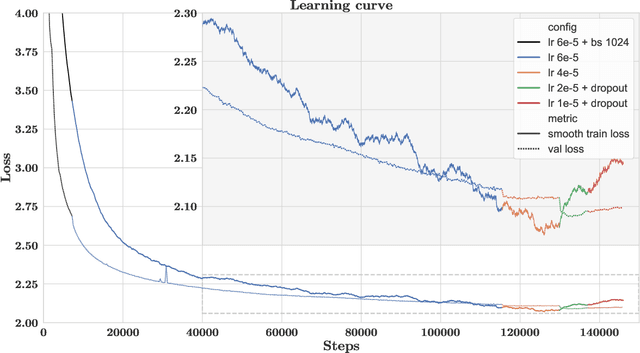
The use of NLP in the realm of financial technology is broad and complex, with applications ranging from sentiment analysis and named entity recognition to question answering. Large Language Models (LLMs) have been shown to be effective on a variety of tasks; however, no LLM specialized for the financial domain has been reported in literature. In this work, we present BloombergGPT, a 50 billion parameter language model that is trained on a wide range of financial data. We construct a 363 billion token dataset based on Bloomberg's extensive data sources, perhaps the largest domain-specific dataset yet, augmented with 345 billion tokens from general purpose datasets. We validate BloombergGPT on standard LLM benchmarks, open financial benchmarks, and a suite of internal benchmarks that most accurately reflect our intended usage. Our mixed dataset training leads to a model that outperforms existing models on financial tasks by significant margins without sacrificing performance on general LLM benchmarks. Additionally, we explain our modeling choices, training process, and evaluation methodology. As a next step, we plan to release training logs (Chronicles) detailing our experience in training BloombergGPT.

Weakly-supervised Contextualization of Knowledge Graph Facts

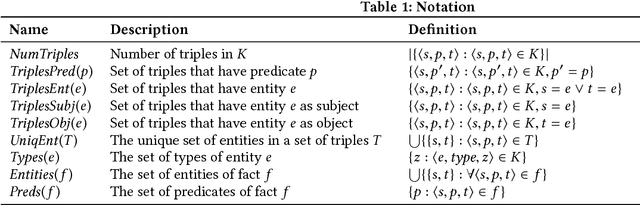
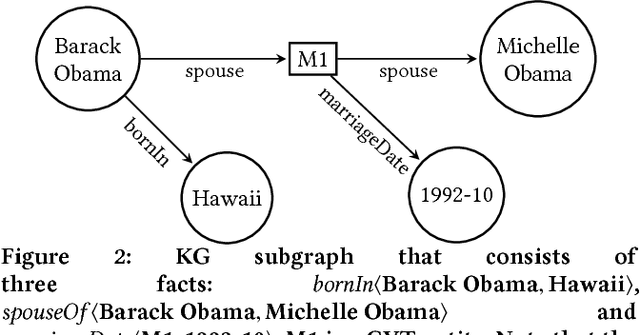
Knowledge graphs (KGs) model facts about the world, they consist of nodes (entities such as companies and people) that are connected by edges (relations such as founderOf). Facts encoded in KGs are frequently used by search applications to augment result pages. When presenting a KG fact to the user, providing other facts that are pertinent to that main fact can enrich the user experience and support exploratory information needs. KG fact contextualization is the task of augmenting a given KG fact with additional and useful KG facts. The task is challenging because of the large size of KGs, discovering other relevant facts even in a small neighborhood of the given fact results in an enormous amount of candidates. We introduce a neural fact contextualization method (NFCM) to address the KG fact contextualization task. NFCM first generates a set of candidate facts in the neighborhood of a given fact and then ranks the candidate facts using a supervised learning to rank model. The ranking model combines features that we automatically learn from data and that represent the query-candidate facts with a set of hand-crafted features we devised or adjusted for this task. In order to obtain the annotations required to train the learning to rank model at scale, we generate training data automatically using distant supervision on a large entity-tagged text corpus. We show that ranking functions learned on this data are effective at contextualizing KG facts. Evaluation using human assessors shows that it significantly outperforms several competitive baselines.

Faster Greedy MAP Inference for Determinantal Point Processes

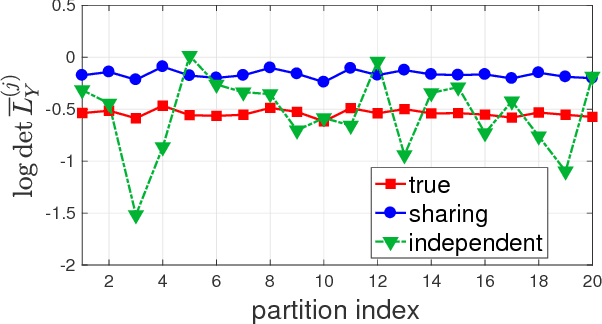
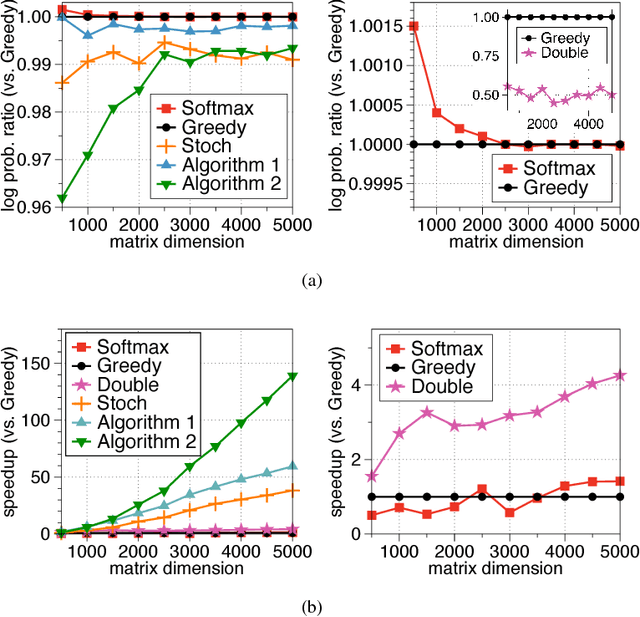
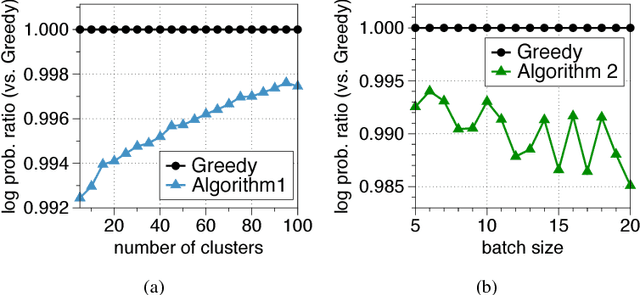
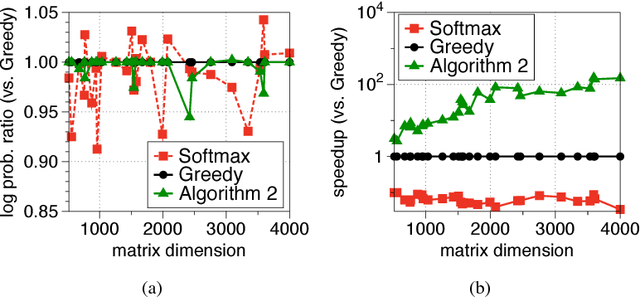
Determinantal point processes (DPPs) are popular probabilistic models that arise in many machine learning tasks, where distributions of diverse sets are characterized by matrix determinants. In this paper, we develop fast algorithms to find the most likely configuration (MAP) of large-scale DPPs, which is NP-hard in general. Due to the submodular nature of the MAP objective, greedy algorithms have been used with empirical success. Greedy implementations require computation of log-determinants, matrix inverses or solving linear systems at each iteration. We present faster implementations of the greedy algorithms by utilizing the complementary benefits of two log-determinant approximation schemes: (a) first-order expansions to the matrix log-determinant function and (b) high-order expansions to the scalar log function with stochastic trace estimators. In our experiments, our algorithms are orders of magnitude faster than their competitors, while sacrificing marginal accuracy.

Adaptive Submodular Ranking

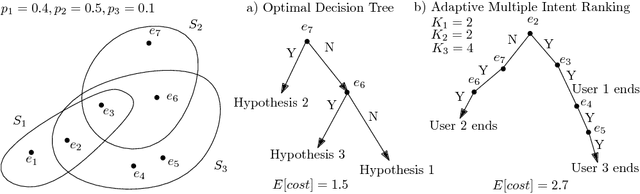
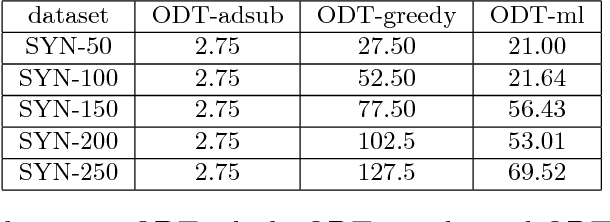
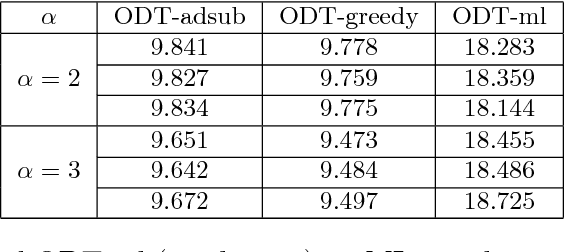
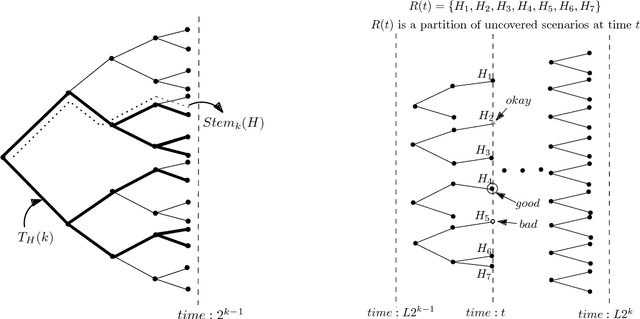
We study a general adaptive ranking problem where an algorithm needs to perform a sequence of actions on a random user, drawn from a known distribution, so as to "satisfy" the user as early as possible. The satisfaction of each user is captured by an individual submodular function, where the user is said to be satisfied when the function value goes above some threshold. We obtain a logarithmic factor approximation algorithm for this adaptive ranking problem, which is the best possible. The adaptive ranking problem has many applications in active learning and ranking: it significantly generalizes previously-studied problems such as optimal decision trees, equivalence class determination, decision region determination and submodular cover. We also present some preliminary experimental results based on our algorithm.

Spectral Clustering via the Power Method -- Provably

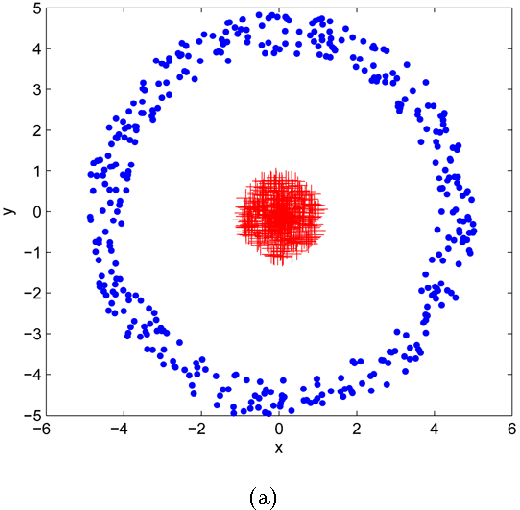
Spectral clustering is one of the most important algorithms in data mining and machine intelligence; however, its computational complexity limits its application to truly large scale data analysis. The computational bottleneck in spectral clustering is computing a few of the top eigenvectors of the (normalized) Laplacian matrix corresponding to the graph representing the data to be clustered. One way to speed up the computation of these eigenvectors is to use the "power method" from the numerical linear algebra literature. Although the power method has been empirically used to speed up spectral clustering, the theory behind this approach, to the best of our knowledge, remains unexplored. This paper provides the \emph{first} such rigorous theoretical justification, arguing that a small number of power iterations suffices to obtain near-optimal partitionings using the approximate eigenvectors. Specifically, we prove that solving the $k$-means clustering problem on the approximate eigenvectors obtained via the power method gives an additive-error approximation to solving the $k$-means problem on the optimal eigenvectors.

Fast Conical Hull Algorithms for Near-separable Non-negative Matrix Factorization

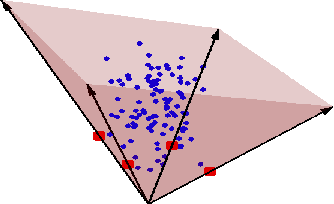
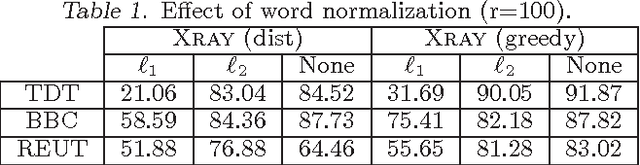
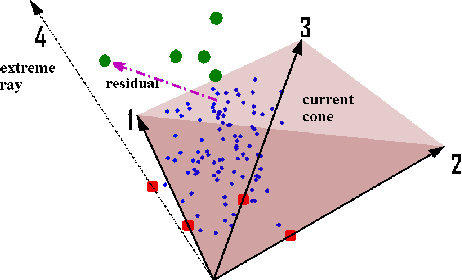
The separability assumption (Donoho & Stodden, 2003; Arora et al., 2012) turns non-negative matrix factorization (NMF) into a tractable problem. Recently, a new class of provably-correct NMF algorithms have emerged under this assumption. In this paper, we reformulate the separable NMF problem as that of finding the extreme rays of the conical hull of a finite set of vectors. From this geometric perspective, we derive new separable NMF algorithms that are highly scalable and empirically noise robust, and have several other favorable properties in relation to existing methods. A parallel implementation of our algorithm demonstrates high scalability on shared- and distributed-memory machines.