agriFrame: Agricultural framework to remotely control a rover inside a greenhouse environment

The growing demand for innovation in agriculture is essential for food security worldwide and more implicit in developing countries. With growing demand comes a reduction in rapid development time. Data collection and analysis are essential in agriculture. However, considering a given crop, its cycle comes once a year, and researchers must wait a few months before collecting more data for the given crop. To overcome this hurdle, researchers are venturing into digital twins for agriculture. Toward this effort, we present an agricultural framework(agriFrame). Here, we introduce a simulated greenhouse environment for testing and controlling a robot and remotely controlling/implementing the algorithms in the real-world greenhouse setup. This work showcases the importance/interdependence of network setup, remotely controllable rover, and messaging protocol. The sophisticated yet simple-to-use agriFrame has been optimized for the simulator on minimal laptop/desktop specifications.

Beyond Discretization: Learning the Optimal Solution Path

Many applications require minimizing a family of optimization problems indexed by some hyperparameter $\lambda \in \Lambda$ to obtain an entire solution path. Traditional approaches proceed by discretizing $\Lambda$ and solving a series of optimization problems. We propose an alternative approach that parameterizes the solution path with a set of basis functions and solves a \emph{single} stochastic optimization problem to learn the entire solution path. Our method offers substantial complexity improvements over discretization. When using constant-step size SGD, the uniform error of our learned solution path relative to the true path exhibits linear convergence to a constant related to the expressiveness of the basis. When the true solution path lies in the span of the basis, this constant is zero. We also prove stronger results for special cases common in machine learning: When $\lambda \in [-1, 1]$ and the solution path is $\nu$-times differentiable, constant step-size SGD learns a path with $\epsilon$ uniform error after at most $O(\epsilon^{\frac{1}{1-\nu}} \log(1/\epsilon))$ iterations, and when the solution path is analytic, it only requires $O\left(\log^2(1/\epsilon)\log\log(1/\epsilon)\right)$. By comparison, the best-known discretization schemes in these settings require at least $O(\epsilon^{-1/2})$ discretization points (and even more gradient calls). Finally, we propose an adaptive variant of our method that sequentially adds basis functions and demonstrates strong numerical performance through experiments.

Learning Best-in-Class Policies for the Predict-then-Optimize Framework

We propose a novel family of decision-aware surrogate losses, called Perturbation Gradient (PG) losses, for the predict-then-optimize framework. These losses directly approximate the downstream decision loss and can be optimized using off-the-shelf gradient-based methods. Importantly, unlike existing surrogate losses, the approximation error of our PG losses vanishes as the number of samples grows. This implies that optimizing our surrogate loss yields a best-in-class policy asymptotically, even in misspecified settings. This is the first such result in misspecified settings and we provide numerical evidence confirming our PG losses substantively outperform existing proposals when the underlying model is misspecified and the noise is not centrally symmetric. Insofar as misspecification is commonplace in practice -- especially when we might prefer a simpler, more interpretable model -- PG losses offer a novel, theoretically justified, method for computationally tractable decision-aware learning.

Balanced Off-Policy Evaluation for Personalized Pricing

We consider a personalized pricing problem in which we have data consisting of feature information, historical pricing decisions, and binary realized demand. The goal is to perform off-policy evaluation for a new personalized pricing policy that maps features to prices. Methods based on inverse propensity weighting (including doubly robust methods) for off-policy evaluation may perform poorly when the logging policy has little exploration or is deterministic, which is common in pricing applications. Building on the balanced policy evaluation framework of Kallus (2018), we propose a new approach tailored to pricing applications. The key idea is to compute an estimate that minimizes the worst-case mean squared error or maximizes a worst-case lower bound on policy performance, where in both cases the worst-case is taken with respect to a set of possible revenue functions. We establish theoretical convergence guarantees and empirically demonstrate the advantage of our approach using a real-world pricing dataset.

ETA Prediction with Graph Neural Networks in Google Maps

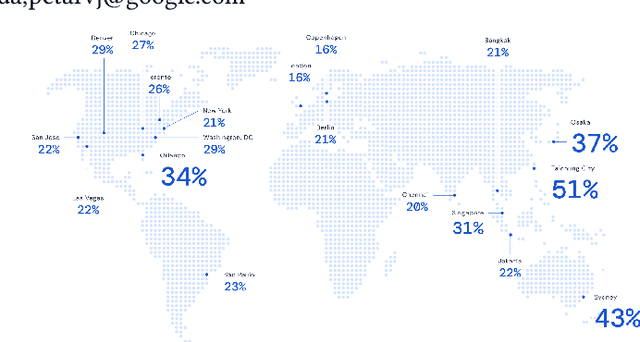
Travel-time prediction constitutes a task of high importance in transportation networks, with web mapping services like Google Maps regularly serving vast quantities of travel time queries from users and enterprises alike. Further, such a task requires accounting for complex spatiotemporal interactions (modelling both the topological properties of the road network and anticipating events -- such as rush hours -- that may occur in the future). Hence, it is an ideal target for graph representation learning at scale. Here we present a graph neural network estimator for estimated time of arrival (ETA) which we have deployed in production at Google Maps. While our main architecture consists of standard GNN building blocks, we further detail the usage of training schedule methods such as MetaGradients in order to make our model robust and production-ready. We also provide prescriptive studies: ablating on various architectural decisions and training regimes, and qualitative analyses on real-world situations where our model provides a competitive edge. Our GNN proved powerful when deployed, significantly reducing negative ETA outcomes in several regions compared to the previous production baseline (40+% in cities like Sydney).

Debiasing In-Sample Policy Performance for Small-Data, Large-Scale Optimization

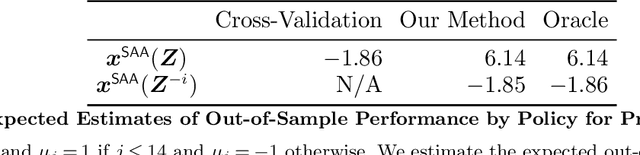
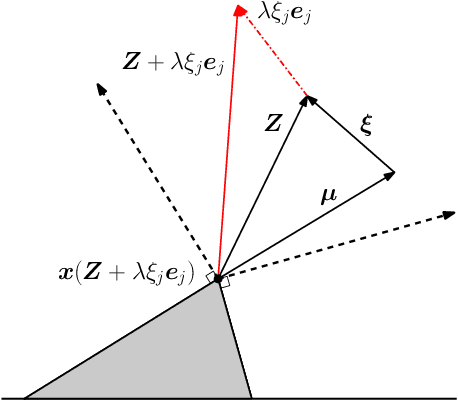
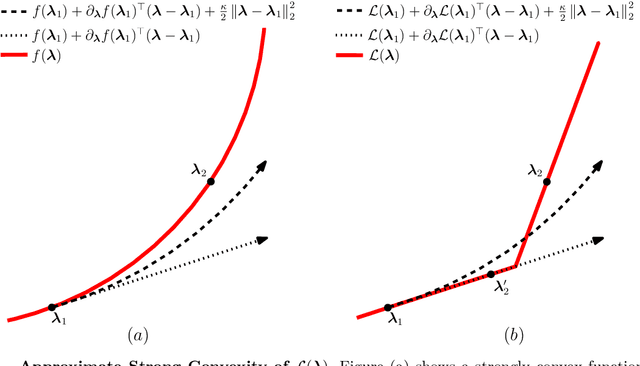
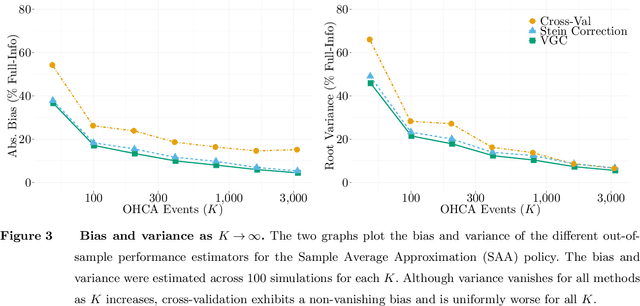
Motivated by the poor performance of cross-validation in settings where data are scarce, we propose a novel estimator of the out-of-sample performance of a policy in data-driven optimization.Our approach exploits the optimization problem's sensitivity analysis to estimate the gradient of the optimal objective value with respect to the amount of noise in the data and uses the estimated gradient to debias the policy's in-sample performance. Unlike cross-validation techniques, our approach avoids sacrificing data for a test set, utilizes all data when training and, hence, is well-suited to settings where data are scarce. We prove bounds on the bias and variance of our estimator for optimization problems with uncertain linear objectives but known, potentially non-convex, feasible regions. For more specialized optimization problems where the feasible region is "weakly-coupled" in a certain sense, we prove stronger results. Specifically, we provide explicit high-probability bounds on the error of our estimator that hold uniformly over a policy class and depends on the problem's dimension and policy class's complexity. Our bounds show that under mild conditions, the error of our estimator vanishes as the dimension of the optimization problem grows, even if the amount of available data remains small and constant. Said differently, we prove our estimator performs well in the small-data, large-scale regime. Finally, we numerically compare our proposed method to state-of-the-art approaches through a case-study on dispatching emergency medical response services using real data. Our method provides more accurate estimates of out-of-sample performance and learns better-performing policies.

Balance Regularized Neural Network Models for Causal Effect Estimation

Estimating individual and average treatment effects from observational data is an important problem in many domains such as healthcare and e-commerce. In this paper, we advocate balance regularization of multi-head neural network architectures. Our work is motivated by representation learning techniques to reduce differences between treated and untreated distributions that potentially arise due to confounding factors. We further regularize the model by encouraging it to predict control outcomes for individuals in the treatment group that are similar to control outcomes in the control group. We empirically study the bias-variance trade-off between different weightings of the regularizers, as well as between inductive and transductive inference.

Data-Pooling in Stochastic Optimization

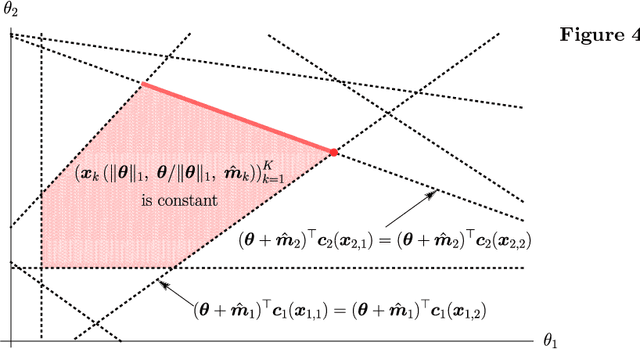
Managing large-scale systems often involves simultaneously solving thousands of unrelated stochastic optimization problems, each with limited data. Intuition suggests one can decouple these unrelated problems and solve them separately without loss of generality. We propose a novel data-pooling algorithm called Shrunken-SAA that disproves this intuition. In particular, we prove that combining data across problems can outperform decoupling, even when there is no a priori structure linking the problems and data are drawn independently. Our approach does not require strong distributional assumptions and applies to constrained, possibly non-convex, non-smooth optimization problems such as vehicle-routing, economic lot-sizing or facility location. We compare and contrast our results to a similar phenomenon in statistics (Stein's Phenomenon), highlighting unique features that arise in the optimization setting that are not present in estimation. We further prove that as the number of problems grows large, Shrunken-SAA learns if pooling can improve upon decoupling and the optimal amount to pool, even if the average amount of data per problem is fixed and bounded. Importantly, we highlight a simple intuition based on stability that highlights when} and why data-pooling offers a benefit, elucidating this perhaps surprising phenomenon. This intuition further suggests that data-pooling offers the most benefits when there are many problems, each of which has a small amount of relevant data. Finally, we demonstrate the practical benefits of data-pooling using real data from a chain of retail drug stores in the context of inventory management.

A Comparison of Monte Carlo Tree Search and Mathematical Optimization for Large Scale Dynamic Resource Allocation

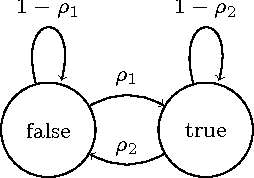
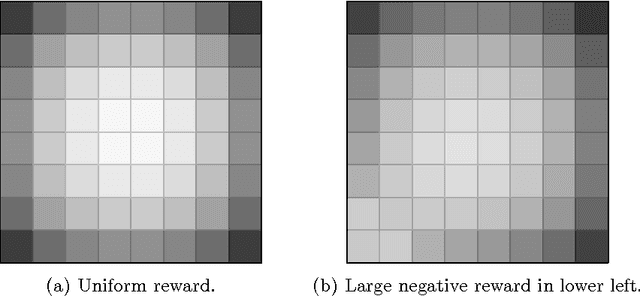
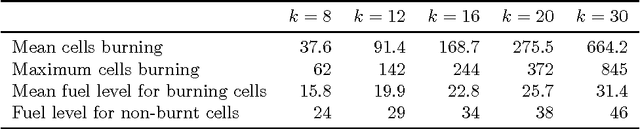
Dynamic resource allocation (DRA) problems are an important class of dynamic stochastic optimization problems that arise in a variety of important real-world applications. DRA problems are notoriously difficult to solve to optimality since they frequently combine stochastic elements with intractably large state and action spaces. Although the artificial intelligence and operations research communities have independently proposed two successful frameworks for solving dynamic stochastic optimization problems---Monte Carlo tree search (MCTS) and mathematical optimization (MO), respectively---the relative merits of these two approaches are not well understood. In this paper, we adapt both MCTS and MO to a problem inspired by tactical wildfire and management and undertake an extensive computational study comparing the two methods on large scale instances in terms of both the state and the action spaces. We show that both methods are able to greatly improve on a baseline, problem-specific heuristic. On smaller instances, the MCTS and MO approaches perform comparably, but the MO approach outperforms MCTS as the size of the problem increases for a fixed computational budget.