Estimate-Then-Optimize Versus Integrated-Estimation-Optimization: A Stochastic Dominance Perspective

In data-driven stochastic optimization, model parameters of the underlying distribution need to be estimated from data in addition to the optimization task. Recent literature suggests the integration of the estimation and optimization processes, by selecting model parameters that lead to the best empirical objective performance. Such an integrated approach can be readily shown to outperform simple ``estimate then optimize" when the model is misspecified. In this paper, we argue that when the model class is rich enough to cover the ground truth, the performance ordering between the two approaches is reversed for nonlinear problems in a strong sense. Simple ``estimate then optimize" outperforms the integrated approach in terms of stochastic dominance of the asymptotic optimality gap, i,e, the mean, all other moments, and the entire asymptotic distribution of the optimality gap is always better. Analogous results also hold under constrained settings and when contextual features are available. We also provide experimental findings to support our theory.

Balanced Off-Policy Evaluation for Personalized Pricing

We consider a personalized pricing problem in which we have data consisting of feature information, historical pricing decisions, and binary realized demand. The goal is to perform off-policy evaluation for a new personalized pricing policy that maps features to prices. Methods based on inverse propensity weighting (including doubly robust methods) for off-policy evaluation may perform poorly when the logging policy has little exploration or is deterministic, which is common in pricing applications. Building on the balanced policy evaluation framework of Kallus (2018), we propose a new approach tailored to pricing applications. The key idea is to compute an estimate that minimizes the worst-case mean squared error or maximizes a worst-case lower bound on policy performance, where in both cases the worst-case is taken with respect to a set of possible revenue functions. We establish theoretical convergence guarantees and empirically demonstrate the advantage of our approach using a real-world pricing dataset.

Decision Trees for Decision-Making under the Predict-then-Optimize Framework

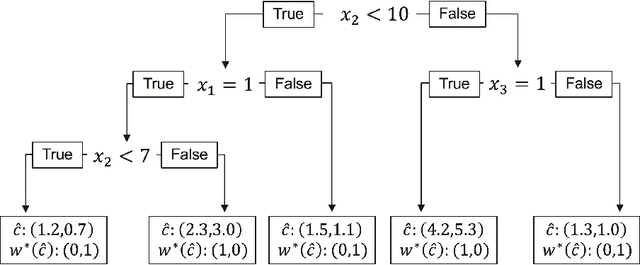
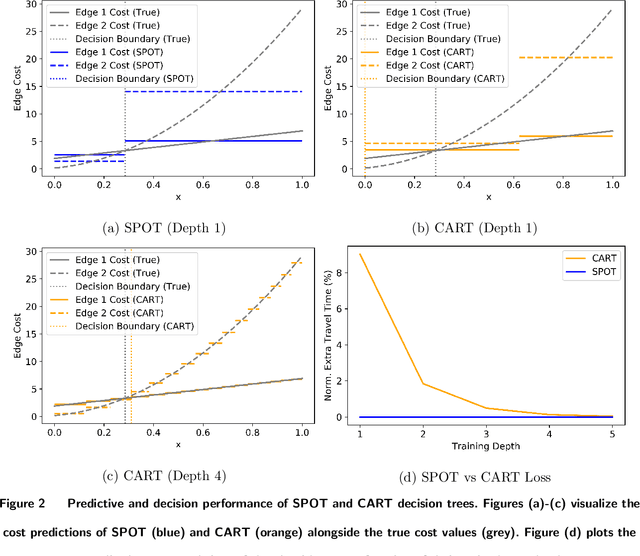
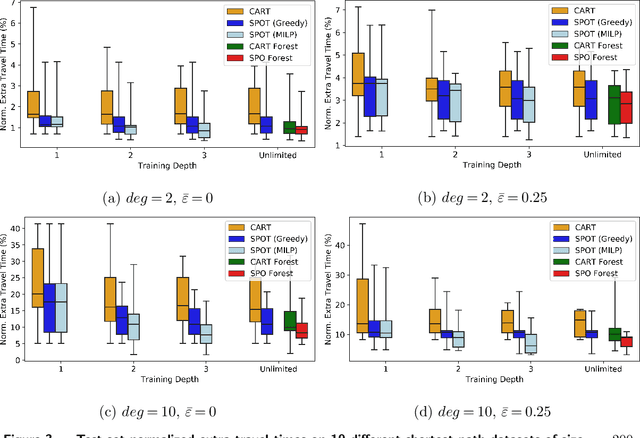
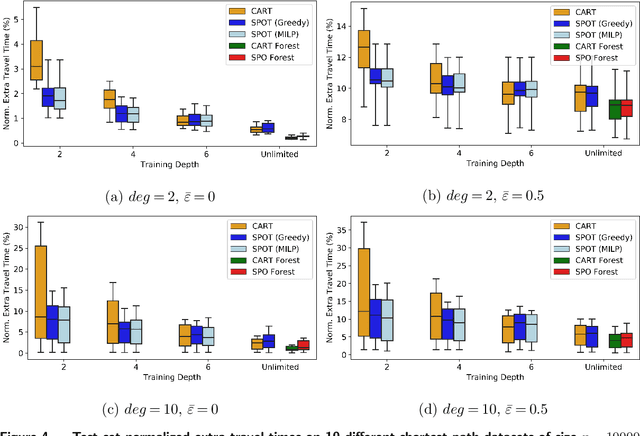
We consider the use of decision trees for decision-making problems under the predict-then-optimize framework. That is, we would like to first use a decision tree to predict unknown input parameters of an optimization problem, and then make decisions by solving the optimization problem using the predicted parameters. A natural loss function in this framework is to measure the suboptimality of the decisions induced by the predicted input parameters, as opposed to measuring loss using input parameter prediction error. This natural loss function is known in the literature as the Smart Predict-then-Optimize (SPO) loss, and we propose a tractable methodology called SPO Trees (SPOTs) for training decision trees under this loss. SPOTs benefit from the interpretability of decision trees, providing an interpretable segmentation of contextual features into groups with distinct optimal solutions to the optimization problem of interest. We conduct several numerical experiments on synthetic and real data including the prediction of travel times for shortest path problems and predicting click probabilities for news article recommendation. We demonstrate on these datasets that SPOTs simultaneously provide higher quality decisions and significantly lower model complexity than other machine learning approaches (e.g., CART) trained to minimize prediction error.

Generalization Bounds in the Predict-then-Optimize Framework

The predict-then-optimize framework is fundamental in many practical settings: predict the unknown parameters of an optimization problem, and then solve the problem using the predicted values of the parameters. A natural loss function in this environment is to consider the cost of the decisions induced by the predicted parameters, in contrast to the prediction error of the parameters. This loss function was recently introduced in Elmachtoub and Grigas (2017), which called it the Smart Predict-then-Optimize (SPO) loss. Since the SPO loss is nonconvex and noncontinuous, standard results for deriving generalization bounds do not apply. In this work, we provide an assortment of generalization bounds for the SPO loss function. In particular, we derive bounds based on the Natarajan dimension that, in the case of a polyhedral feasible region, scale at most logarithmically in the number of extreme points, but, in the case of a general convex set, have poor dependence on the dimension. By exploiting the structure of the SPO loss function and an additional strong convexity assumption on the feasible region, we can dramatically improve the dependence on the dimension via an analysis and corresponding bounds that are akin to the margin guarantees in classification problems.

A Practical Method for Solving Contextual Bandit Problems Using Decision Trees

Many efficient algorithms with strong theoretical guarantees have been proposed for the contextual multi-armed bandit problem. However, applying these algorithms in practice can be difficult because they require domain expertise to build appropriate features and to tune their parameters. We propose a new method for the contextual bandit problem that is simple, practical, and can be applied with little or no domain expertise. Our algorithm relies on decision trees to model the context-reward relationship. Decision trees are non-parametric, interpretable, and work well without hand-crafted features. To guide the exploration-exploitation trade-off, we use a bootstrapping approach which abstracts Thompson sampling to non-Bayesian settings. We also discuss several computational heuristics and demonstrate the performance of our method on several datasets.

Smart "Predict, then Optimize"

Many real-world analytics problems involve two significant challenges: prediction and optimization. Due to the typically complex nature of each challenge, the standard paradigm is to predict, then optimize. By and large, machine learning tools are intended to minimize prediction error and do not account for how the predictions will be used in a downstream optimization problem. In contrast, we propose a new and very general framework, called Smart "Predict, then Optimize" (SPO), which directly leverages the optimization problem structure, i.e., its objective and constraints, for designing successful analytics tools. A key component of our framework is the SPO loss function, which measures the quality of a prediction by comparing the objective values of the solutions generated using the predicted and observed parameters, respectively. Training a model with respect to the SPO loss is computationally challenging, and therefore we also develop a surrogate loss function, called the SPO+ loss, which upper bounds the SPO loss, has desirable convexity properties, and is statistically consistent under mild conditions. We also propose a stochastic gradient descent algorithm which allows for situations in which the number of training samples is large, model regularization is desired, and/or the optimization problem of interest is nonlinear or integer. Finally, we perform computational experiments to empirically verify the success of our SPO framework in comparison to the standard predict-then-optimize approach.