MC2G: An Efficient Algorithm for Matrix Completion with Social and Item Similarity Graphs

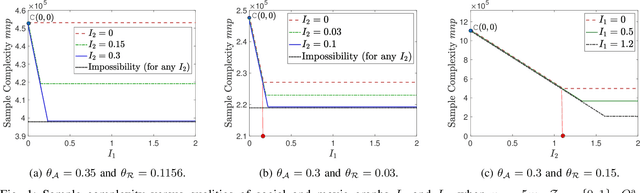
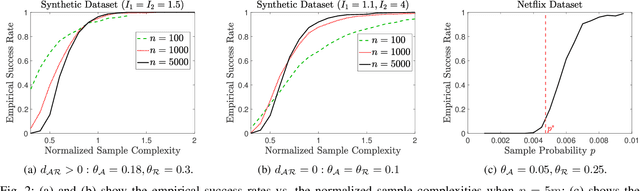
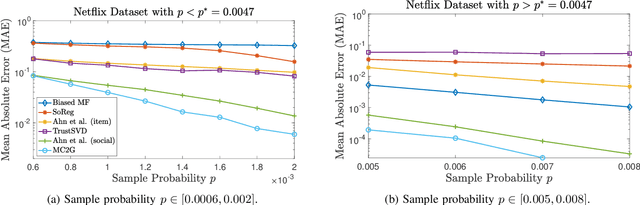
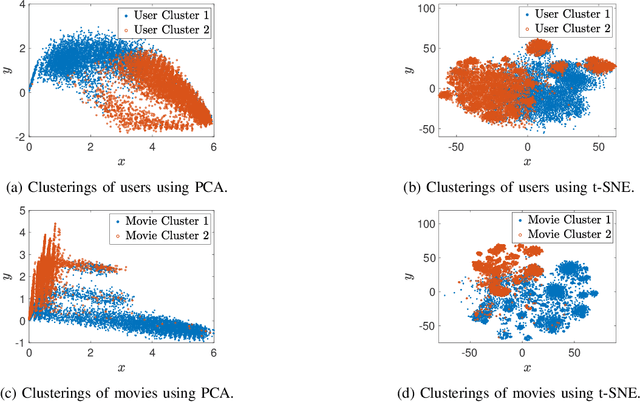
We consider a discrete-valued matrix completion problem for recommender systems in which both the social and item similarity graphs are available as side information. We develop and analyze MC2G (Matrix Completion with 2 Graphs), a quasilinear-time algorithm which is based on spectral clustering and local refinement steps. We show that the sample complexity of MC2G meets an information-theoretic limit that is derived using maximum likelihood estimation and is also order-optimal. We demonstrate that having both graphs as side information outperforms having just a single graph, thus the availability of two graphs results in a synergistic effect. Experiments on synthetic datasets corroborate our theoretical results. Finally, experiments on a sub-sampled version of the Netflix dataset show that MC2G significantly outperforms other state-of-the-art matrix completion algorithms that leverage graph side information.

Exact Asymptotics for Learning Tree-Structured Graphical Models with Side Information: Noiseless and Noisy Samples

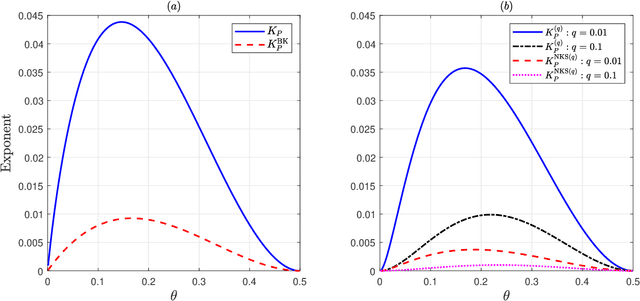
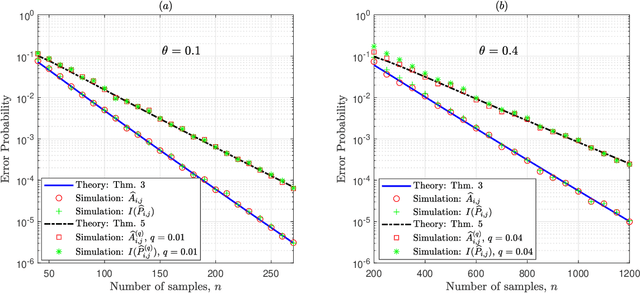
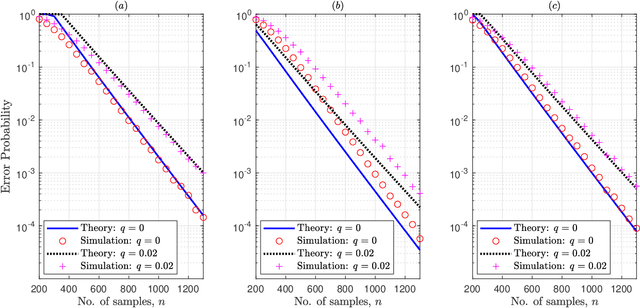
Given side information that an Ising tree-structured graphical model is homogeneous and has no external field, we derive the exact asymptotics of learning its structure from independently drawn samples. Our results, which leverage the use of probabilistic tools from the theory of strong large deviations, refine the large deviation (error exponents) results of Tan, Anandkumar, Tong, and Willsky [IEEE Trans. on Inform. Th., 57(3):1714--1735, 2011] and strictly improve those of Bresler and Karzand [Ann. Statist., 2020]. In addition, we extend our results to the scenario in which the samples are observed in random noise. In this case, we show that they strictly improve on the recent results of Nikolakakis, Kalogerias, and Sarwate [Proc. AISTATS, 1771--1782, 2019]. Our theoretical results demonstrate keen agreement with experimental results for sample sizes as small as that in the hundreds.

Optimal Resolution of Change-Point Detection with Empirically Observed Statistics and Erasures

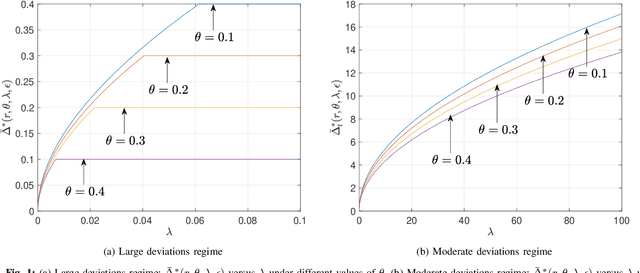
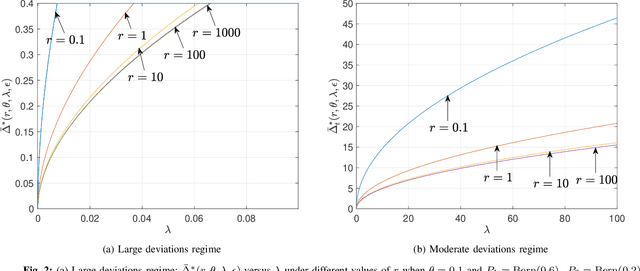
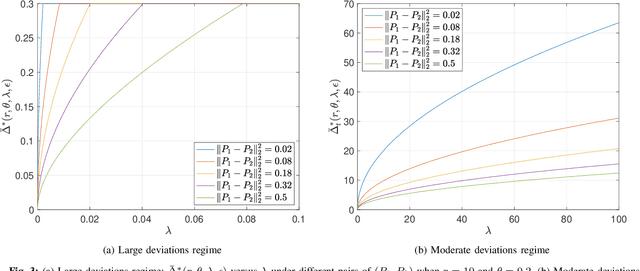
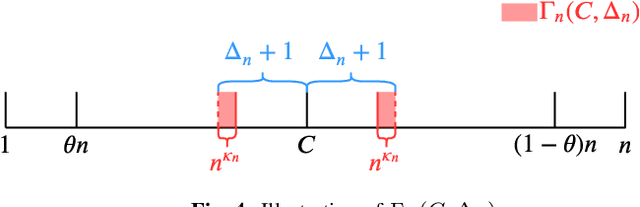
This paper revisits the offline change-point detection problem from a statistical learning perspective. Instead of assuming that the underlying pre- and post-change distributions are known, it is assumed that we have partial knowledge of these distributions based on empirically observed statistics in the form of training sequences. Our problem formulation finds a variety of real-life applications from detecting when climate change occurred to detecting when a virus mutated. Using the training sequences as well as the test sequence consisting of a single-change and allowing for the erasure or rejection option, we derive the optimal resolution between the estimated and true change-points under two different asymptotic regimes on the undetected error probability---namely, the large and moderate deviations regimes. In both regimes, strong converses are also proved. In the moderate deviations case, the optimal resolution is a simple function of a symmetrized version of the chi-square distance.

Thompson Sampling Algorithms for Mean-Variance Bandits

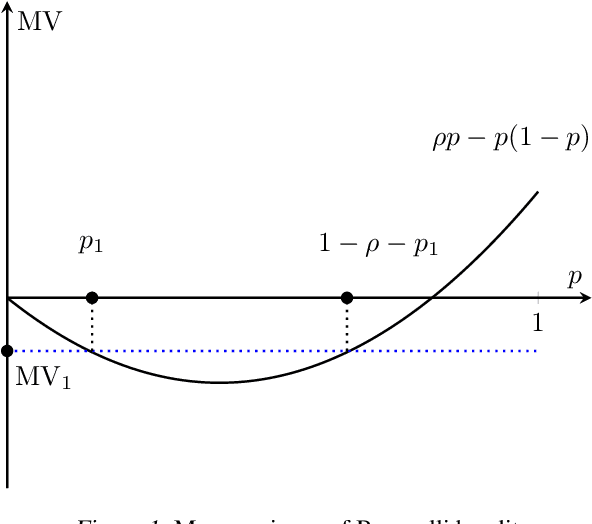
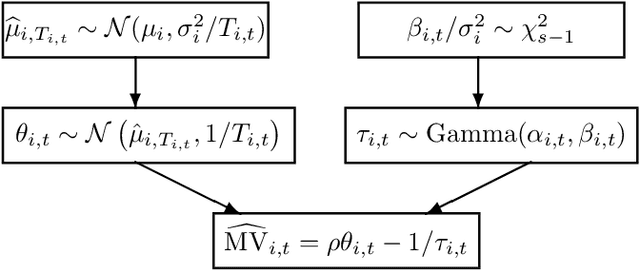
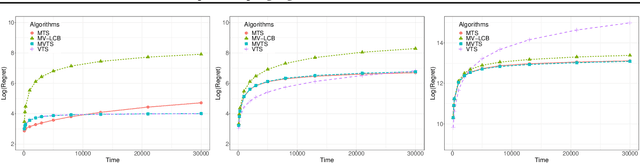
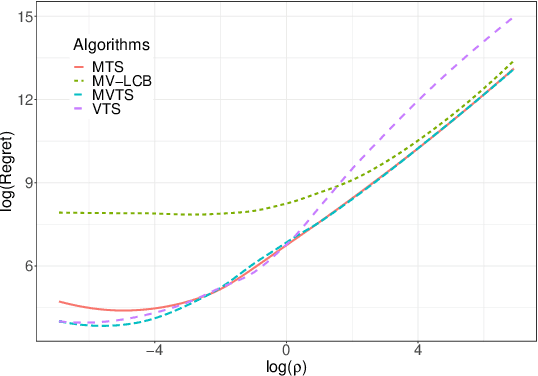
The multi-armed bandit (MAB) problem is a classical learning task that exemplifies the exploration-exploitation tradeoff. However, standard formulations do not take into account risk. In online decision making systems, risk is a primary concern. In this regard, the mean-variance risk measure is one of the most common objective functions. Existing algorithms for mean-variance optimization in the context of MAB problems have unrealistic assumptions on the reward distributions. We develop Thompson Sampling-style algorithms for mean-variance MAB and provide comprehensive regret analyses for Gaussian and Bernoulli bandits with fewer assumptions. Our algorithms achieve the best known regret bounds for mean-variance MABs and also attain the information-theoretic bounds in some parameter regimes. Empirical simulations show that our algorithms significantly outperform existing LCB-based algorithms for all risk tolerances.

Tight Regret Bounds for Noisy Optimization of a Brownian Motion

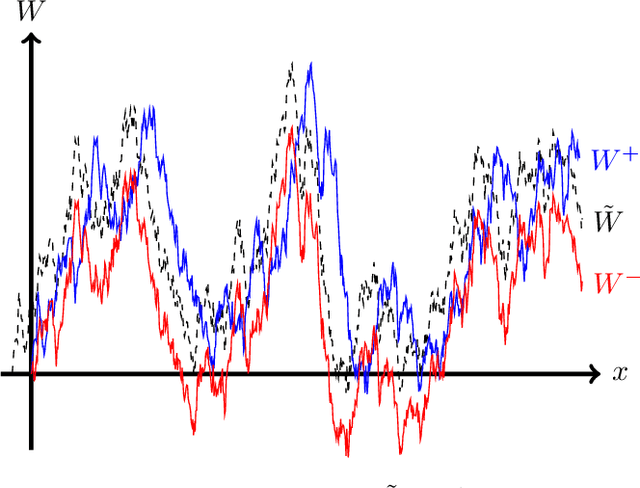
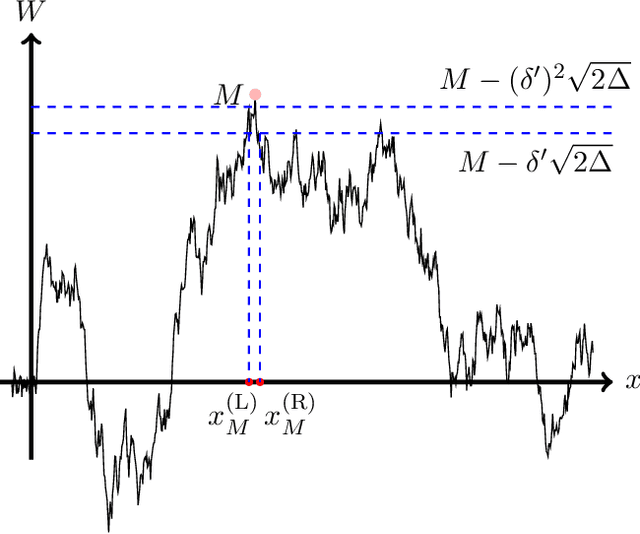
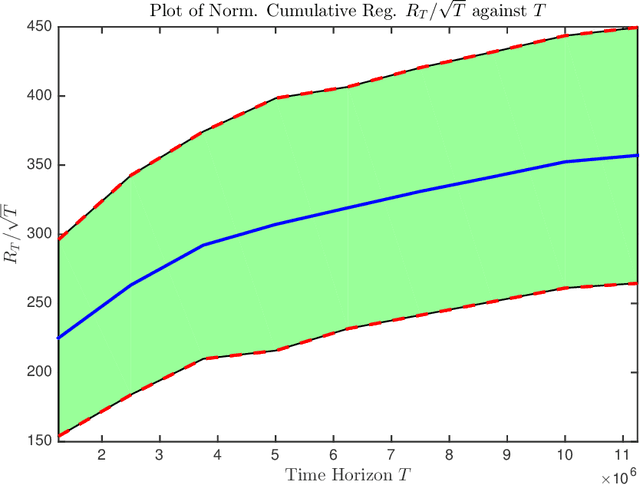
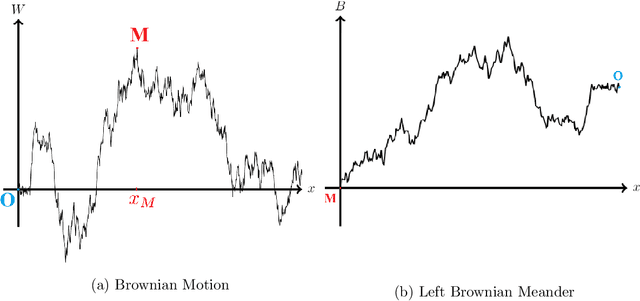
We consider the problem of Bayesian optimization of a one-dimensional Brownian motion in which the $T$ adaptively chosen observations are corrupted by Gaussian noise. We show that as the smallest possible expected simple regret and the smallest possible expected cumulative regret scale as $\Omega(1 / \sqrt{T \log (T)}) \cap \mathcal{O}(\log T / \sqrt{T})$ and $\Omega(\sqrt{T / \log (T)}) \cap \mathcal{O}(\sqrt{T} \cdot \log T)$ respectively. Thus, our upper and lower bounds are tight up to a factor of $\mathcal{O}( (\log T)^{1.5} )$. The upper bound uses an algorithm based on confidence bounds and the Markov property of Brownian motion, and the lower bound is based on a reduction to binary hypothesis testing.

Best Arm Identification for Cascading Bandits in the Fixed Confidence Setting

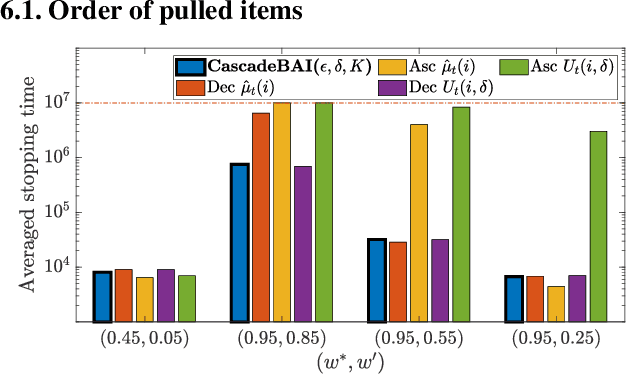
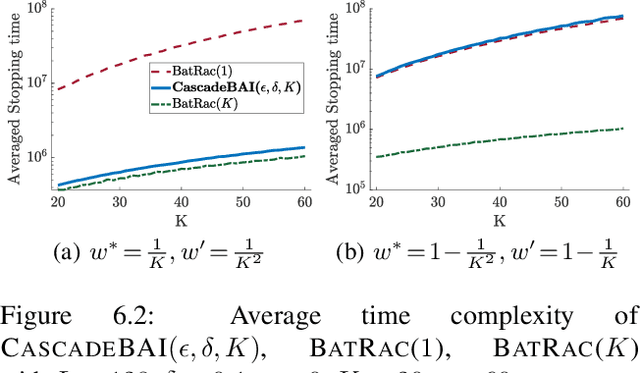
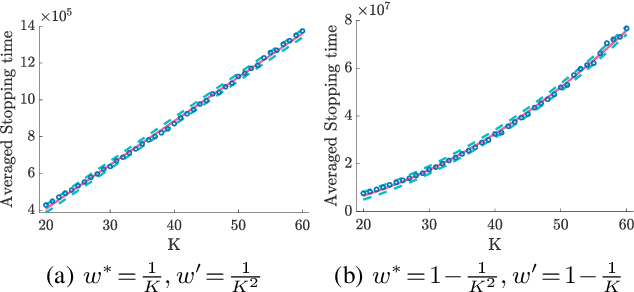
We design and analyze CascadeBAI, an algorithm for finding the best set of $K$ items, also called an arm, within the framework of cascading bandits. An upper bound on the time complexity of CascadeBAI is derived by overcoming a crucial analytical challenge, namely, that of probabilistically estimating the amount of available feedback at each step. To do so, we define a new class of random variables (r.v.'s) which we term as left-sided sub-Gaussian r.v.'s; these are r.v.'s whose cumulant generating functions (CGFs) can be bounded by a quadratic only for non-positive arguments of the CGFs. This enables the application of a sufficiently tight Bernstein-type concentration inequality. We show, through the derivation of a lower bound on the time complexity, that the performance of CascadeBAI is optimal in some practical regimes. Finally, extensive numerical simulations corroborate the efficacy of CascadeBAI as well as the tightness of our upper bound on its time complexity.

Economy Statistical Recurrent Units For Inferring Nonlinear Granger Causality

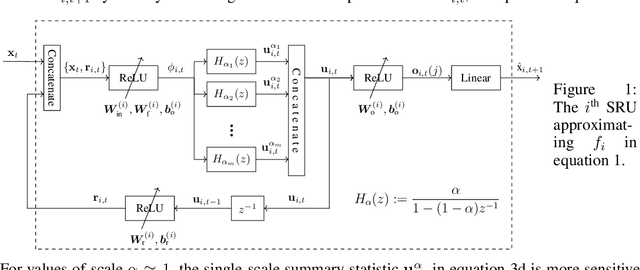
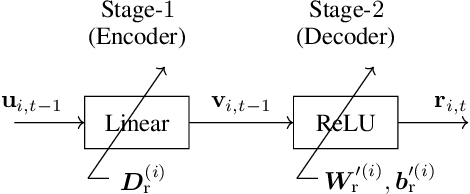
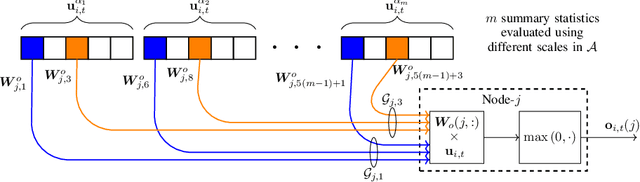
Granger causality is a widely-used criterion for analyzing interactions in large-scale networks. As most physical interactions are inherently nonlinear, we consider the problem of inferring the existence of pairwise Granger causality between nonlinearly interacting stochastic processes from their time series measurements. Our proposed approach relies on modeling the embedded nonlinearities in the measurements using a component-wise time series prediction model based on Statistical Recurrent Units (SRUs). We make a case that the network topology of Granger causal relations is directly inferrable from a structured sparse estimate of the internal parameters of the SRU networks trained to predict the processes$'$ time series measurements. We propose a variant of SRU, called economy-SRU, which, by design has considerably fewer trainable parameters, and therefore less prone to overfitting. The economy-SRU computes a low-dimensional sketch of its high-dimensional hidden state in the form of random projections to generate the feedback for its recurrent processing. Additionally, the internal weight parameters of the economy-SRU are strategically regularized in a group-wise manner to facilitate the proposed network in extracting meaningful predictive features that are highly time-localized to mimic real-world causal events. Extensive experiments are carried out to demonstrate that the proposed economy-SRU based time series prediction model outperforms the MLP, LSTM and attention-gated CNN-based time series models considered previously for inferring Granger causality.

Community Detection and Matrix Completion with Two-Sided Graph Side-Information

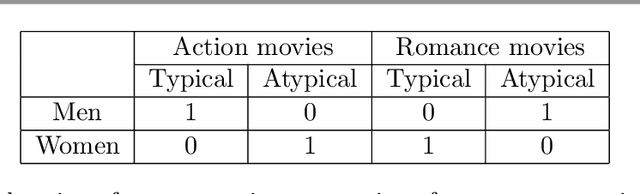
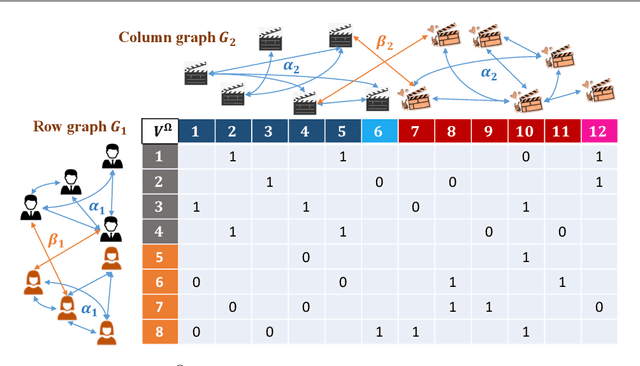
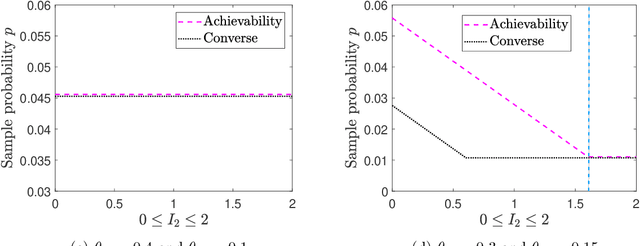
We consider the problem of recovering communities of users and communities of items (such as movies) based on a partially observed rating matrix as well as side-information in the form of similarity graphs of the users and items. The user-to-user and item-to-item similarity graphs are generated according to the celebrated stochastic block model (SBM). We develop lower and upper bounds on the minimum expected number of observed ratings (also known as the sample complexity) needed for this recovery task. These bounds are functions of various parameters including the quality of the graph side-information which is manifested in the intra- and inter-cluster probabilities of the SBMs. We show that these bounds match for a wide range of parameters of interest, and match up to a constant factor of two for the remaining parameter regime. Our information-theoretic results quantify the benefits of the two-sided graph side-information for recovery, and further analysis reveals that the two pieces of graph side-information produce an interesting synergistic effect under certain scenarios. This means that if one observes only one of the two graphs, then the required sample complexity worsens to the case in which none of the graphs is observed. Thus both graphs are strictly needed to reduce the sample complexity.

Sequential Classification with Empirically Observed Statistics

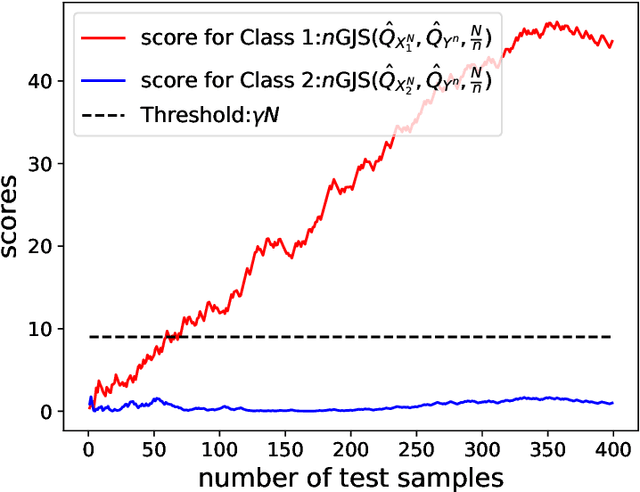
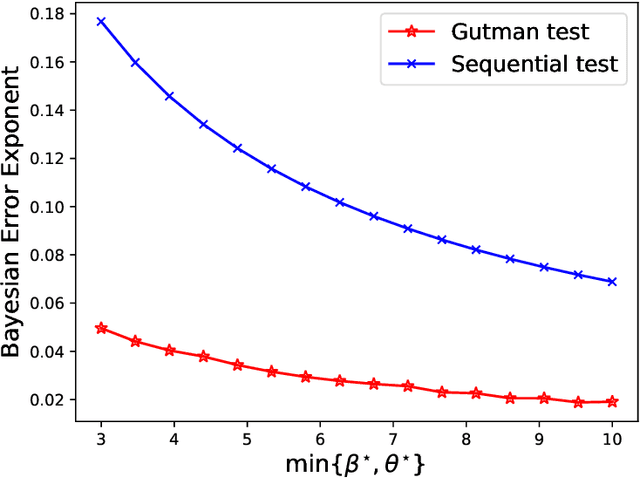
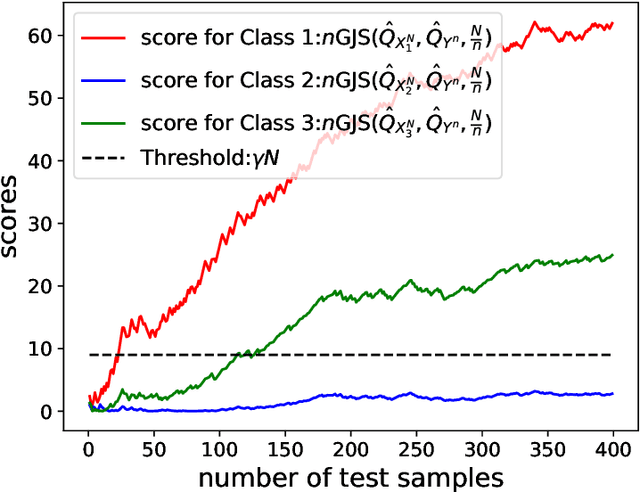
Motivated by real-world machine learning applications, we consider a statistical classification task in a sequential setting where test samples arrive sequentially. In addition, the generating distributions are unknown and only a set of empirically sampled sequences are available to a decision maker. The decision maker is tasked to classify a test sequence which is known to be generated according to either one of the distributions. In particular, for the binary case, the decision maker wishes to perform the classification task with minimum number of the test samples, so, at each step, she declares that either hypothesis 1 is true, hypothesis 2 is true, or she requests for an additional test sample. We propose a classifier and analyze the type-I and type-II error probabilities. We demonstrate the significant advantage of our sequential scheme compared to an existing non-sequential classifier proposed by Gutman. Finally, we extend our setup and results to the multi-class classification scenario and again demonstrate that the variable-length nature of the problem affords significant advantages as one can achieve the same set of exponents as Gutman's fixed-length setting but without having the rejection option.

On Robustness of Neural Ordinary Differential Equations

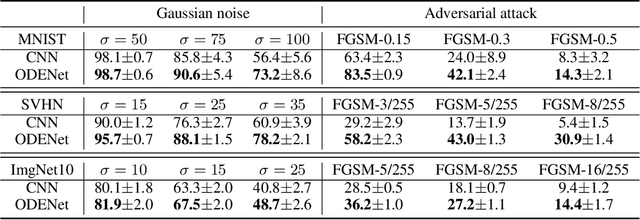
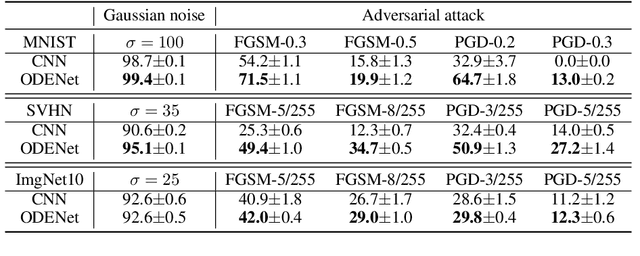
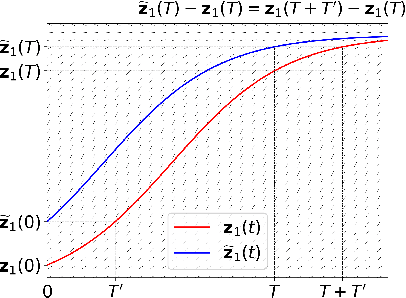
Neural ordinary differential equations (ODEs) have been attracting increasing attention in various research domains recently. There have been some works studying optimization issues and approximation capabilities of neural ODEs, but their robustness is still yet unclear. In this work, we fill this important gap by exploring robustness properties of neural ODEs both empirically and theoretically. We first present an empirical study on the robustness of the neural ODE-based networks (ODENets) by exposing them to inputs with various types of perturbations and subsequently investigating the changes of the corresponding outputs. In contrast to conventional convolutional neural networks (CNNs), we find that the ODENets are more robust against both random Gaussian perturbations and adversarial attack examples. We then provide an insightful understanding of this phenomenon by exploiting a certain desirable property of the flow of a continuous-time ODE, namely that integral curves are non-intersecting. Our work suggests that, due to their intrinsic robustness, it is promising to use neural ODEs as a basic block for building robust deep network models. To further enhance the robustness of vanilla neural ODEs, we propose the time-invariant steady neural ODE (TisODE), which regularizes the flow on perturbed data via the time-invariant property and the imposition of a steady-state constraint. We show that the TisODE method outperforms vanilla neural ODEs and also can work in conjunction with other state-of-the-art architectural methods to build more robust deep networks.