A Unifying Theory of Thompson Sampling for Continuous Risk-Averse Bandits

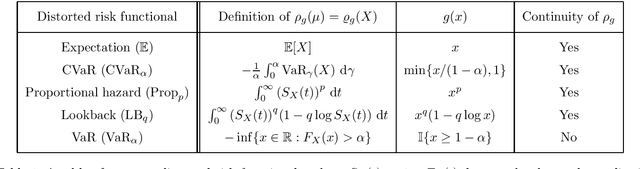
This paper unifies the design and simplifies the analysis of risk-averse Thompson sampling algorithms for the multi-armed bandit problem for a generic class of risk functionals \r{ho} that are continuous. Using the contraction principle in the theory of large deviations, we prove novel concentration bounds for these continuous risk functionals. In contrast to existing works in which the bounds depend on the samples themselves, our bounds only depend on the number of samples. This allows us to sidestep significant analytical challenges and unify existing proofs of the regret bounds of existing Thompson sampling-based algorithms. We show that a wide class of risk functionals as well as "nice" functions of them satisfy the continuity condition. Using our newly developed analytical toolkits, we analyse the algorithms $\rho$-MTS (for multinomial distributions) and $\rho$-NPTS (for bounded distributions) and prove that they admit asymptotically optimal regret bounds of risk-averse algorithms under the mean-variance, CVaR, and other ubiquitous risk measures, as well as a host of newly synthesized risk measures. Numerical simulations show that our bounds are reasonably tight vis-\`a-vis algorithm-independent lower bounds.

Robustifying Algorithms of Learning Latent Trees with Vector Variables

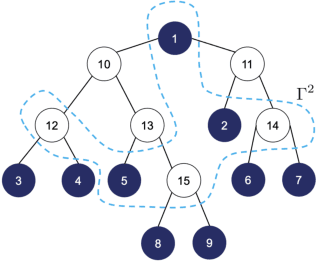
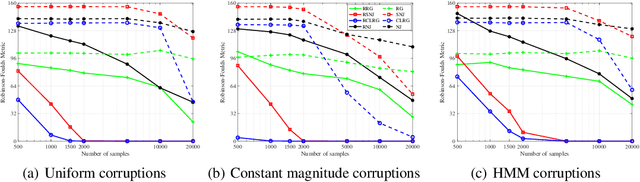
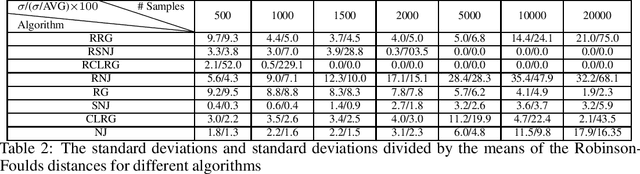
We consider learning the structures of Gaussian latent tree models with vector observations when a subset of them are arbitrarily corrupted. First, we present the sample complexities of Recursive Grouping (RG) and Chow-Liu Recursive Grouping (CLRG) without the assumption that the effective depth is bounded in the number of observed nodes, significantly generalizing the results in Choi et al. (2011). We show that Chow-Liu initialization in CLRG greatly reduces the sample complexity of RG from being exponential in the diameter of the tree to only logarithmic in the diameter for the hidden Markov model (HMM). Second, we robustify RG, CLRG, Neighbor Joining (NJ) and Spectral NJ (SNJ) by using the truncated inner product. These robustified algorithms can tolerate a number of corruptions up to the square root of the number of clean samples. Finally, we derive the first known instance-dependent impossibility result for structure learning of latent trees. The optimalities of the robust version of CLRG and NJ are verified by comparing their sample complexities and the impossibility result.

Towards Minimax Optimal Best Arm Identification in Linear Bandits

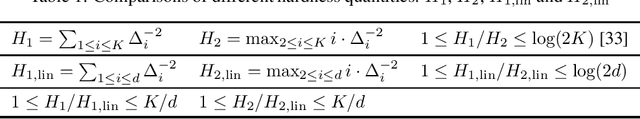
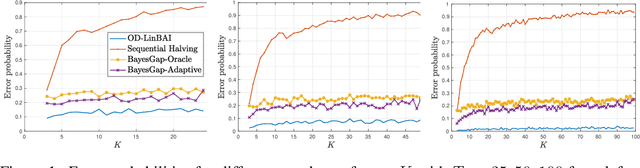
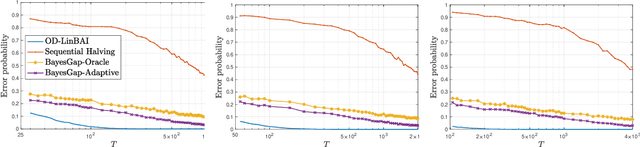
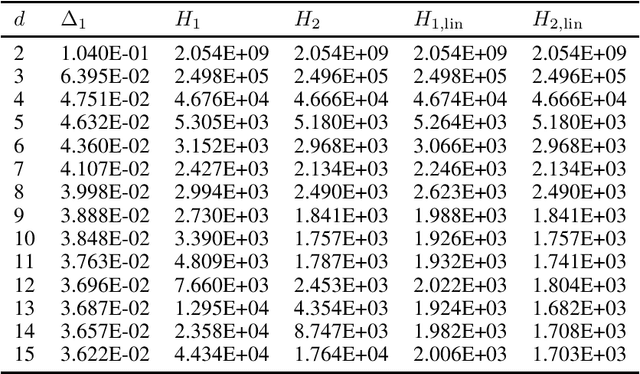
We study the problem of best arm identification in linear bandits in the fixed-budget setting. By leveraging properties of the G-optimal design and incorporating it into the arm allocation rule, we design a parameter-free algorithm, Optimal Design-based Linear Best Arm Identification (OD-LinBAI). We provide a theoretical analysis of the failure probability of OD-LinBAI. While the performances of existing methods (e.g., BayesGap) depend on all the optimality gaps, OD-LinBAI depends on the gaps of the top $d$ arms, where $d$ is the effective dimension of the linear bandit instance. Furthermore, we present a minimax lower bound for this problem. The upper and lower bounds show that OD-LinBAI is minimax optimal up to multiplicative factors in the exponent. Finally, numerical experiments corroborate our theoretical findings.

Exact Recovery in the General Hypergraph Stochastic Block Model

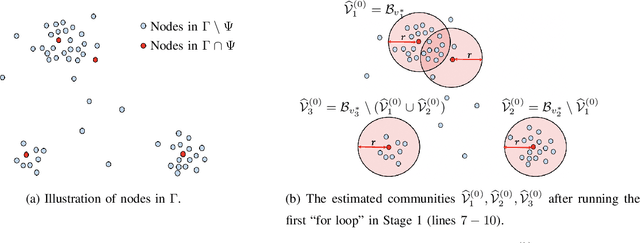
This paper investigates fundamental limits of exact recovery in the general d-uniform hypergraph stochastic block model (d-HSBM), wherein n nodes are partitioned into k disjoint communities with relative sizes (p1,..., pk). Each subset of nodes with cardinality d is generated independently as an order-d hyperedge with a certain probability that depends on the ground-truth communities that the d nodes belong to. The goal is to exactly recover the k hidden communities based on the observed hypergraph. We show that there exists a sharp threshold such that exact recovery is achievable above the threshold and impossible below the threshold (apart from a small regime of parameters that will be specified precisely). This threshold is represented in terms of a quantity which we term as the generalized Chernoff-Hellinger divergence between communities. Our result for this general model recovers prior results for the standard SBM and d-HSBM with two symmetric communities as special cases. En route to proving our achievability results, we develop a polynomial-time two-stage algorithm that meets the threshold. The first stage adopts a certain hypergraph spectral clustering method to obtain a coarse estimate of communities, and the second stage refines each node individually via local refinement steps to ensure exact recovery.

Adversarially-Trained Nonnegative Matrix Factorization

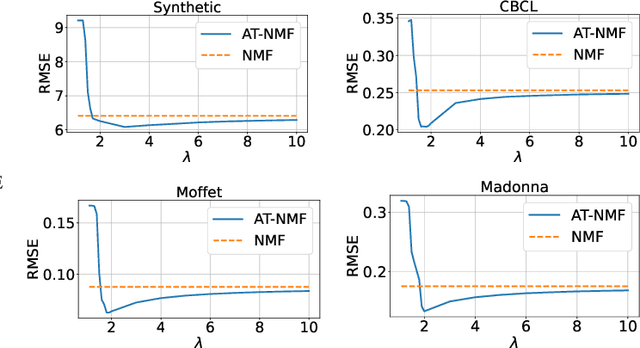
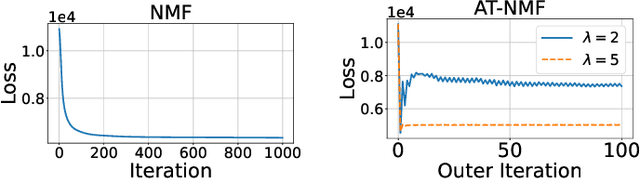
We consider an adversarially-trained version of the nonnegative matrix factorization, a popular latent dimensionality reduction technique. In our formulation, an attacker adds an arbitrary matrix of bounded norm to the given data matrix. We design efficient algorithms inspired by adversarial training to optimize for dictionary and coefficient matrices with enhanced generalization abilities. Extensive simulations on synthetic and benchmark datasets demonstrate the superior predictive performance on matrix completion tasks of our proposed method compared to state-of-the-art competitors, including other variants of adversarial nonnegative matrix factorization.

CIFS: Improving Adversarial Robustness of CNNs via Channel-wise Importance-based Feature Selection

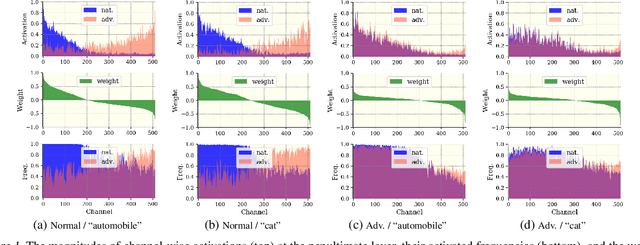
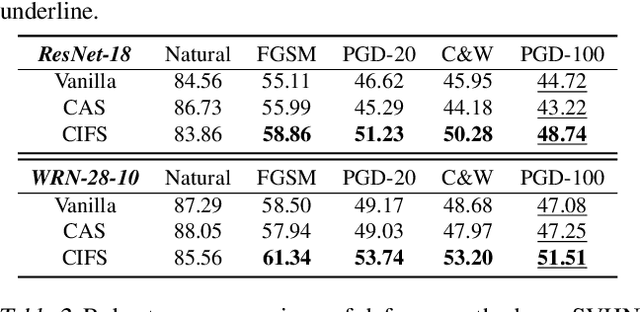
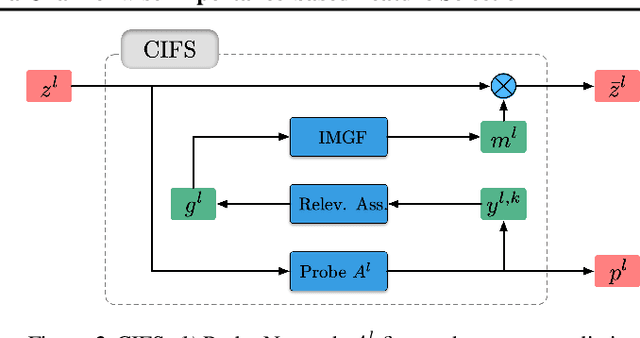
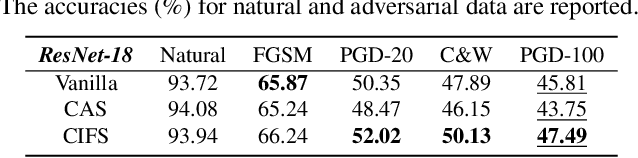
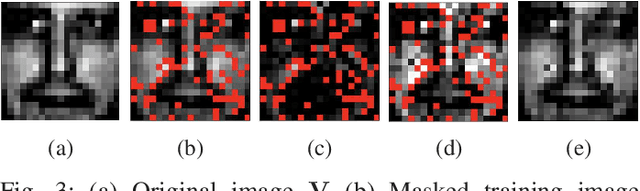
We investigate the adversarial robustness of CNNs from the perspective of channel-wise activations. By comparing \textit{non-robust} (normally trained) and \textit{robustified} (adversarially trained) models, we observe that adversarial training (AT) robustifies CNNs by aligning the channel-wise activations of adversarial data with those of their natural counterparts. However, the channels that are \textit{negatively-relevant} (NR) to predictions are still over-activated when processing adversarial data. Besides, we also observe that AT does not result in similar robustness for all classes. For the robust classes, channels with larger activation magnitudes are usually more \textit{positively-relevant} (PR) to predictions, but this alignment does not hold for the non-robust classes. Given these observations, we hypothesize that suppressing NR channels and aligning PR ones with their relevances further enhances the robustness of CNNs under AT. To examine this hypothesis, we introduce a novel mechanism, i.e., \underline{C}hannel-wise \underline{I}mportance-based \underline{F}eature \underline{S}election (CIFS). The CIFS manipulates channels' activations of certain layers by generating non-negative multipliers to these channels based on their relevances to predictions. Extensive experiments on benchmark datasets including CIFAR10 and SVHN clearly verify the hypothesis and CIFS's effectiveness of robustifying CNNs.

SGA: A Robust Algorithm for Partial Recovery of Tree-Structured Graphical Models with Noisy Samples

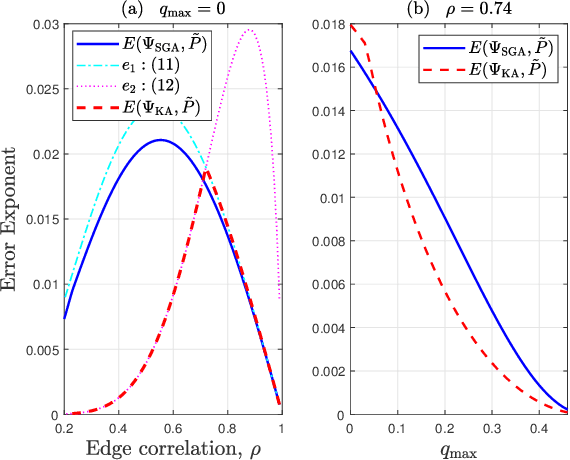
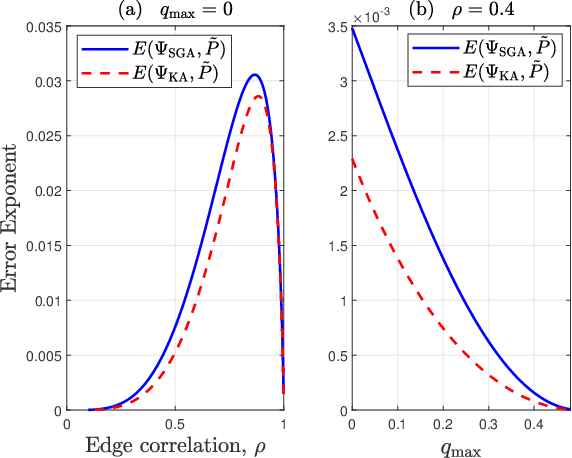
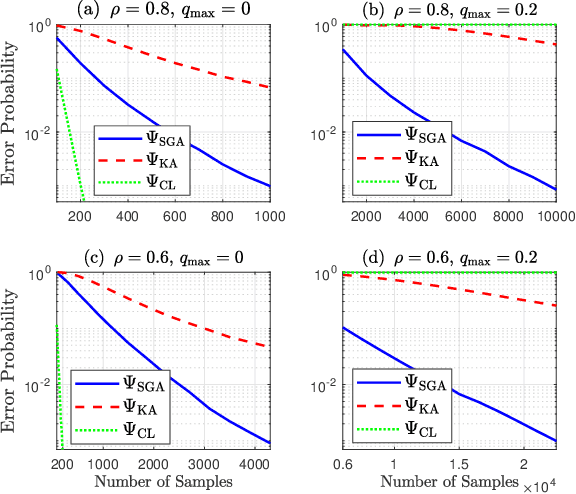
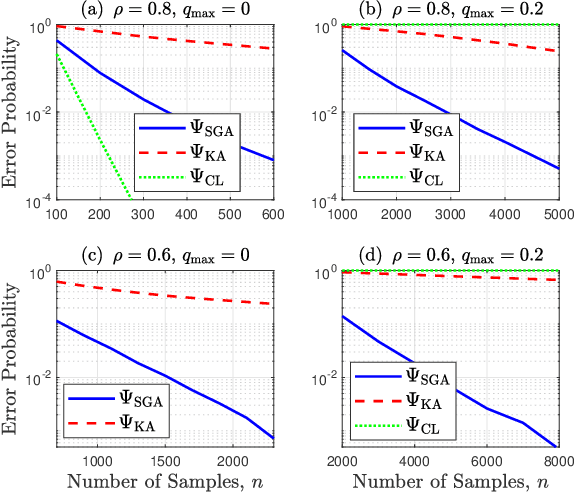
We consider learning Ising tree models when the observations from the nodes are corrupted by independent but non-identically distributed noise with unknown statistics. Katiyar et al. (2020) showed that although the exact tree structure cannot be recovered, one can recover a partial tree structure; that is, a structure belonging to the equivalence class containing the true tree. This paper presents a systematic improvement of Katiyar et al. (2020). First, we present a novel impossibility result by deriving a bound on the necessary number of samples for partial recovery. Second, we derive a significantly improved sample complexity result in which the dependence on the minimum correlation $\rho_{\min}$ is $\rho_{\min}^{-8}$ instead of $\rho_{\min}^{-24}$. Finally, we propose Symmetrized Geometric Averaging (SGA), a more statistically robust algorithm for partial tree recovery. We provide error exponent analyses and extensive numerical results on a variety of trees to show that the sample complexity of SGA is significantly better than the algorithm of Katiyar et al. (2020). SGA can be readily extended to Gaussian models and is shown via numerical experiments to be similarly superior.

Risk-Constrained Thompson Sampling for CVaR Bandits

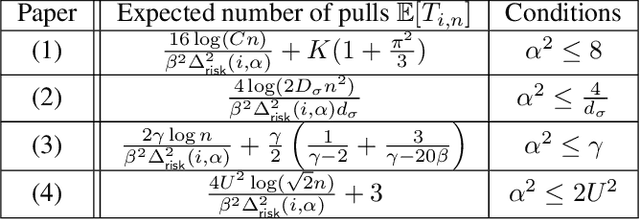
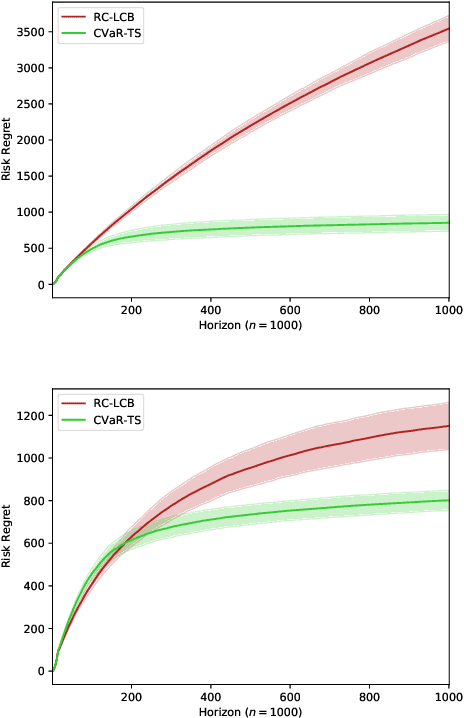
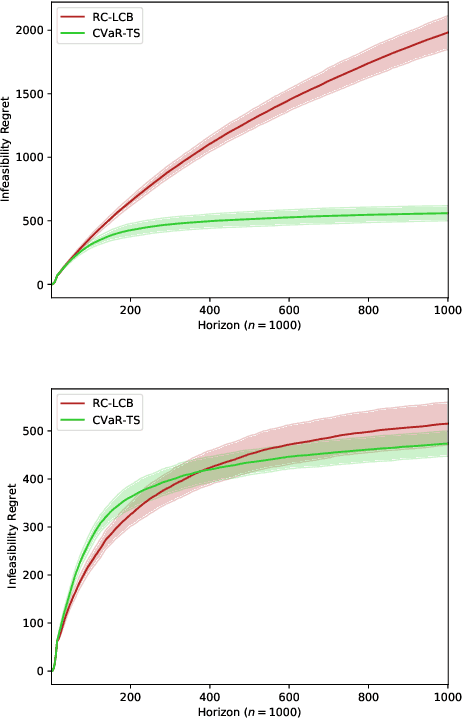
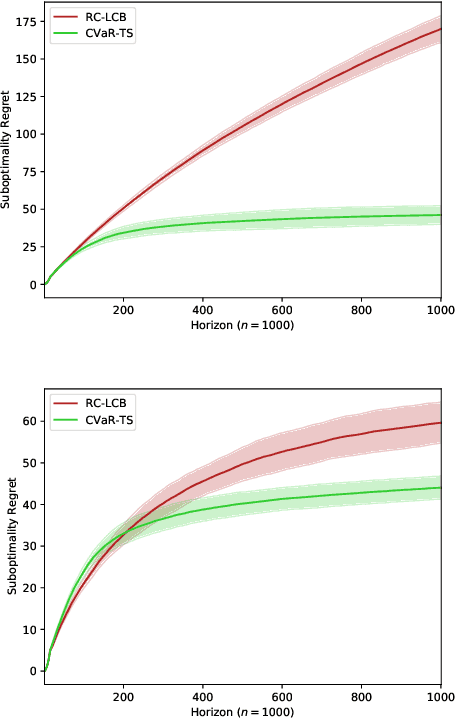
The multi-armed bandit (MAB) problem is a ubiquitous decision-making problem that exemplifies the exploration-exploitation tradeoff. Standard formulations exclude risk in decision making. Risk notably complicates the basic reward-maximising objective, in part because there is no universally agreed definition of it. In this paper, we consider a popular risk measure in quantitative finance known as the Conditional Value at Risk (CVaR). We explore the performance of a Thompson Sampling-based algorithm CVaR-TS under this risk measure. We provide comprehensive comparisons between our regret bounds with state-of-the-art L/UCB-based algorithms in comparable settings and demonstrate their clear improvement in performance. We also include numerical simulations to empirically verify that CVaR-TS outperforms other L/UCB-based algorithms.

Probabilistic Sequential Shrinking: A Best Arm Identification Algorithm for Stochastic Bandits with Corruptions

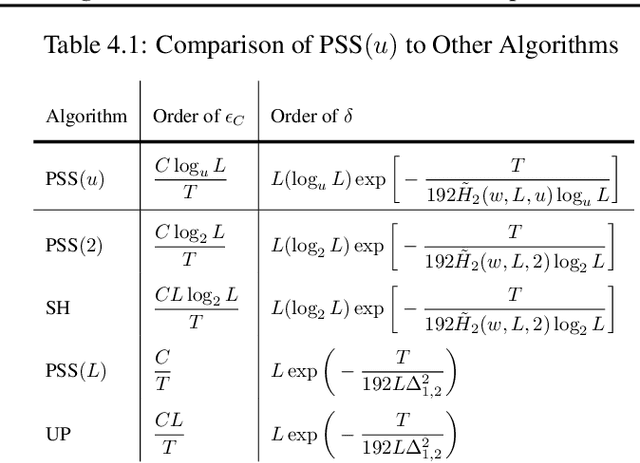
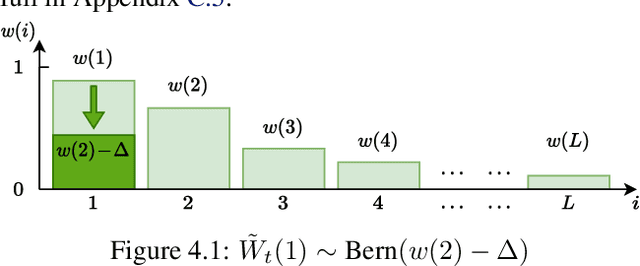
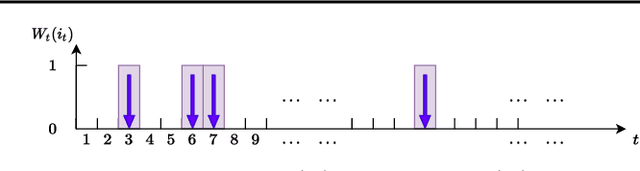
We consider a best arm identification (BAI) problem for stochastic bandits with adversarial corruptions in the fixed-budget setting of $T$ steps. We design a novel randomized algorithm, Probabilistic Sequential Shrinking$(u)$ (PSS$(u)$), which is agnostic to the amount of corruptions. When the amount of corruptions per step (CPS) is below a threshold, PSS$(u)$ identifies the best arm or item with probability tending to $1$ as $T\rightarrow\infty$. Otherwise, the optimality gap of the identified item degrades gracefully with the CPS. We argue that such a bifurcation is necessary. In addition, we show that when the CPS is sufficiently large, no algorithm can achieve a BAI probability tending to $1$ as $T\rightarrow \infty$. In PSS$(u)$, the parameter $u$ serves to balance between the optimality gap and success probability. En route, the injection of randomization is shown to be essential to mitigate the impact of corruptions. Indeed, we show that PSS$(u)$ has a better performance than its deterministic analogue, the Successive Halving (SH) algorithm by Karnin et al. (2013). PSS$(2)$'s performance guarantee matches SH's when there is no corruption. Finally, we identify a term in the exponent of the failure probability of PSS$(u)$ that generalizes the common $H_2$ term for BAI under the fixed-budget setting.

Positive Semidefinite Matrix Factorization: A Connection with Phase Retrieval and Affine Rank Minimization

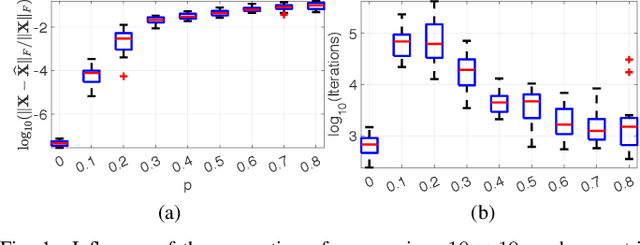
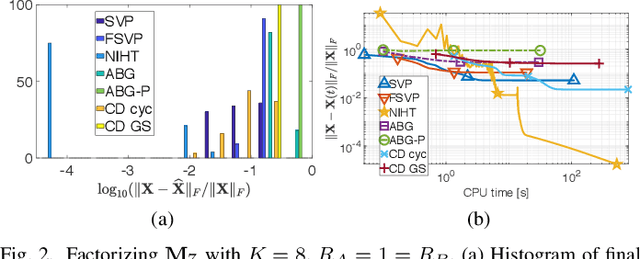
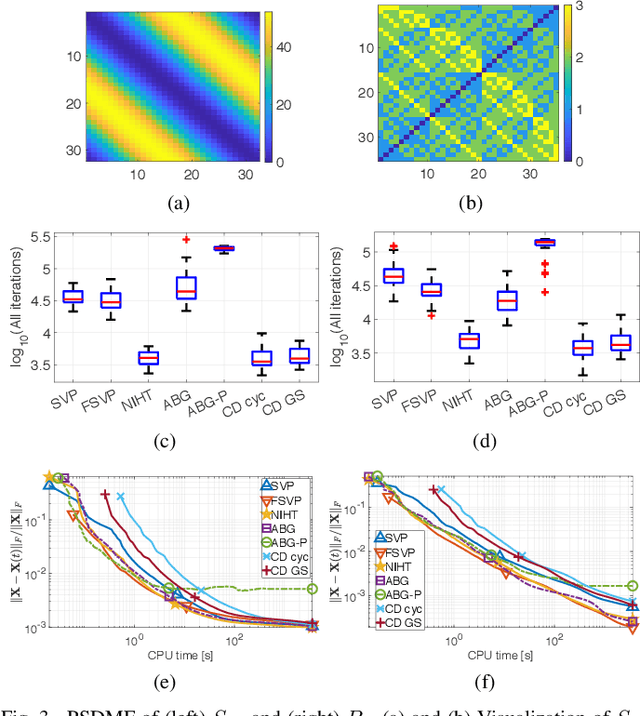
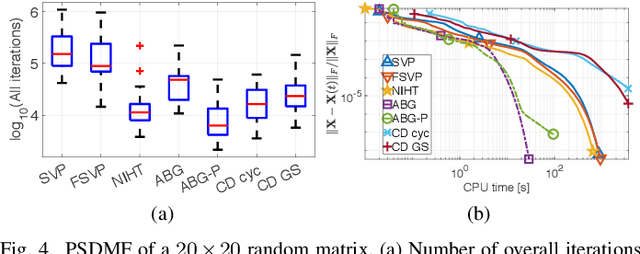
Positive semidefinite matrix factorization (PSDMF) expresses each entry of a nonnegative matrix as the inner product of two positive semidefinite (psd) matrices. When all these psd matrices are constrained to be diagonal, this model is equivalent to nonnegative matrix factorization. Applications include combinatorial optimization, quantum-based statistical models, and recommender systems, among others. However, despite the increasing interest in PSDMF, only a few PSDMF algorithms were proposed in the literature. In this paper, we show that PSDMF algorithms can be designed based on phase retrieval (PR) and affine rank minimization (ARM) algorithms. This procedure allows a significant shortcut in designing new PSDMF algorithms, as it allows to leverage some of the useful numerical properties of existing PR and ARM methods to the PSDMF framework. Motivated by this idea, we introduce a new family of PSDMF algorithms based on singular value projection (SVP) and iterative hard thresholding (IHT). This family subsumes previously-proposed projected gradient PSDMF methods; additionally, we show a new connection between SVP-based methods and majorization-minimization. Numerical experiments show that our proposed methods outperform state-of-the-art coordinate descent algorithms in terms of convergence speed and computational complexity, in certain scenarios. In certain cases, our proposed normalized-IHT-based method is the only algorithm able to find a solution. These results support our claim that the PSDMF framework can inherit desired numerical properties from PR and ARM algorithms, leading to more efficient PSDMF algorithms, and motivate further study of the links between these models.