Semiparametric Contextual Bandits

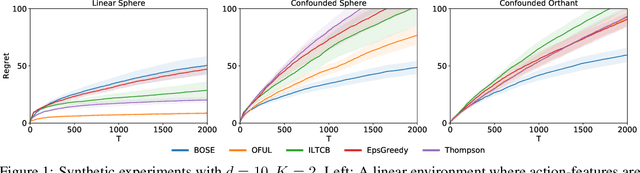
This paper studies semiparametric contextual bandits, a generalization of the linear stochastic bandit problem where the reward for an action is modeled as a linear function of known action features confounded by an non-linear action-independent term. We design new algorithms that achieve $\tilde{O}(d\sqrt{T})$ regret over $T$ rounds, when the linear function is $d$-dimensional, which matches the best known bounds for the simpler unconfounded case and improves on a recent result of Greenewald et al. (2017). Via an empirical evaluation, we show that our algorithms outperform prior approaches when there are non-linear confounding effects on the rewards. Technically, our algorithms use a new reward estimator inspired by doubly-robust approaches and our proofs require new concentration inequalities for self-normalized martingales.

Orthogonal Random Forest for Heterogeneous Treatment Effect Estimation

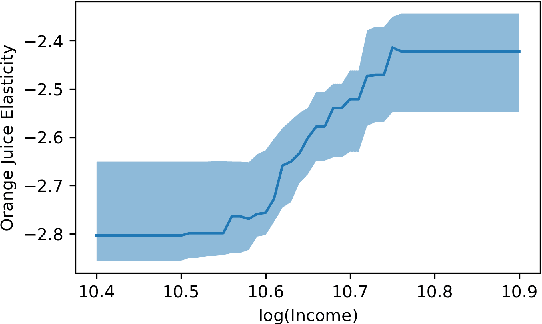
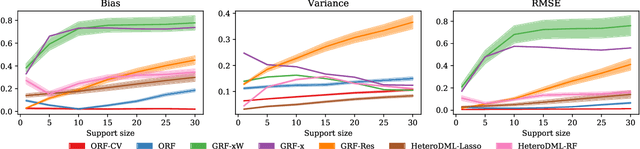
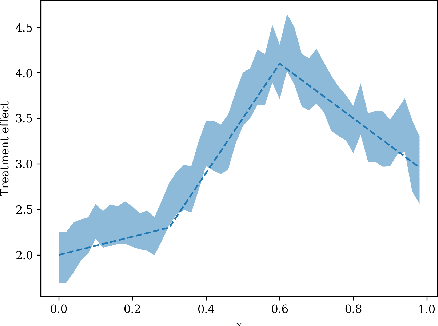
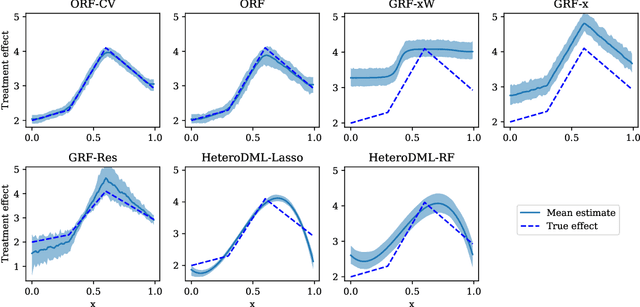
We study the problem of estimating heterogeneous treatment effects from observational data, where the treatment policy on the collected data was determined by potentially many confounding observable variables. We propose orthogonal random forest, an algorithm that combines orthogonalization, a technique that effectively removes the confounding effect in two-stage estimation, with generalized random forests [Athey et al., 2017], a flexible method for estimating treatment effect heterogeneity. We prove a consistency rate result of our estimator in the partially linear regression model, and en route we provide a consistency analysis for a general framework of performing generalized method of moments (GMM) estimation. We also provide a comprehensive empirical evaluation of our algorithms, and show that they consistently outperform baseline approaches.

Bayesian Exploration: Incentivizing Exploration in Bayesian Games

We consider a ubiquitous scenario in the Internet economy when individual decision-makers (henceforth, agents) both produce and consume information as they make strategic choices in an uncertain environment. This creates a three-way tradeoff between exploration (trying out insufficiently explored alternatives to help others in the future), exploitation (making optimal decisions given the information discovered by other agents), and incentives of the agents (who are myopically interested in exploitation, while preferring the others to explore). We posit a principal who controls the flow of information from agents that came before, and strives to coordinate the agents towards a socially optimal balance between exploration and exploitation, not using any monetary transfers. The goal is to design a recommendation policy for the principal which respects agents' incentives and minimizes a suitable notion of regret. We extend prior work in this direction to allow the agents to interact with one another in a shared environment: at each time step, multiple agents arrive to play a Bayesian game, receive recommendations, choose their actions, receive their payoffs, and then leave the game forever. The agents now face two sources of uncertainty: the actions of the other agents and the parameters of the uncertain game environment. Our main contribution is to show that the principal can achieve constant regret when the utilities are deterministic (where the constant depends on the prior distribution, but not on the time horizon), and logarithmic regret when the utilities are stochastic. As a key technical tool, we introduce the concept of explorable actions, the actions which some incentive-compatible policy can recommend with non-zero probability. We show how the principal can identify (and explore) all explorable actions, and use the revealed information to perform optimally.

Plug-in Regularized Estimation of High-Dimensional Parameters in Nonlinear Semiparametric Models

We develop a theory for estimation of a high-dimensional sparse parameter $\theta$ defined as a minimizer of a population loss function $L_D(\theta,g_0)$ which, in addition to $\theta$, depends on a, potentially infinite dimensional, nuisance parameter $g_0$. Our approach is based on estimating $\theta$ via an $\ell_1$-regularized minimization of a sample analog of $L_S(\theta, \hat{g})$, plugging in a first-stage estimate $\hat{g}$, computed on a hold-out sample. We define a population loss to be (Neyman) orthogonal if the gradient of the loss with respect to $\theta$, has pathwise derivative with respect to $g$ equal to zero, when evaluated at the true parameter and nuisance component. We show that orthogonality implies a second-order impact of the first stage nuisance error on the second stage target parameter estimate. Our approach applies to both convex and non-convex losses, albeit the latter case requires a small adaptation of our method with a preliminary estimation step of the target parameter. Our result enables oracle convergence rates for $\theta$ under assumptions on the first stage rates, typically of the order of $n^{-1/4}$. We show how such an orthogonal loss can be constructed via a novel orthogonalization process for a general model defined by conditional moment restrictions. We apply our theory to high-dimensional versions of standard estimation problems in statistics and econometrics, such as: estimation of conditional moment models with missing data, estimation of structural utilities in games of incomplete information and estimation of treatment effects in regression models with non-linear link functions.

Accurate Inference for Adaptive Linear Models

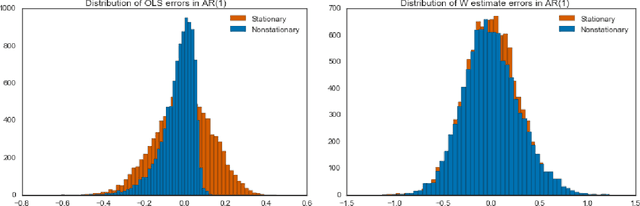
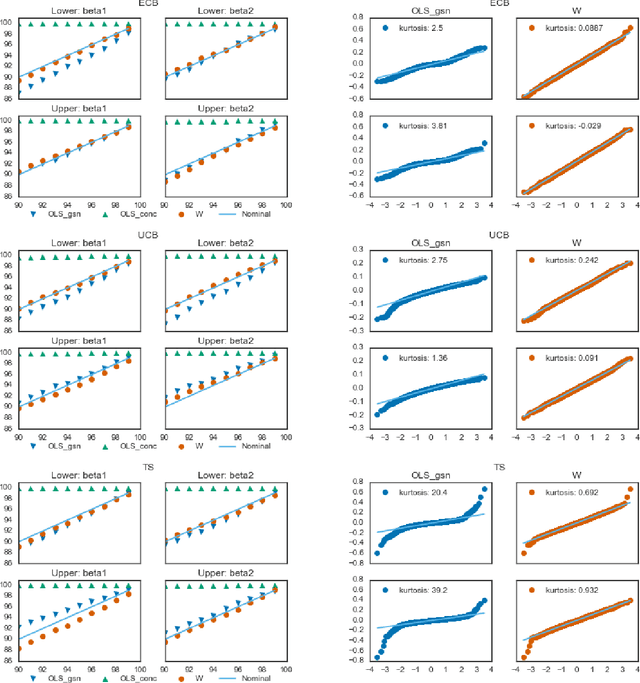
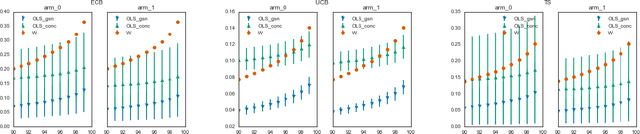
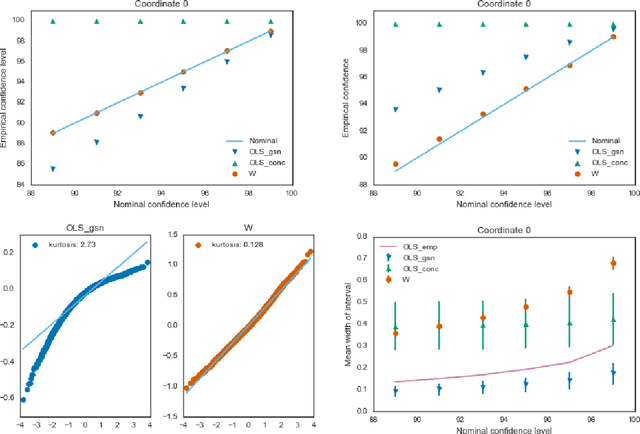
Estimators computed from adaptively collected data do not behave like their non-adaptive brethren. Rather, the sequential dependence of the collection policy can lead to severe distributional biases that persist even in the infinite data limit. We develop a general method -- $\mathbf{W}$-decorrelation -- for transforming the bias of adaptive linear regression estimators into variance. The method uses only coarse-grained information about the data collection policy and does not need access to propensity scores or exact knowledge of the policy. We bound the finite-sample bias and variance of the $\mathbf{W}$-estimator and develop asymptotically correct confidence intervals based on a novel martingale central limit theorem. We then demonstrate the empirical benefits of the generic $\mathbf{W}$-decorrelation procedure in two different adaptive data settings: the multi-armed bandit and the autoregressive time series.

Learning to Bid Without Knowing your Value

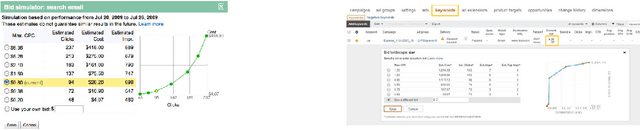
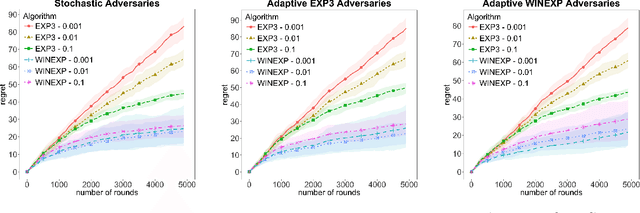
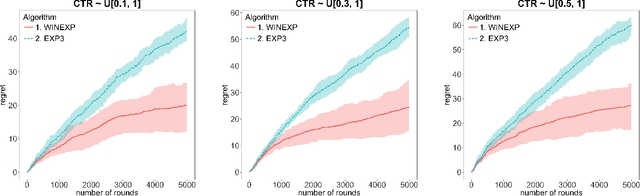
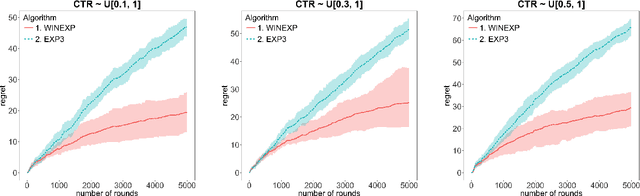
We address online learning in complex auction settings, such as sponsored search auctions, where the value of the bidder is unknown to her, evolving in an arbitrary manner and observed only if the bidder wins an allocation. We leverage the structure of the utility of the bidder and the partial feedback that bidders typically receive in auctions, in order to provide algorithms with regret rates against the best fixed bid in hindsight, that are exponentially faster in convergence in terms of dependence on the action space, than what would have been derived by applying a generic bandit algorithm and almost equivalent to what would have been achieved in the full information setting. Our results are enabled by analyzing a new online learning setting with outcome-based feedback, which generalizes learning with feedback graphs. We provide an online learning algorithm for this setting, of independent interest, with regret that grows only logarithmically with the number of actions and linearly only in the number of potential outcomes (the latter being very small in most auction settings). Last but not least, we show that our algorithm outperforms the bandit approach experimentally and that this performance is robust to dropping some of our theoretical assumptions or introducing noise in the feedback that the bidder receives.

Optimal and Myopic Information Acquisition

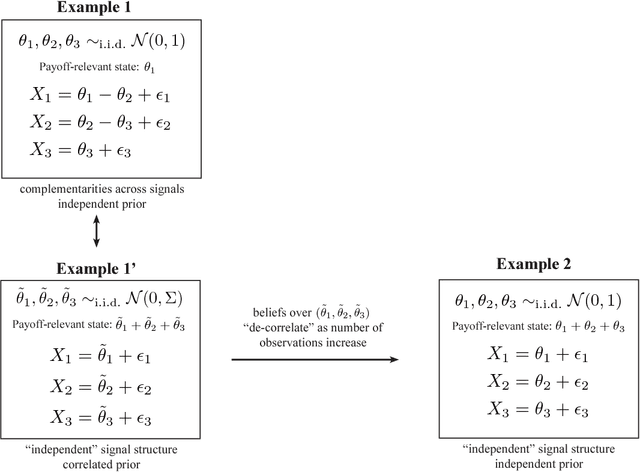
We consider the problem of optimal dynamic information acquisition from many correlated information sources. Each period, the decision-maker jointly takes an action and allocates a fixed number of observations across the available sources. His payoff depends on the actions taken and on an unknown state. In the canonical setting of jointly normal information sources, we show that the optimal dynamic information acquisition rule proceeds myopically after finitely many periods. If signals are acquired in large blocks each period, then the optimal rule turns out to be myopic from period 1. These results demonstrate the possibility of robust and "simple" optimal information acquisition, and simplify the analysis of dynamic information acquisition in a widely used informational environment.

Adversarial Generalized Method of Moments

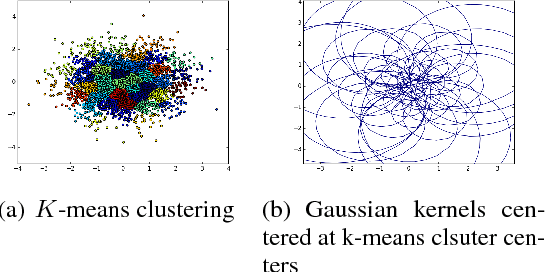
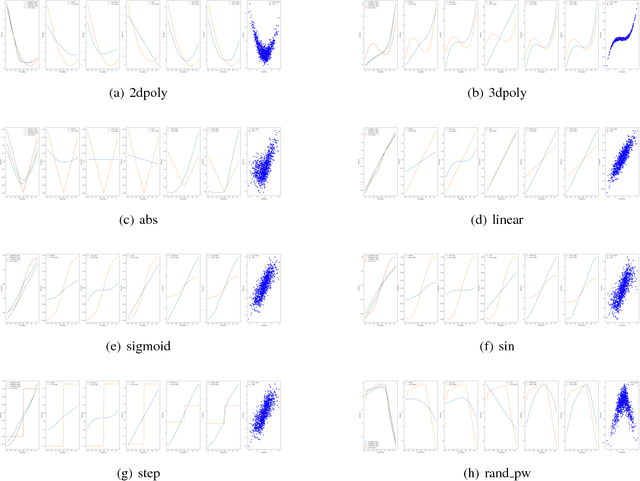
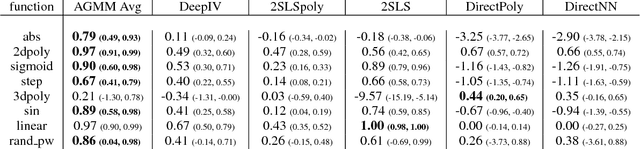
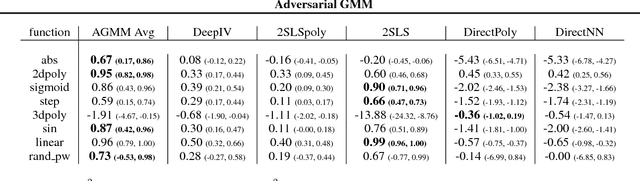
We provide an approach for learning deep neural net representations of models described via conditional moment restrictions. Conditional moment restrictions are widely used, as they are the language by which social scientists describe the assumptions they make to enable causal inference. We formulate the problem of estimating the underling model as a zero-sum game between a modeler and an adversary and apply adversarial training. Our approach is similar in nature to Generative Adversarial Networks (GAN), though here the modeler is learning a representation of a function that satisfies a continuum of moment conditions and the adversary is identifying violating moments. We outline ways of constructing effective adversaries in practice, including kernels centered by k-means clustering, and random forests. We examine the practical performance of our approach in the setting of non-parametric instrumental variable regression.

Inference on Auctions with Weak Assumptions on Information

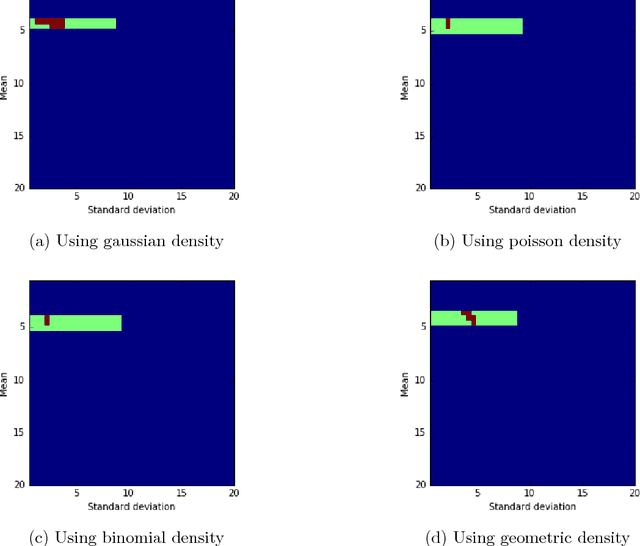
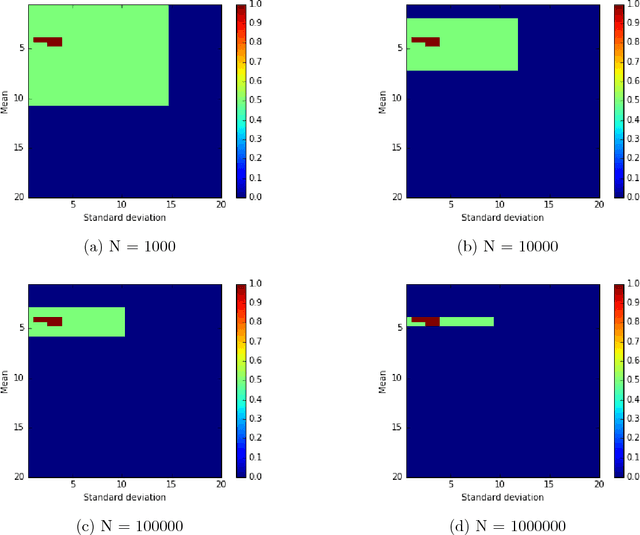
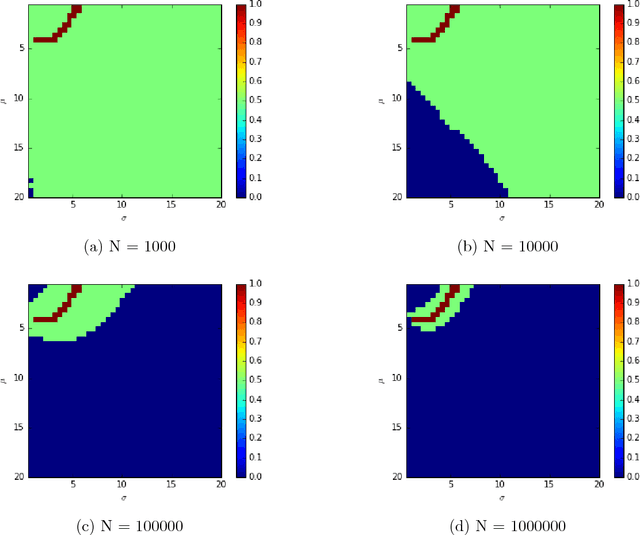
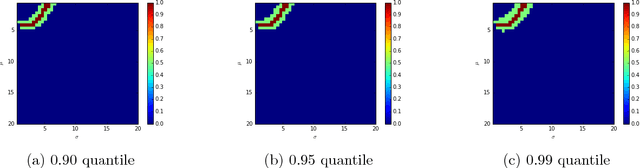
Given a sample of bids from independent auctions, this paper examines the question of inference on auction fundamentals (e.g. valuation distributions, welfare measures) under weak assumptions on information structure. The question is important as it allows us to learn about the valuation distribution in a robust way, i.e., without assuming that a particular information structure holds across observations. We leverage the recent contributions of \cite{Bergemann2013} in the robust mechanism design literature that exploit the link between Bayesian Correlated Equilibria and Bayesian Nash Equilibria in incomplete information games to construct an econometrics framework for learning about auction fundamentals using observed data on bids. We showcase our construction of identified sets in private value and common value auctions. Our approach for constructing these sets inherits the computational simplicity of solving for correlated equilibria: checking whether a particular valuation distribution belongs to the identified set is as simple as determining whether a {\it linear} program is feasible. A similar linear program can be used to construct the identified set on various welfare measures and counterfactual objects. For inference and to summarize statistical uncertainty, we propose novel finite sample methods using tail inequalities that are used to construct confidence regions on sets. We also highlight methods based on Bayesian bootstrap and subsampling. A set of Monte Carlo experiments show adequate finite sample properties of our inference procedures. We illustrate our methods using data from OCS auctions.

Expert identification of visual primitives used by CNNs during mammogram classification

This work interprets the internal representations of deep neural networks trained for classification of diseased tissue in 2D mammograms. We propose an expert-in-the-loop interpretation method to label the behavior of internal units in convolutional neural networks (CNNs). Expert radiologists identify that the visual patterns detected by the units are correlated with meaningful medical phenomena such as mass tissue and calcificated vessels. We demonstrate that several trained CNN models are able to produce explanatory descriptions to support the final classification decisions. We view this as an important first step toward interpreting the internal representations of medical classification CNNs and explaining their predictions.