Vasilis Syrgkanis
Towards efficient representation identification in supervised learning
Apr 10, 2022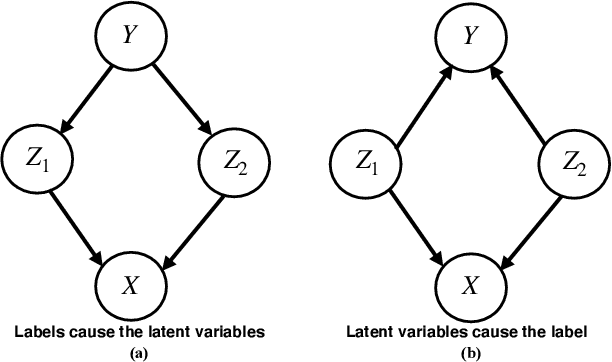
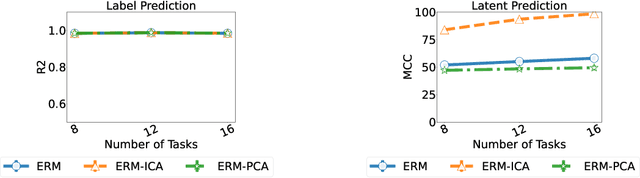
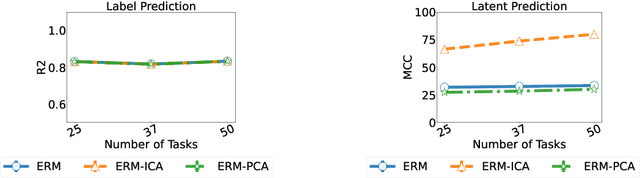
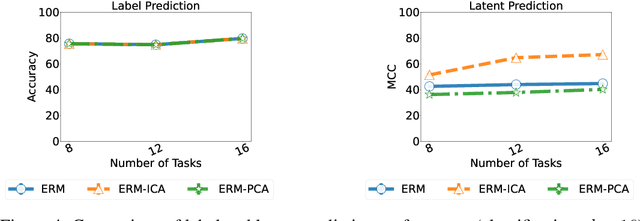
Abstract:Humans have a remarkable ability to disentangle complex sensory inputs (e.g., image, text) into simple factors of variation (e.g., shape, color) without much supervision. This ability has inspired many works that attempt to solve the following question: how do we invert the data generation process to extract those factors with minimal or no supervision? Several works in the literature on non-linear independent component analysis have established this negative result; without some knowledge of the data generation process or appropriate inductive biases, it is impossible to perform this inversion. In recent years, a lot of progress has been made on disentanglement under structural assumptions, e.g., when we have access to auxiliary information that makes the factors of variation conditionally independent. However, existing work requires a lot of auxiliary information, e.g., in supervised classification, it prescribes that the number of label classes should be at least equal to the total dimension of all factors of variation. In this work, we depart from these assumptions and ask: a) How can we get disentanglement when the auxiliary information does not provide conditional independence over the factors of variation? b) Can we reduce the amount of auxiliary information required for disentanglement? For a class of models where auxiliary information does not ensure conditional independence, we show theoretically and experimentally that disentanglement (to a large extent) is possible even when the auxiliary information dimension is much less than the dimension of the true latent representation.
Automatic Debiased Machine Learning for Dynamic Treatment Effects
Apr 09, 2022

Abstract:We extend the idea of automated debiased machine learning to the dynamic treatment regime. We show that the multiply robust formula for the dynamic treatment regime with discrete treatments can be re-stated in terms of a recursive Riesz representer characterization of nested mean regressions. We then apply a recursive Riesz representer estimation learning algorithm that estimates de-biasing corrections without the need to characterize how the correction terms look like, such as for instance, products of inverse probability weighting terms, as is done in prior work on doubly robust estimation in the dynamic regime. Our approach defines a sequence of loss minimization problems, whose minimizers are the mulitpliers of the de-biasing correction, hence circumventing the need for solving auxiliary propensity models and directly optimizing for the mean squared error of the target de-biasing correction.
Omitted Variable Bias in Machine Learned Causal Models
Dec 29, 2021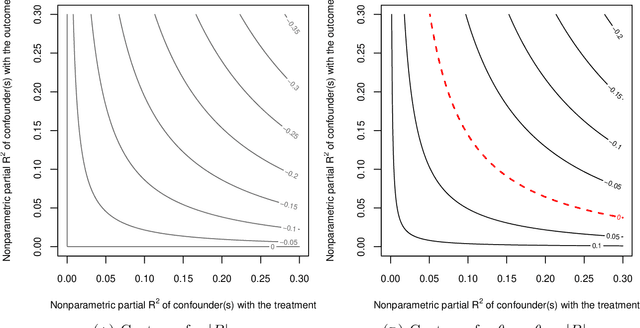
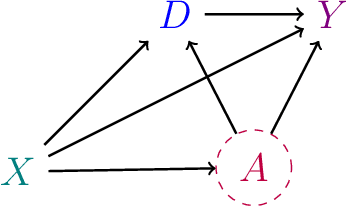
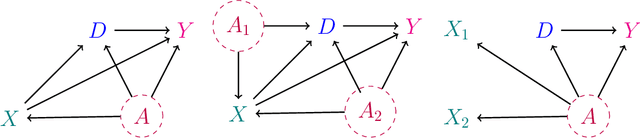
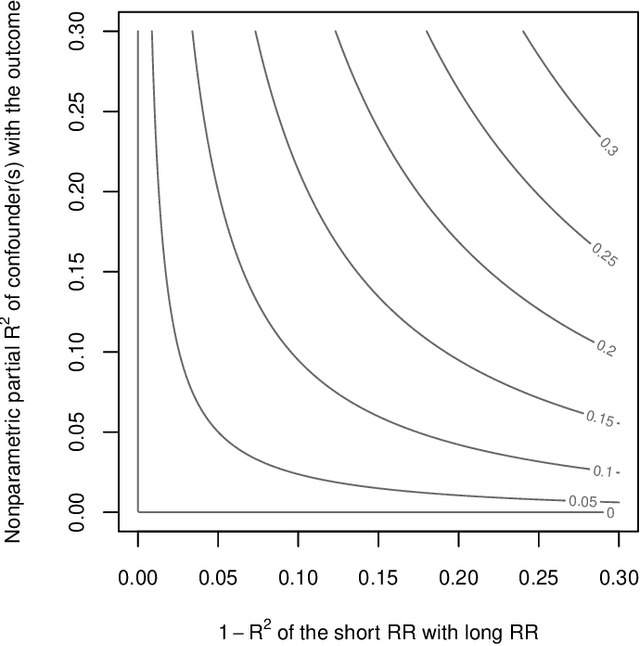
Abstract:We derive general, yet simple, sharp bounds on the size of the omitted variable bias for a broad class of causal parameters that can be identified as linear functionals of the conditional expectation function of the outcome. Such functionals encompass many of the traditional targets of investigation in causal inference studies, such as, for example, (weighted) average of potential outcomes, average treatment effects (including subgroup effects, such as the effect on the treated), (weighted) average derivatives, and policy effects from shifts in covariate distribution -- all for general, nonparametric causal models. Our construction relies on the Riesz-Frechet representation of the target functional. Specifically, we show how the bound on the bias depends only on the additional variation that the latent variables create both in the outcome and in the Riesz representer for the parameter of interest. Moreover, in many important cases (e.g, average treatment effects in partially linear models, or in nonseparable models with a binary treatment) the bound is shown to depend on two easily interpretable quantities: the nonparametric partial $R^2$ (Pearson's "correlation ratio") of the unobserved variables with the treatment and with the outcome. Therefore, simple plausibility judgments on the maximum explanatory power of omitted variables (in explaining treatment and outcome variation) are sufficient to place overall bounds on the size of the bias. Finally, leveraging debiased machine learning, we provide flexible and efficient statistical inference methods to estimate the components of the bounds that are identifiable from the observed distribution.
Robust Generalized Method of Moments: A Finite Sample Viewpoint
Oct 13, 2021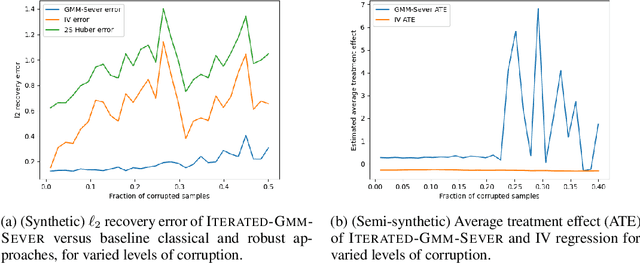
Abstract:For many inference problems in statistics and econometrics, the unknown parameter is identified by a set of moment conditions. A generic method of solving moment conditions is the Generalized Method of Moments (GMM). However, classical GMM estimation is potentially very sensitive to outliers. Robustified GMM estimators have been developed in the past, but suffer from several drawbacks: computational intractability, poor dimension-dependence, and no quantitative recovery guarantees in the presence of a constant fraction of outliers. In this work, we develop the first computationally efficient GMM estimator (under intuitive assumptions) that can tolerate a constant $\epsilon$ fraction of adversarially corrupted samples, and that has an $\ell_2$ recovery guarantee of $O(\sqrt{\epsilon})$. To achieve this, we draw upon and extend a recent line of work on algorithmic robust statistics for related but simpler problems such as mean estimation, linear regression and stochastic optimization. As two examples of the generality of our algorithm, we show how our estimation algorithm and assumptions apply to instrumental variables linear and logistic regression. Moreover, we experimentally validate that our estimator outperforms classical IV regression and two-stage Huber regression on synthetic and semi-synthetic datasets with corruption.
RieszNet and ForestRiesz: Automatic Debiased Machine Learning with Neural Nets and Random Forests
Oct 12, 2021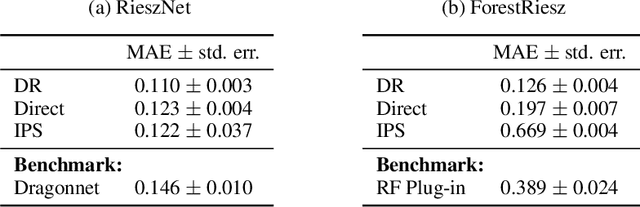
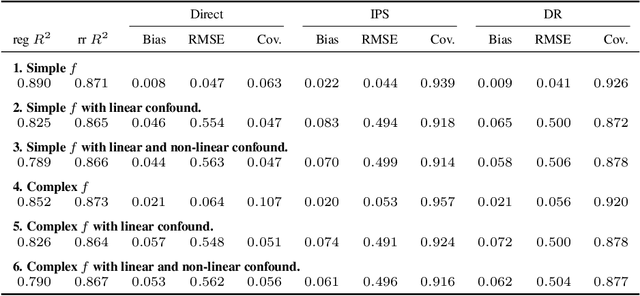
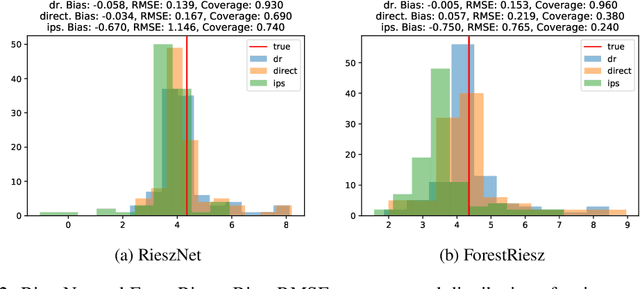
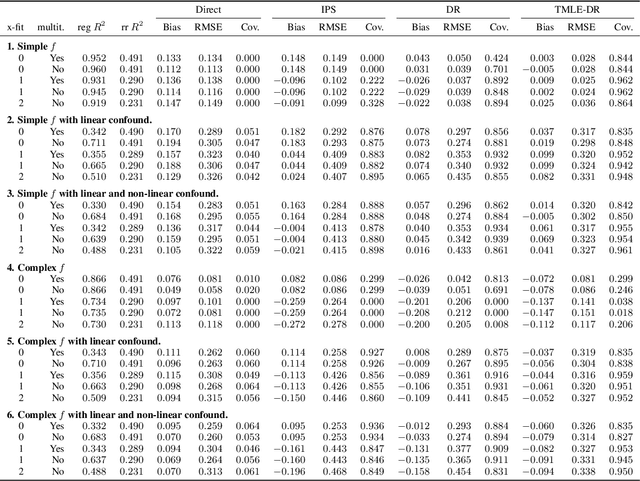
Abstract:Many causal and policy effects of interest are defined by linear functionals of high-dimensional or non-parametric regression functions. $\sqrt{n}$-consistent and asymptotically normal estimation of the object of interest requires debiasing to reduce the effects of regularization and/or model selection on the object of interest. Debiasing is typically achieved by adding a correction term to the plug-in estimator of the functional, that is derived based on a functional-specific theoretical derivation of what is known as the influence function and which leads to properties such as double robustness and Neyman orthogonality. We instead implement an automatic debiasing procedure based on automatically learning the Riesz representation of the linear functional using Neural Nets and Random Forests. Our method solely requires value query oracle access to the linear functional. We propose a multi-tasking Neural Net debiasing method with stochastic gradient descent minimization of a combined Riesz representer and regression loss, while sharing representation layers for the two functions. We also propose a Random Forest method which learns a locally linear representation of the Riesz function. Even though our methodology applies to arbitrary functionals, we experimentally find that it beats state of the art performance of the prior neural net based estimator of Shi et al. (2019) for the case of the average treatment effect functional. We also evaluate our method on the more challenging problem of estimating average marginal effects with continuous treatments, using semi-synthetic data of gasoline price changes on gasoline demand.
DoWhy: Addressing Challenges in Expressing and Validating Causal Assumptions
Aug 27, 2021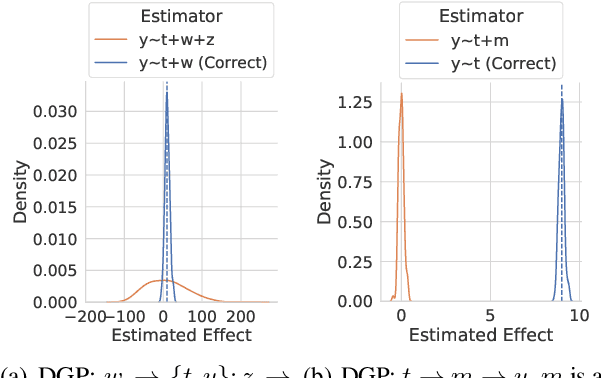
Abstract:Estimation of causal effects involves crucial assumptions about the data-generating process, such as directionality of effect, presence of instrumental variables or mediators, and whether all relevant confounders are observed. Violation of any of these assumptions leads to significant error in the effect estimate. However, unlike cross-validation for predictive models, there is no global validator method for a causal estimate. As a result, expressing different causal assumptions formally and validating them (to the extent possible) becomes critical for any analysis. We present DoWhy, a framework that allows explicit declaration of assumptions through a causal graph and provides multiple validation tests to check a subset of these assumptions. Our experience with DoWhy highlights a number of open questions for future research: developing new ways beyond causal graphs to express assumptions, the role of causal discovery in learning relevant parts of the graph, and developing validation tests that can better detect errors, both for average and conditional treatment effects. DoWhy is available at https://github.com/microsoft/dowhy.
Incentivizing Compliance with Algorithmic Instruments
Jul 28, 2021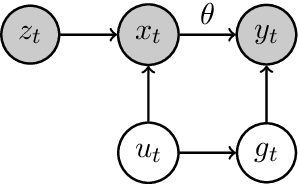
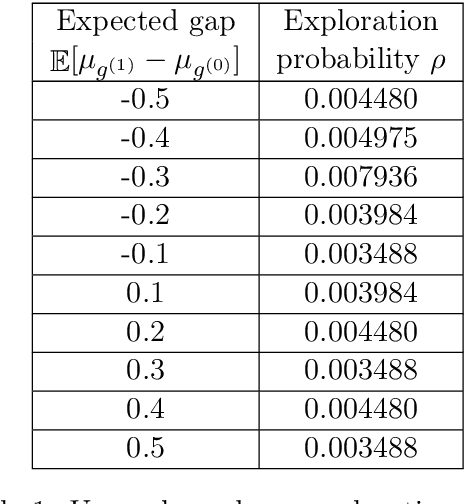
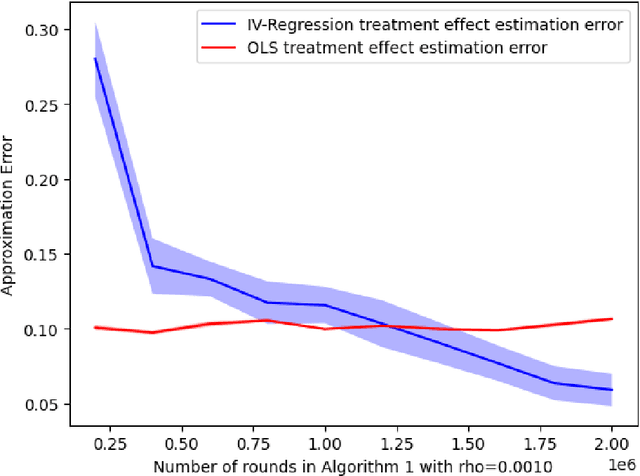
Abstract:Randomized experiments can be susceptible to selection bias due to potential non-compliance by the participants. While much of the existing work has studied compliance as a static behavior, we propose a game-theoretic model to study compliance as dynamic behavior that may change over time. In rounds, a social planner interacts with a sequence of heterogeneous agents who arrive with their unobserved private type that determines both their prior preferences across the actions (e.g., control and treatment) and their baseline rewards without taking any treatment. The planner provides each agent with a randomized recommendation that may alter their beliefs and their action selection. We develop a novel recommendation mechanism that views the planner's recommendation as a form of instrumental variable (IV) that only affects an agents' action selection, but not the observed rewards. We construct such IVs by carefully mapping the history -- the interactions between the planner and the previous agents -- to a random recommendation. Even though the initial agents may be completely non-compliant, our mechanism can incentivize compliance over time, thereby enabling the estimation of the treatment effect of each treatment, and minimizing the cumulative regret of the planner whose goal is to identify the optimal treatment.
Knowledge Distillation as Semiparametric Inference
Apr 20, 2021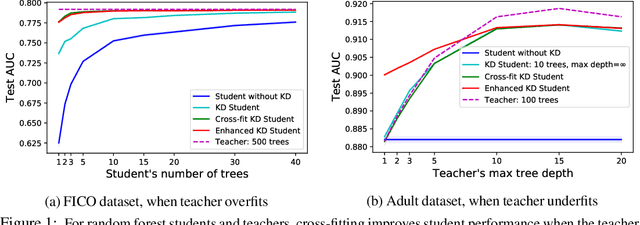

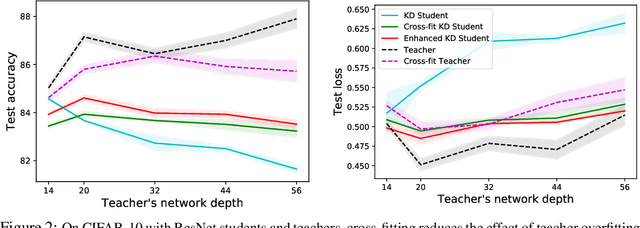
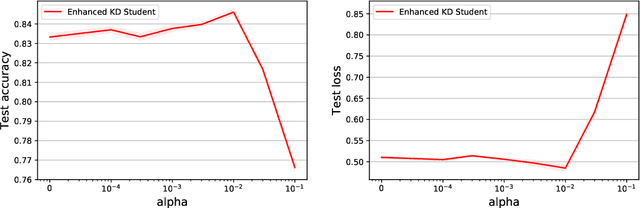
Abstract:A popular approach to model compression is to train an inexpensive student model to mimic the class probabilities of a highly accurate but cumbersome teacher model. Surprisingly, this two-step knowledge distillation process often leads to higher accuracy than training the student directly on labeled data. To explain and enhance this phenomenon, we cast knowledge distillation as a semiparametric inference problem with the optimal student model as the target, the unknown Bayes class probabilities as nuisance, and the teacher probabilities as a plug-in nuisance estimate. By adapting modern semiparametric tools, we derive new guarantees for the prediction error of standard distillation and develop two enhancements -- cross-fitting and loss correction -- to mitigate the impact of teacher overfitting and underfitting on student performance. We validate our findings empirically on both tabular and image data and observe consistent improvements from our knowledge distillation enhancements.
Estimating the Long-Term Effects of Novel Treatments
Mar 15, 2021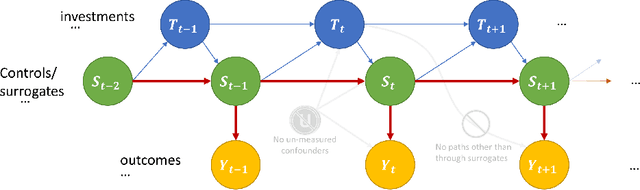
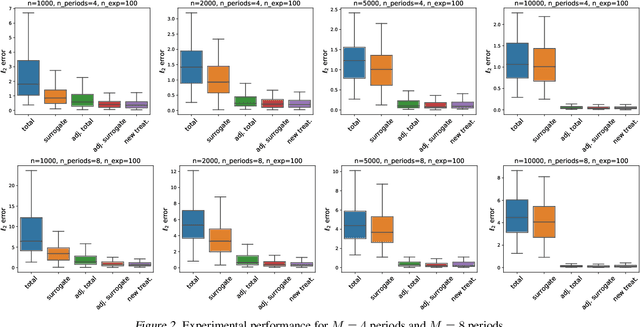


Abstract:Policy makers typically face the problem of wanting to estimate the long-term effects of novel treatments, while only having historical data of older treatment options. We assume access to a long-term dataset where only past treatments were administered and a short-term dataset where novel treatments have been administered. We propose a surrogate based approach where we assume that the long-term effect is channeled through a multitude of available short-term proxies. Our work combines three major recent techniques in the causal machine learning literature: surrogate indices, dynamic treatment effect estimation and double machine learning, in a unified pipeline. We show that our method is consistent and provides root-n asymptotically normal estimates under a Markovian assumption on the data and the observational policy. We use a data-set from a major corporation that includes customer investments over a three year period to create a semi-synthetic data distribution where the major qualitative properties of the real dataset are preserved. We evaluate the performance of our method and discuss practical challenges of deploying our formal methodology and how to address them.
Evidence-Based Policy Learning
Mar 12, 2021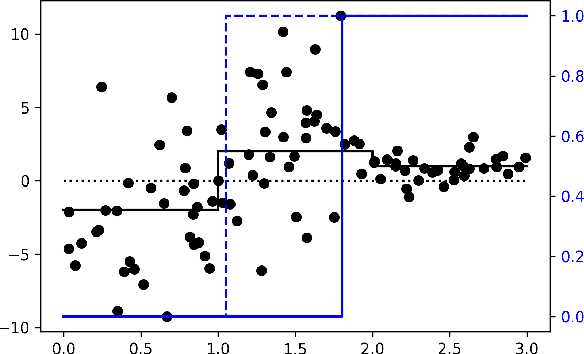
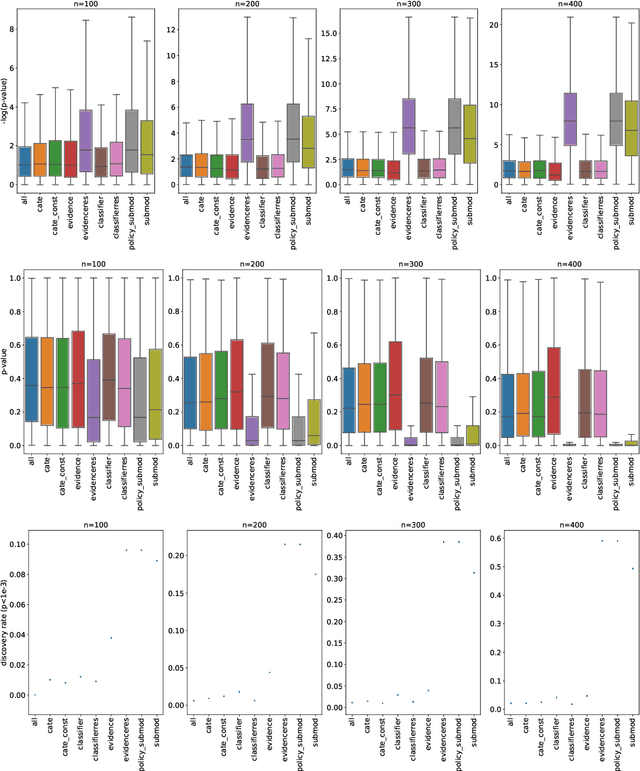
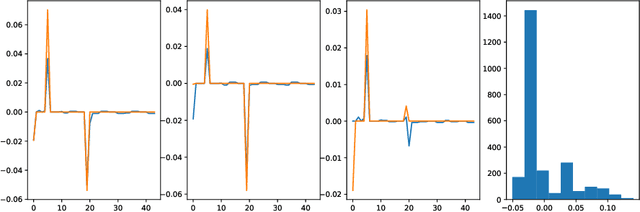
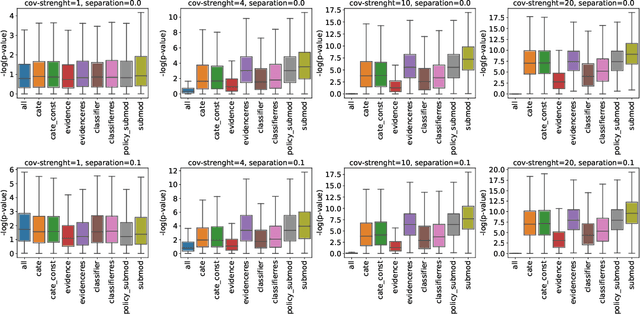
Abstract:The past years have seen seen the development and deployment of machine-learning algorithms to estimate personalized treatment-assignment policies from randomized controlled trials. Yet such algorithms for the assignment of treatment typically optimize expected outcomes without taking into account that treatment assignments are frequently subject to hypothesis testing. In this article, we explicitly take significance testing of the effect of treatment-assignment policies into account, and consider assignments that optimize the probability of finding a subset of individuals with a statistically significant positive treatment effect. We provide an efficient implementation using decision trees, and demonstrate its gain over selecting subsets based on positive (estimated) treatment effects. Compared to standard tree-based regression and classification tools, this approach tends to yield substantially higher power in detecting subgroups with positive treatment effects.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge