LMAct: A Benchmark for In-Context Imitation Learning with Long Multimodal Demonstrations

Today's largest foundation models have increasingly general capabilities, yet when used as agents, they often struggle with simple reasoning and decision-making tasks, even though they possess good factual knowledge of the task and how to solve it. In this paper, we present a benchmark to pressure-test these models' multimodal decision-making capabilities in the very long-context regime (up to one million tokens) and investigate whether they can learn from a large number of expert demonstrations in their context. We evaluate a wide range of state-of-the-art frontier models as policies across a battery of simple interactive decision-making tasks: playing tic-tac-toe, chess, and Atari, navigating grid worlds, solving crosswords, and controlling a simulated cheetah. We measure the performance of Claude 3.5 Sonnet, Gemini 1.5 Flash, Gemini 1.5 Pro, GPT-4o, o1-mini, and o1-preview under increasing amounts of expert demonstrations in the context $\unicode{x2013}$ from no demonstrations up to 512 full episodes, pushing these models' multimodal long-context reasoning capabilities to their limits. Across our tasks, today's frontier models rarely manage to fully reach expert performance, showcasing the difficulty of our benchmark. Presenting more demonstrations often has little effect, but some models steadily improve with more demonstrations on a few tasks. We investigate the effect of encoding observations as text or images and the impact of chain-of-thought prompting. Overall, our results suggest that even today's most capable models often struggle to imitate desired behavior by generalizing purely from in-context demonstrations. To help quantify the impact of other approaches and future innovations aiming to tackle this problem, we open source our benchmark that covers the zero-, few-, and many-shot regimes in a unified evaluation.

Compression via Pre-trained Transformers: A Study on Byte-Level Multimodal Data

Foundation models have recently been shown to be strong data compressors. However, when accounting for their excessive parameter count, their compression ratios are actually inferior to standard compression algorithms. Moreover, naively reducing the number of parameters may not necessarily help as it leads to worse predictions and thus weaker compression. In this paper, we conduct a large-scale empirical study to investigate whether there is a sweet spot where competitive compression ratios with pre-trained vanilla transformers are possible. To this end, we train families of models on 165GB of raw byte sequences of either text, image, or audio data (and all possible combinations of the three) and then compress 1GB of out-of-distribution (OOD) data from each modality. We find that relatively small models (i.e., millions of parameters) can outperform standard general-purpose compression algorithms (gzip, LZMA2) and even domain-specific compressors (PNG, JPEG 2000, FLAC) - even when factoring in parameter count. We achieve, e.g., the lowest compression ratio of 0.49 on OOD audio data (vs. 0.54 for FLAC). To study the impact of model- and dataset scale, we conduct extensive ablations and hyperparameter sweeps, and we investigate the effect of unimodal versus multimodal training. We find that even small models can be trained to perform well on multiple modalities, but, in contrast to previously reported results with large-scale foundation models, transfer to unseen modalities is generally weak.

Grandmaster-Level Chess Without Search

The recent breakthrough successes in machine learning are mainly attributed to scale: namely large-scale attention-based architectures and datasets of unprecedented scale. This paper investigates the impact of training at scale for chess. Unlike traditional chess engines that rely on complex heuristics, explicit search, or a combination of both, we train a 270M parameter transformer model with supervised learning on a dataset of 10 million chess games. We annotate each board in the dataset with action-values provided by the powerful Stockfish 16 engine, leading to roughly 15 billion data points. Our largest model reaches a Lichess blitz Elo of 2895 against humans, and successfully solves a series of challenging chess puzzles, without any domain-specific tweaks or explicit search algorithms. We also show that our model outperforms AlphaZero's policy and value networks (without MCTS) and GPT-3.5-turbo-instruct. A systematic investigation of model and dataset size shows that strong chess performance only arises at sufficient scale. To validate our results, we perform an extensive series of ablations of design choices and hyperparameters.

Learning Universal Predictors

Meta-learning has emerged as a powerful approach to train neural networks to learn new tasks quickly from limited data. Broad exposure to different tasks leads to versatile representations enabling general problem solving. But, what are the limits of meta-learning? In this work, we explore the potential of amortizing the most powerful universal predictor, namely Solomonoff Induction (SI), into neural networks via leveraging meta-learning to its limits. We use Universal Turing Machines (UTMs) to generate training data used to expose networks to a broad range of patterns. We provide theoretical analysis of the UTM data generation processes and meta-training protocols. We conduct comprehensive experiments with neural architectures (e.g. LSTMs, Transformers) and algorithmic data generators of varying complexity and universality. Our results suggest that UTM data is a valuable resource for meta-learning, and that it can be used to train neural networks capable of learning universal prediction strategies.

Language Modeling Is Compression

It has long been established that predictive models can be transformed into lossless compressors and vice versa. Incidentally, in recent years, the machine learning community has focused on training increasingly large and powerful self-supervised (language) models. Since these large language models exhibit impressive predictive capabilities, they are well-positioned to be strong compressors. In this work, we advocate for viewing the prediction problem through the lens of compression and evaluate the compression capabilities of large (foundation) models. We show that large language models are powerful general-purpose predictors and that the compression viewpoint provides novel insights into scaling laws, tokenization, and in-context learning. For example, Chinchilla 70B, while trained primarily on text, compresses ImageNet patches to 43.4% and LibriSpeech samples to 16.4% of their raw size, beating domain-specific compressors like PNG (58.5%) or FLAC (30.3%), respectively. Finally, we show that the prediction-compression equivalence allows us to use any compressor (like gzip) to build a conditional generative model.

Randomized Positional Encodings Boost Length Generalization of Transformers

Transformers have impressive generalization capabilities on tasks with a fixed context length. However, they fail to generalize to sequences of arbitrary length, even for seemingly simple tasks such as duplicating a string. Moreover, simply training on longer sequences is inefficient due to the quadratic computation complexity of the global attention mechanism. In this work, we demonstrate that this failure mode is linked to positional encodings being out-of-distribution for longer sequences (even for relative encodings) and introduce a novel family of positional encodings that can overcome this problem. Concretely, our randomized positional encoding scheme simulates the positions of longer sequences and randomly selects an ordered subset to fit the sequence's length. Our large-scale empirical evaluation of 6000 models across 15 algorithmic reasoning tasks shows that our method allows Transformers to generalize to sequences of unseen length (increasing test accuracy by 12.0% on average).

Memory-Based Meta-Learning on Non-Stationary Distributions

Memory-based meta-learning is a technique for approximating Bayes-optimal predictors. Under fairly general conditions, minimizing sequential prediction error, measured by the log loss, leads to implicit meta-learning. The goal of this work is to investigate how far this interpretation can be realized by current sequence prediction models and training regimes. The focus is on piecewise stationary sources with unobserved switching-points, which arguably capture an important characteristic of natural language and action-observation sequences in partially observable environments. We show that various types of memory-based neural models, including Transformers, LSTMs, and RNNs can learn to accurately approximate known Bayes-optimal algorithms and behave as if performing Bayesian inference over the latent switching-points and the latent parameters governing the data distribution within each segment.

Beyond Bayes-optimality: meta-learning what you know you don't know

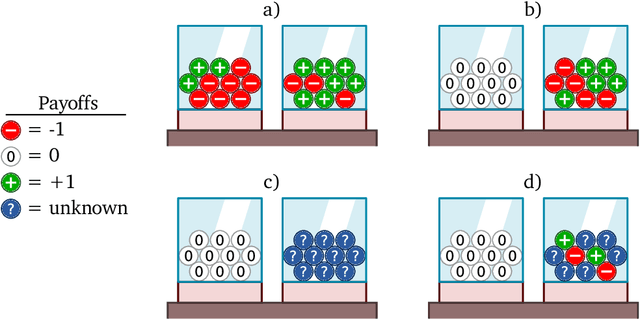
Meta-training agents with memory has been shown to culminate in Bayes-optimal agents, which casts Bayes-optimality as the implicit solution to a numerical optimization problem rather than an explicit modeling assumption. Bayes-optimal agents are risk-neutral, since they solely attune to the expected return, and ambiguity-neutral, since they act in new situations as if the uncertainty were known. This is in contrast to risk-sensitive agents, which additionally exploit the higher-order moments of the return, and ambiguity-sensitive agents, which act differently when recognizing situations in which they lack knowledge. Humans are also known to be averse to ambiguity and sensitive to risk in ways that aren't Bayes-optimal, indicating that such sensitivity can confer advantages, especially in safety-critical situations. How can we extend the meta-learning protocol to generate risk- and ambiguity-sensitive agents? The goal of this work is to fill this gap in the literature by showing that risk- and ambiguity-sensitivity also emerge as the result of an optimization problem using modified meta-training algorithms, which manipulate the experience-generation process of the learner. We empirically test our proposed meta-training algorithms on agents exposed to foundational classes of decision-making experiments and demonstrate that they become sensitive to risk and ambiguity.

Neural Networks and the Chomsky Hierarchy

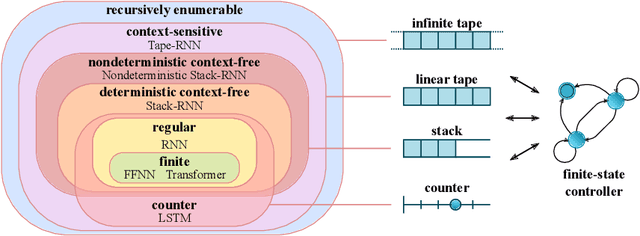
Reliable generalization lies at the heart of safe ML and AI. However, understanding when and how neural networks generalize remains one of the most important unsolved problems in the field. In this work, we conduct an extensive empirical study (2200 models, 16 tasks) to investigate whether insights from the theory of computation can predict the limits of neural network generalization in practice. We demonstrate that grouping tasks according to the Chomsky hierarchy allows us to forecast whether certain architectures will be able to generalize to out-of-distribution inputs. This includes negative results where even extensive amounts of data and training time never led to any non-trivial generalization, despite models having sufficient capacity to perfectly fit the training data. Our results show that, for our subset of tasks, RNNs and Transformers fail to generalize on non-regular tasks, LSTMs can solve regular and counter-language tasks, and only networks augmented with structured memory (such as a stack or memory tape) can successfully generalize on context-free and context-sensitive tasks.

Your Policy Regularizer is Secretly an Adversary

Policy regularization methods such as maximum entropy regularization are widely used in reinforcement learning to improve the robustness of a learned policy. In this paper, we show how this robustness arises from hedging against worst-case perturbations of the reward function, which are chosen from a limited set by an imagined adversary. Using convex duality, we characterize this robust set of adversarial reward perturbations under KL and alpha-divergence regularization, which includes Shannon and Tsallis entropy regularization as special cases. Importantly, generalization guarantees can be given within this robust set. We provide detailed discussion of the worst-case reward perturbations, and present intuitive empirical examples to illustrate this robustness and its relationship with generalization. Finally, we discuss how our analysis complements and extends previous results on adversarial reward robustness and path consistency optimality conditions.