Variational Regularized Unbalanced Optimal Transport: Single Network, Least Action

Recovering the dynamics from a few snapshots of a high-dimensional system is a challenging task in statistical physics and machine learning, with important applications in computational biology. Many algorithms have been developed to tackle this problem, based on frameworks such as optimal transport and the Schr\"odinger bridge. A notable recent framework is Regularized Unbalanced Optimal Transport (RUOT), which integrates both stochastic dynamics and unnormalized distributions. However, since many existing methods do not explicitly enforce optimality conditions, their solutions often struggle to satisfy the principle of least action and meet challenges to converge in a stable and reliable way. To address these issues, we propose Variational RUOT (Var-RUOT), a new framework to solve the RUOT problem. By incorporating the optimal necessary conditions for the RUOT problem into both the parameterization of the search space and the loss function design, Var-RUOT only needs to learn a scalar field to solve the RUOT problem and can search for solutions with lower action. We also examined the challenge of selecting a growth penalty function in the widely used Wasserstein-Fisher-Rao metric and proposed a solution that better aligns with biological priors in Var-RUOT. We validated the effectiveness of Var-RUOT on both simulated data and real single-cell datasets. Compared with existing algorithms, Var-RUOT can find solutions with lower action while exhibiting faster convergence and improved training stability.

Modeling Cell Dynamics and Interactions with Unbalanced Mean Field Schrödinger Bridge

Modeling the dynamics from sparsely time-resolved snapshot data is crucial for understanding complex cellular processes and behavior. Existing methods leverage optimal transport, Schr\"odinger bridge theory, or their variants to simultaneously infer stochastic, unbalanced dynamics from snapshot data. However, these approaches remain limited in their ability to account for cell-cell interactions. This integration is essential in real-world scenarios since intercellular communications are fundamental life processes and can influence cell state-transition dynamics. To address this challenge, we formulate the Unbalanced Mean-Field Schr\"odinger Bridge (UMFSB) framework to model unbalanced stochastic interaction dynamics from snapshot data. Inspired by this framework, we further propose CytoBridge, a deep learning algorithm designed to approximate the UMFSB problem. By explicitly modeling cellular transitions, proliferation, and interactions through neural networks, CytoBridge offers the flexibility to learn these processes directly from data. The effectiveness of our method has been extensively validated using both synthetic gene regulatory data and real scRNA-seq datasets. Compared to existing methods, CytoBridge identifies growth, transition, and interaction patterns, eliminates false transitions, and reconstructs the developmental landscape with greater accuracy.

Improving the Euclidean Diffusion Generation of Manifold Data by Mitigating Score Function Singularity

Euclidean diffusion models have achieved remarkable success in generative modeling across diverse domains, and they have been extended to manifold case in recent advances. Instead of explicitly utilizing the structure of special manifolds as studied in previous works, we investigate direct sampling of the Euclidean diffusion models for general manifold-constrained data in this paper. We reveal the multiscale singularity of the score function in the embedded space of manifold, which hinders the accuracy of diffusion-generated samples. We then present an elaborate theoretical analysis of the singularity structure of the score function by separating it along the tangential and normal directions of the manifold. To mitigate the singularity and improve the sampling accuracy, we propose two novel methods: (1) Niso-DM, which introduces non-isotropic noise along the normal direction to reduce scale discrepancies, and (2) Tango-DM, which trains only the tangential component of the score function using a tangential-only loss function. Numerical experiments demonstrate that our methods achieve superior performance on distributions over various manifolds with complex geometries.

Riemannian Denoising Diffusion Probabilistic Models

We propose Riemannian Denoising Diffusion Probabilistic Models (RDDPMs) for learning distributions on submanifolds of Euclidean space that are level sets of functions, including most of the manifolds relevant to applications. Existing methods for generative modeling on manifolds rely on substantial geometric information such as geodesic curves or eigenfunctions of the Laplace-Beltrami operator and, as a result, they are limited to manifolds where such information is available. In contrast, our method, built on a projection scheme, can be applied to more general manifolds, as it only requires being able to evaluate the value and the first order derivatives of the function that defines the submanifold. We provide a theoretical analysis of our method in the continuous-time limit, which elucidates the connection between our RDDPMs and score-based generative models on manifolds. The capability of our method is demonstrated on datasets from previous studies and on new datasets sampled from two high-dimensional manifolds, i.e. $\mathrm{SO}(10)$ and the configuration space of molecular system alanine dipeptide with fixed dihedral angle.

Integrating Dynamical Systems Modeling with Spatiotemporal scRNA-seq Data Analysis

Understanding the dynamic nature of biological systems is fundamental to deciphering cellular behavior, developmental processes, and disease progression. Single-cell RNA sequencing (scRNA-seq) has provided static snapshots of gene expression, offering valuable insights into cellular states at a single time point. Recent advancements in temporally resolved scRNA-seq, spatial transcriptomics (ST), and time-series spatial transcriptomics (temporal-ST) have further revolutionized our ability to study the spatiotemporal dynamics of individual cells. These technologies, when combined with computational frameworks such as Markov chains, stochastic differential equations (SDEs), and generative models like optimal transport and Schr\"odinger bridges, enable the reconstruction of dynamic cellular trajectories and cell fate decisions. This review discusses how these dynamical system approaches offer new opportunities to model and infer cellular dynamics from a systematic perspective.

Quasi-Newton OMP Approach for Super-Resolution Channel Estimation and Extrapolation

Channel estimation and extrapolation are fundamental issues in MIMO communication systems. In this paper, we proposed the quasi-Newton orthogonal matching pursuit (QNOMP) approach to overcome these issues with high efficiency while maintaining accuracy. The algorithm consists of two stages on the super-resolution recovery: we first performed a cheap on-grid OMP estimation of channel parameters in the sparsity domain (e.g., delay or angle), then an off-grid optimization to achieve the super-resolution. In the off-grid stage, we employed the BFGS quasi-Newton method to jointly estimate the parameters through a multipath model, which improved the speed and accuracy significantly. Furthermore, we derived the optimal extrapolated solution in the linear minimum mean squared estimator criterion, revealed its connection with Slepian basis, and presented a practical algorithm to realize the extrapolation based on the QNOMP results. Special treatment utilizing the block sparsity nature of the considered channels was also proposed. Numerical experiments on the simulated models and CDL-C channels demonstrated the high performance and low computational complexity of QNOMP.

Learning Stochastic Dynamics from Snapshots through Regularized Unbalanced Optimal Transport

Reconstructing dynamics using samples from sparsely time-resolved snapshots is an important problem in both natural sciences and machine learning. Here, we introduce a new deep learning approach for solving regularized unbalanced optimal transport (RUOT) and inferring continuous unbalanced stochastic dynamics from observed snapshots. Based on the RUOT form, our method models these dynamics without requiring prior knowledge of growth and death processes or additional information, allowing them to be learnt directly from data. Theoretically, we explore the connections between the RUOT and Schr\"odinger bridge problem and discuss the key challenges and potential solutions. The effectiveness of our method is demonstrated with a synthetic gene regulatory network. Compared with other methods, our approach accurately identifies growth and transition patterns, eliminates false transitions, and constructs the Waddington developmental landscape.

DMRA: An Adaptive Line Spectrum Estimation Method through Dynamical Multi-Resolution of Atoms

We proposed a novel dense line spectrum super-resolution algorithm, the DMRA, that leverages dynamical multi-resolution of atoms technique to address the limitation of traditional compressed sensing methods when handling dense point-source signals. The algorithm utilizes a smooth $\tanh$ relaxation function to replace the $\ell_0$ norm, promoting sparsity and jointly estimating the frequency atoms and complex gains. To reduce computational complexity and improve frequency estimation accuracy, a two-stage strategy was further introduced to dynamically adjust the number of the optimized degrees of freedom. The strategy first increases candidate frequencies through local refinement, then applies a sparse selector to eliminate insignificant frequencies, thereby adaptively adjusting the degrees of freedom to improve estimation accuracy. Theoretical analysis were provided to validate the proposed method for multi-parameter estimations. Computational results demonstrated that this algorithm achieves good super-resolution performance in various practical scenarios and outperforms the state-of-the-art methods in terms of frequency estimation accuracy and computational efficiency.

EPR-Net: Constructing non-equilibrium potential landscape via a variational force projection formulation

We present a novel yet simple deep learning approach, dubbed EPR-Net, for constructing the potential landscape of high-dimensional non-equilibrium steady state (NESS) systems. The key idea of our approach is to utilize the fact that the negative potential gradient is the orthogonal projection of the driving force in a weighted Hilbert space with respect to the steady-state distribution. The constructed loss function also coincides with the entropy production rate (EPR) formula in NESS theory. This approach can be extended to dealing with dimensionality reduction and state-dependent diffusion coefficients in a unified fashion. The robustness and effectiveness of the proposed approach are demonstrated by numerical studies of several high-dimensional biophysical models with multi-stability, limit cycle, or strange attractor with non-vanishing noise.

Intrinsically Motivated Self-supervised Learning in Reinforcement Learning

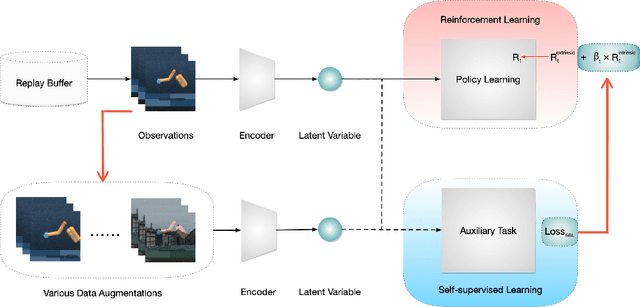
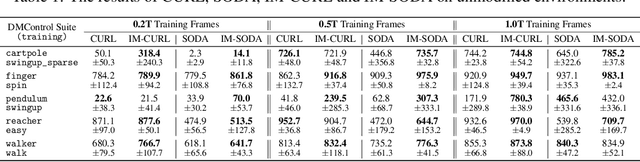
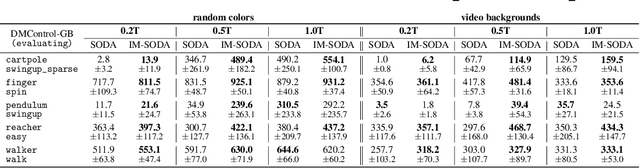
In vision-based reinforcement learning (RL) tasks, it is prevalent to assign the auxiliary task with a surrogate self-supervised loss so as to obtain more semantic representations and improve sample efficiency. However, abundant information in self-supervised auxiliary tasks has been disregarded, since the representation learning part and the decision-making part are separated. To sufficiently utilize information in the auxiliary task, we present a simple yet effective idea to employ self-supervised loss as an intrinsic reward, called Intrinsically Motivated Self-Supervised learning in Reinforcement learning (IM-SSR). We formally show that the self-supervised loss can be decomposed as exploration for novel states and robustness improvement from nuisance elimination. IM-SSR can be effortlessly plugged into any reinforcement learning with self-supervised auxiliary objectives with nearly no additional cost. Combined with IM-SSR, the previous underlying algorithms achieve salient improvements on both sample efficiency and generalization in various vision-based robotics tasks from the DeepMind Control Suite, especially when the reward signal is sparse.