Stephen Roberts
Semi-unsupervised Learning of Human Activity using Deep Generative Models
Oct 29, 2018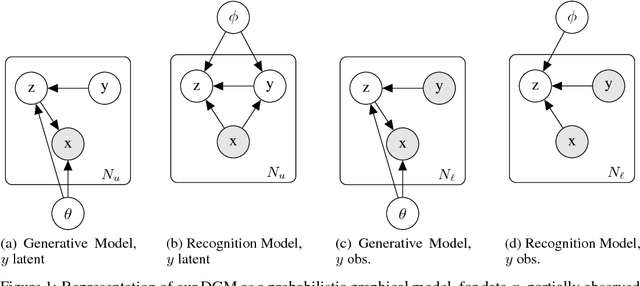
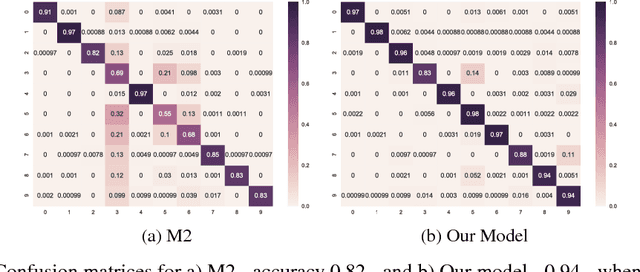
Abstract:Here we demonstrate a new deep generative model for classification. We introduce `semi-unsupervised learning', a problem regime related to transfer learning and zero/few shot learning where, in the training data, some classes are sparsely labelled and others entirely unlabelled. Models able to learn from training data of this type are potentially of great use, as many medical datasets are `semi-unsupervised'. Our model demonstrates superior semi-unsupervised classification performance on MNIST to model M2 from Kingma and Welling (2014). We apply the model to human accelerometer data, performing activity classification and structure discovery on windows of time series data.
MOrdReD: Memory-based Ordinal Regression Deep Neural Networks for Time Series Forecasting
Oct 24, 2018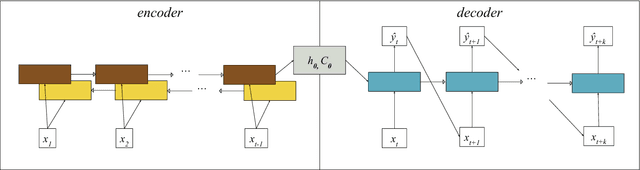


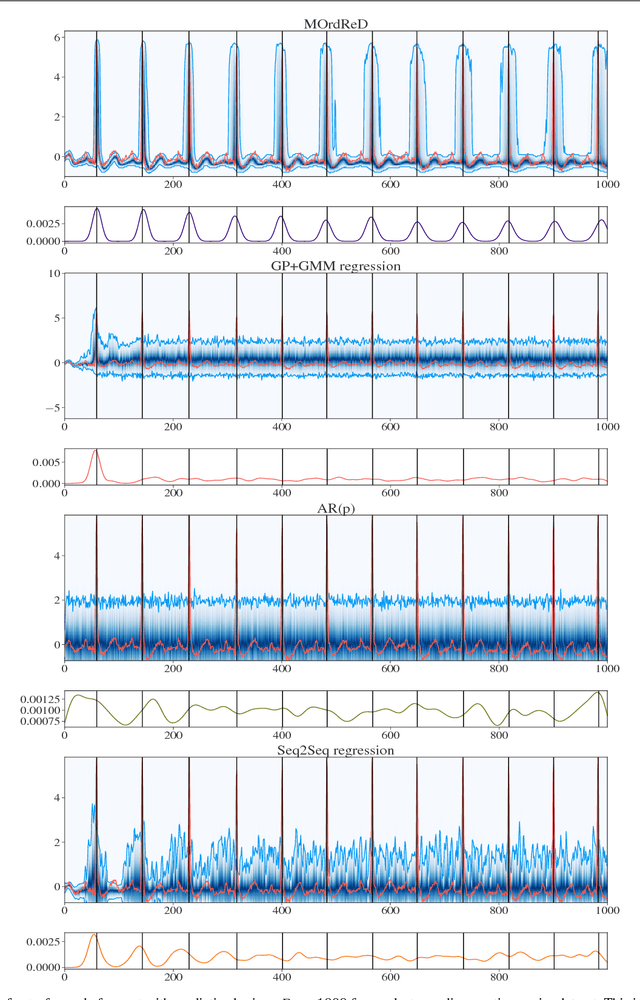
Abstract:Time series forecasting is ubiquitous in the modern world. Applications range from health care to astronomy, and include climate modelling, financial trading and monitoring of critical engineering equipment. To offer value over this range of activities, models must not only provide accurate forecasts, but also quantify and adjust their uncertainty over time. In this work, we directly tackle this task with a novel, fully end-to-end deep learning method for time series forecasting. By recasting time series forecasting as an ordinal regression task, we develop a principled methodology to assess long-term predictive uncertainty and describe rich multimodal, non-Gaussian behaviour, which arises regularly in applied settings. Notably, our framework is a wholly general-purpose approach that requires little to no user intervention to be used. We showcase this key feature in a large-scale benchmark test with 45 datasets drawn from both, a wide range of real-world application domains, as well as a comprehensive list of synthetic maps. This wide comparison encompasses state-of-the-art methods in both the Machine Learning and Statistics modelling literature, such as the Gaussian Process. We find that our approach does not only provide excellent predictive forecasts, shadowing true future values, but also allows us to infer valuable information, such as the predictive distribution of the occurrence of critical events of interest, accurately and reliably even over long time horizons.
Equality Constrained Decision Trees: For the Algorithmic Enforcement of Group Fairness
Oct 10, 2018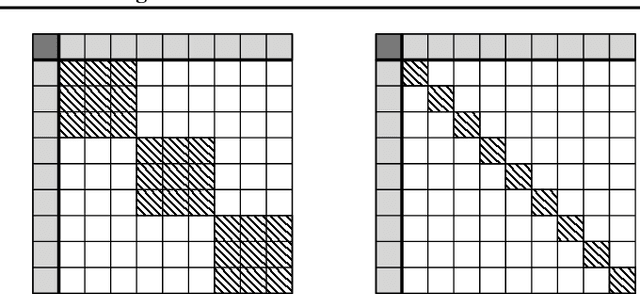
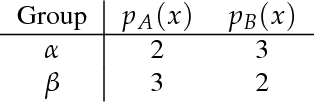
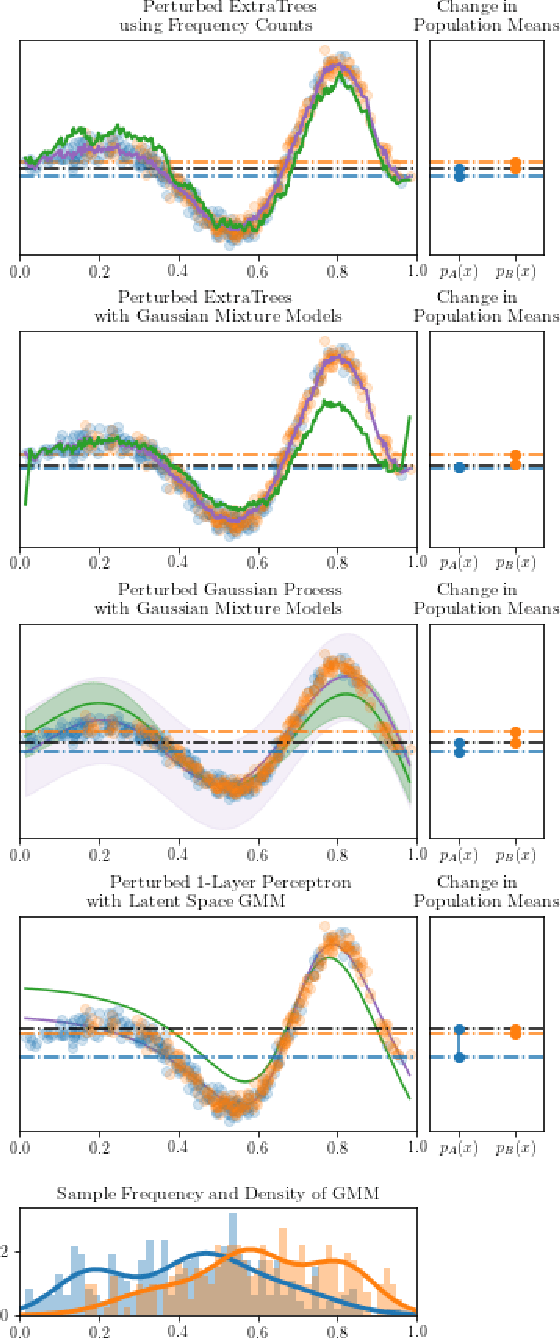

Abstract:Fairness, through its many forms and definitions, has become an important issue facing the machine learning community. In this work, we consider how to incorporate group fairness constraints in kernel regression methods. More specifically, we focus on examining the incorporation of these constraints in decision tree regression when cast as a form of kernel regression, with direct applications to random forests and boosted trees amongst other widespread popular inference techniques. We show that order of complexity of memory and computation is preserved for such models and bounds the expected perturbations to the model in terms of the number of leaves of the trees. Importantly, the approach works on trained models and hence can be easily applied to models in current use.
Sequential sampling of Gaussian process latent variable models
Jul 20, 2018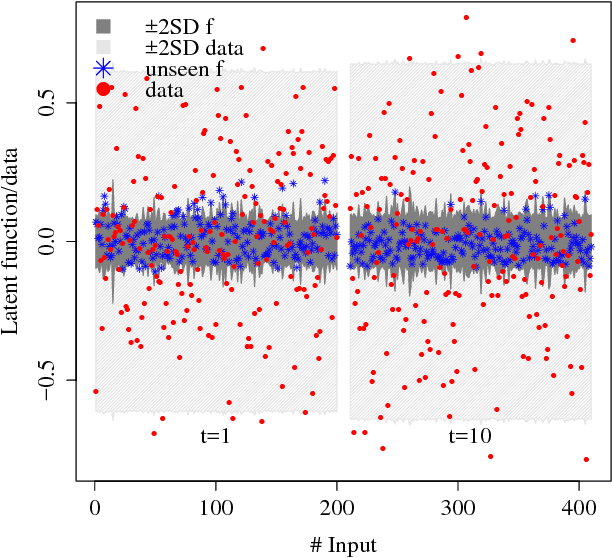
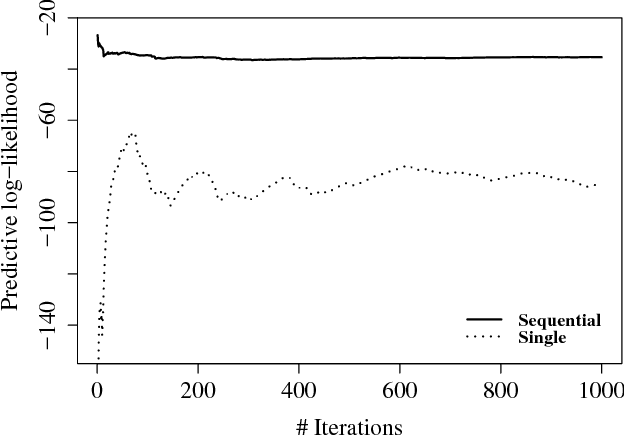
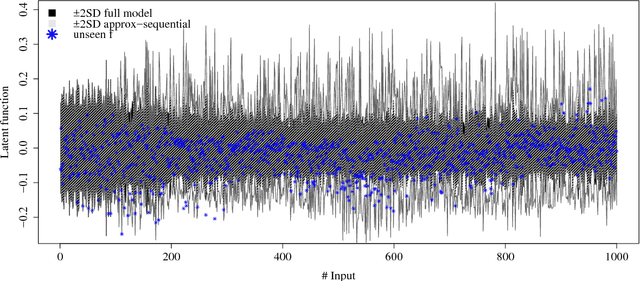
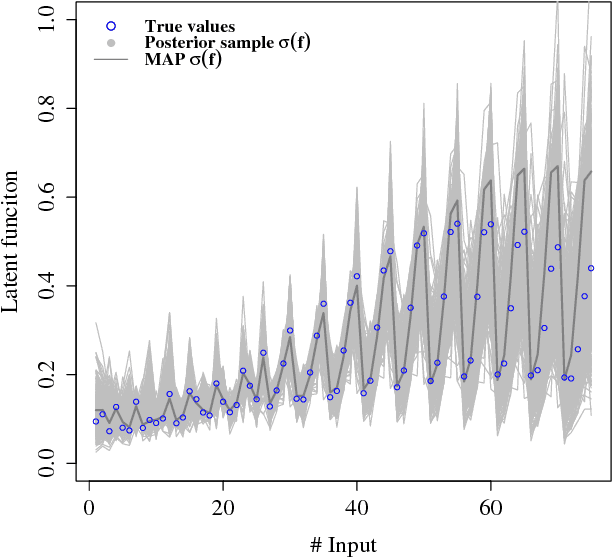
Abstract:We consider the problem of inferring a latent function in a probabilistic model of data. When dependencies of the latent function are specified by a Gaussian process and the data likelihood is complex, efficient computation often involve Markov chain Monte Carlo sampling with limited applicability to large data sets. We extend some of these techniques to scale efficiently when the problem exhibits a sequential structure. We propose an approximation that enables sequential sampling of both latent variables and associated parameters. We demonstrate strong performance in growing-data settings that would otherwise be unfeasible with naive, non-sequential sampling.
Extracting Predictive Information from Heterogeneous Data Streams using Gaussian Processes
Jul 11, 2018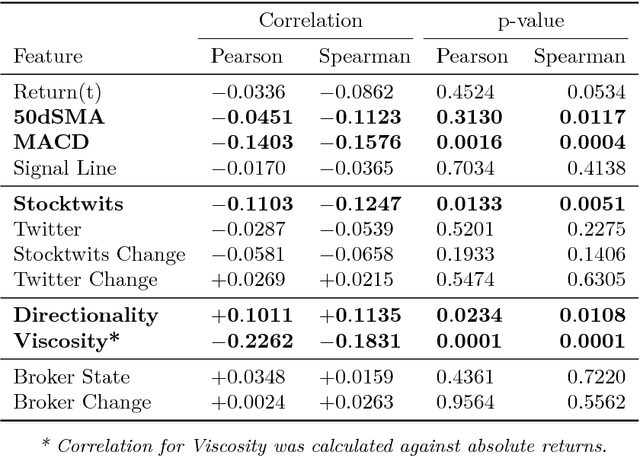
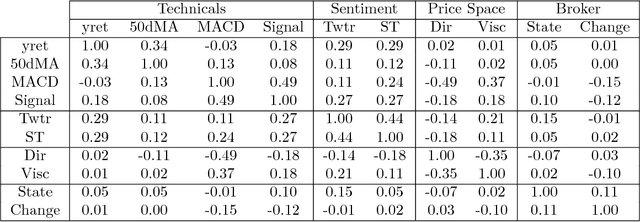
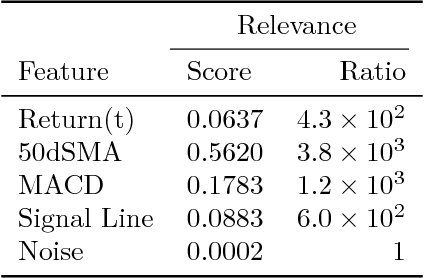
Abstract:Financial markets are notoriously complex environments, presenting vast amounts of noisy, yet potentially informative data. We consider the problem of forecasting financial time series from a wide range of information sources using online Gaussian Processes with Automatic Relevance Determination (ARD) kernels. We measure the performance gain, quantified in terms of Normalised Root Mean Square Error (NRMSE), Median Absolute Deviation (MAD) and Pearson correlation, from fusing each of four separate data domains: time series technicals, sentiment analysis, options market data and broker recommendations. We show evidence that ARD kernels produce meaningful feature rankings that help retain salient inputs and reduce input dimensionality, providing a framework for sifting through financial complexity. We measure the performance gain from fusing each domain's heterogeneous data streams into a single probabilistic model. In particular our findings highlight the critical value of options data in mapping out the curvature of price space and inspire an intuitive, novel direction for research in financial prediction.
Entropic Spectral Learning in Large Scale Networks
Apr 18, 2018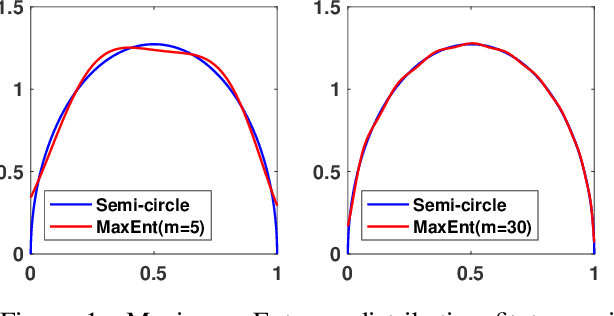

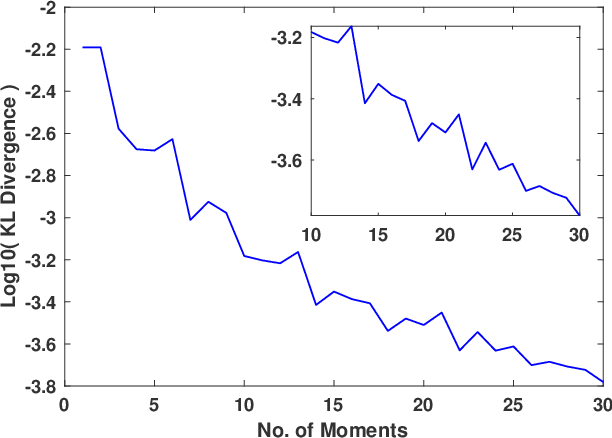
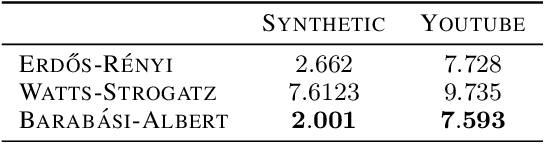
Abstract:We present a novel algorithm for learning the spectral density of large scale networks using stochastic trace estimation and the method of maximum entropy. The complexity of the algorithm is linear in the number of non-zero elements of the matrix, offering a computational advantage over other algorithms. We apply our algorithm to the problem of community detection in large networks. We show state-of-the-art performance on both synthetic and real datasets.
Gradient descent in Gaussian random fields as a toy model for high-dimensional optimisation in deep learning
Mar 24, 2018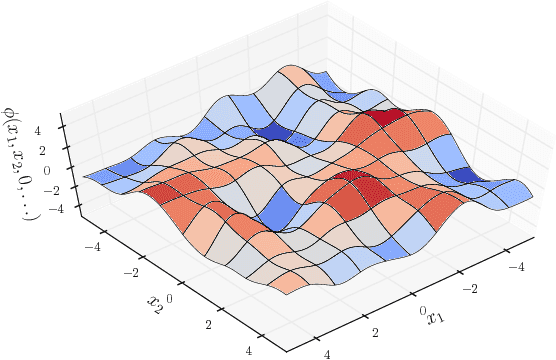
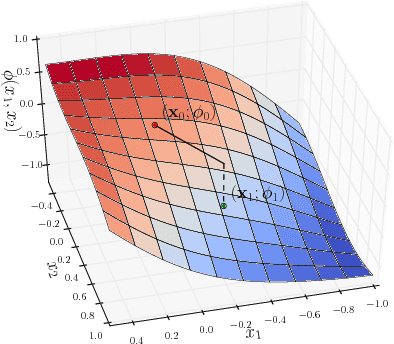
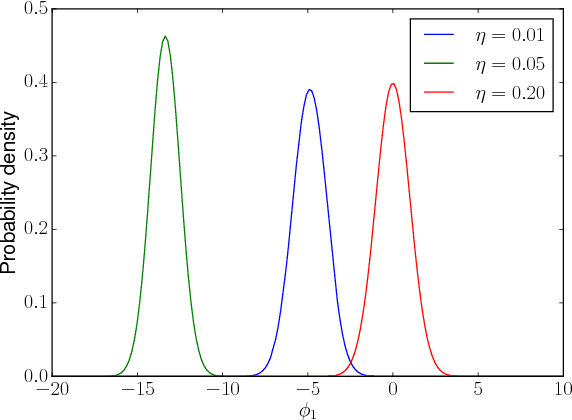
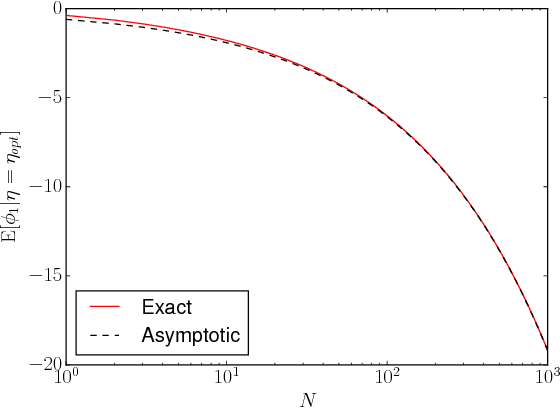
Abstract:In this paper we model the loss function of high-dimensional optimization problems by a Gaussian random field, or equivalently a Gaussian process. Our aim is to study gradient descent in such loss functions or energy landscapes and compare it to results obtained from real high-dimensional optimization problems such as encountered in deep learning. In particular, we analyze the distribution of the improved loss function after a step of gradient descent, provide analytic expressions for the moments as well as prove asymptotic normality as the dimension of the parameter space becomes large. Moreover, we compare this with the expectation of the global minimum of the landscape obtained by means of the Euler characteristic of excursion sets. Besides complementing our analytical findings with numerical results from simulated Gaussian random fields, we also compare it to loss functions obtained from optimisation problems on synthetic and real data sets by proposing a "black box" random field toy-model for a deep neural network loss function.
VBALD - Variational Bayesian Approximation of Log Determinants
Feb 21, 2018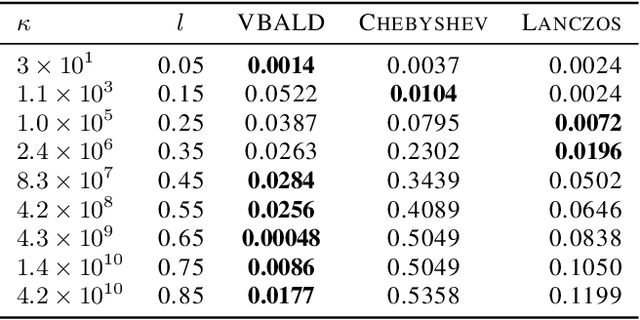
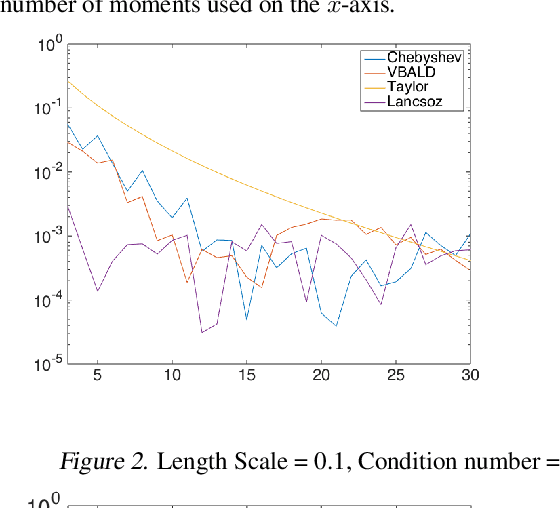
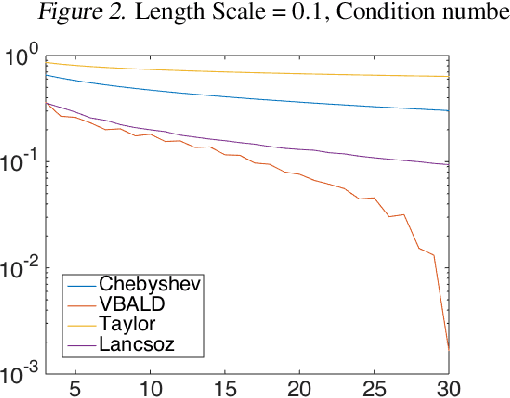

Abstract:Evaluating the log determinant of a positive definite matrix is ubiquitous in machine learning. Applications thereof range from Gaussian processes, minimum-volume ellipsoids, metric learning, kernel learning, Bayesian neural networks, Determinental Point Processes, Markov random fields to partition functions of discrete graphical models. In order to avoid the canonical, yet prohibitive, Cholesky $\mathcal{O}(n^{3})$ computational cost, we propose a novel approach, with complexity $\mathcal{O}(n^{2})$, based on a constrained variational Bayes algorithm. We compare our method to Taylor, Chebyshev and Lanczos approaches and show state of the art performance on both synthetic and real-world datasets.
Safe Policy Search with Gaussian Process Models
Dec 15, 2017
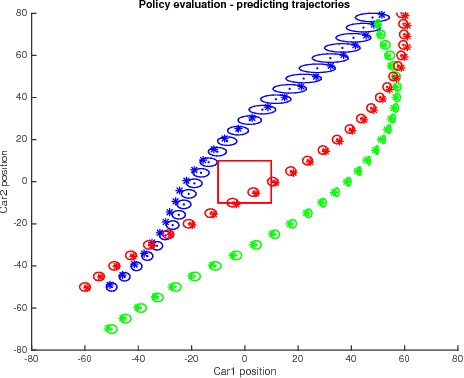
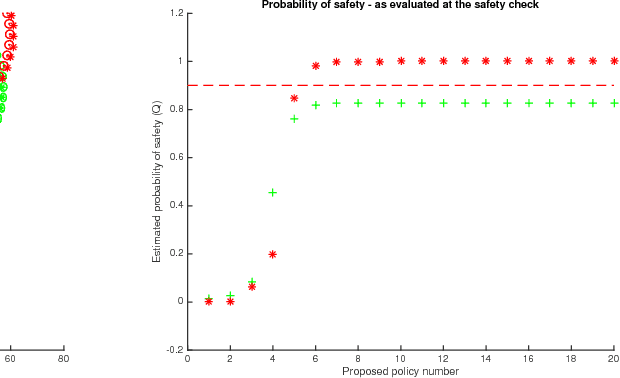
Abstract:We propose a method to optimise the parameters of a policy which will be used to safely perform a given task in a data-efficient manner. We train a Gaussian process model to capture the system dynamics, based on the PILCO framework. Our model has useful analytic properties, which allow closed form computation of error gradients and estimating the probability of violating given state space constraints. During training, as well as operation, only policies that are deemed safe are implemented on the real system, minimising the risk of failure.
Cost-sensitive detection with variational autoencoders for environmental acoustic sensing
Dec 07, 2017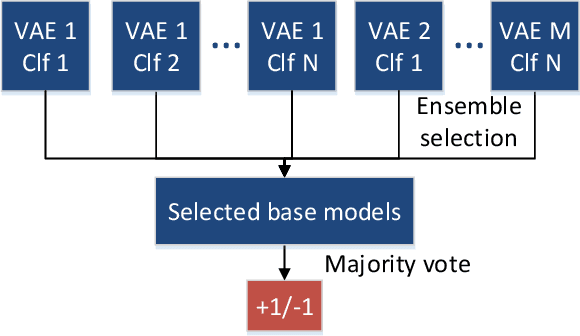

Abstract:Environmental acoustic sensing involves the retrieval and processing of audio signals to better understand our surroundings. While large-scale acoustic data make manual analysis infeasible, they provide a suitable playground for machine learning approaches. Most existing machine learning techniques developed for environmental acoustic sensing do not provide flexible control of the trade-off between the false positive rate and the false negative rate. This paper presents a cost-sensitive classification paradigm, in which the hyper-parameters of classifiers and the structure of variational autoencoders are selected in a principled Neyman-Pearson framework. We examine the performance of the proposed approach using a dataset from the HumBug project which aims to detect the presence of mosquitoes using sound collected by simple embedded devices.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge