Beyond Euclid: An Illustrated Guide to Modern Machine Learning with Geometric, Topological, and Algebraic Structures

The enduring legacy of Euclidean geometry underpins classical machine learning, which, for decades, has been primarily developed for data lying in Euclidean space. Yet, modern machine learning increasingly encounters richly structured data that is inherently nonEuclidean. This data can exhibit intricate geometric, topological and algebraic structure: from the geometry of the curvature of space-time, to topologically complex interactions between neurons in the brain, to the algebraic transformations describing symmetries of physical systems. Extracting knowledge from such non-Euclidean data necessitates a broader mathematical perspective. Echoing the 19th-century revolutions that gave rise to non-Euclidean geometry, an emerging line of research is redefining modern machine learning with non-Euclidean structures. Its goal: generalizing classical methods to unconventional data types with geometry, topology, and algebra. In this review, we provide an accessible gateway to this fast-growing field and propose a graphical taxonomy that integrates recent advances into an intuitive unified framework. We subsequently extract insights into current challenges and highlight exciting opportunities for future development in this field.

The Selective G-Bispectrum and its Inversion: Applications to G-Invariant Networks

An important problem in signal processing and deep learning is to achieve \textit{invariance} to nuisance factors not relevant for the task. Since many of these factors are describable as the action of a group $G$ (e.g. rotations, translations, scalings), we want methods to be $G$-invariant. The $G$-Bispectrum extracts every characteristic of a given signal up to group action: for example, the shape of an object in an image, but not its orientation. Consequently, the $G$-Bispectrum has been incorporated into deep neural network architectures as a computational primitive for $G$-invariance\textemdash akin to a pooling mechanism, but with greater selectivity and robustness. However, the computational cost of the $G$-Bispectrum ($\mathcal{O}(|G|^2)$, with $|G|$ the size of the group) has limited its widespread adoption. Here, we show that the $G$-Bispectrum computation contains redundancies that can be reduced into a \textit{selective $G$-Bispectrum} with $\mathcal{O}(|G|)$ complexity. We prove desirable mathematical properties of the selective $G$-Bispectrum and demonstrate how its integration in neural networks enhances accuracy and robustness compared to traditional approaches, while enjoying considerable speeds-up compared to the full $G$-Bispectrum.

Harmonics of Learning: Universal Fourier Features Emerge in Invariant Networks

In this work, we formally prove that, under certain conditions, if a neural network is invariant to a finite group then its weights recover the Fourier transform on that group. This provides a mathematical explanation for the emergence of Fourier features -- a ubiquitous phenomenon in both biological and artificial learning systems. The results hold even for non-commutative groups, in which case the Fourier transform encodes all the irreducible unitary group representations. Our findings have consequences for the problem of symmetry discovery. Specifically, we demonstrate that the algebraic structure of an unknown group can be recovered from the weights of a network that is at least approximately invariant within certain bounds. Overall, this work contributes to a foundation for an algebraic learning theory of invariant neural network representations.

Exploring the hierarchical structure of human plans via program generation

Human behavior is inherently hierarchical, resulting from the decomposition of a task into subtasks or an abstract action into concrete actions. However, behavior is typically measured as a sequence of actions, which makes it difficult to infer its hierarchical structure. In this paper, we explore how people form hierarchically-structured plans, using an experimental paradigm that makes hierarchical representations observable: participants create programs that produce sequences of actions in a language with explicit hierarchical structure. This task lets us test two well-established principles of human behavior: utility maximization (i.e. using fewer actions) and minimum description length (MDL; i.e. having a shorter program). We find that humans are sensitive to both metrics, but that both accounts fail to predict a qualitative feature of human-created programs, namely that people prefer programs with reuse over and above the predictions of MDL. We formalize this preference for reuse by extending the MDL account into a generative model over programs, modeling hierarchy choice as the induction of a grammar over actions. Our account can explain the preference for reuse and provides the best prediction of human behavior, going beyond simple accounts of compressibility to highlight a principle that guides hierarchical planning.

A General Framework for Robust G-Invariance in G-Equivariant Networks

We introduce a general method for achieving robust group-invariance in group-equivariant convolutional neural networks ($G$-CNNs), which we call the $G$-triple-correlation ($G$-TC) layer. The approach leverages the theory of the triple-correlation on groups, which is the unique, lowest-degree polynomial invariant map that is also complete. Many commonly used invariant maps - such as the max - are incomplete: they remove both group and signal structure. A complete invariant, by contrast, removes only the variation due to the actions of the group, while preserving all information about the structure of the signal. The completeness of the triple correlation endows the $G$-TC layer with strong robustness, which can be observed in its resistance to invariance-based adversarial attacks. In addition, we observe that it yields measurable improvements in classification accuracy over standard Max $G$-Pooling in $G$-CNN architectures. We provide a general and efficient implementation of the method for any discretized group, which requires only a table defining the group's product structure. We demonstrate the benefits of this method for $G$-CNNs defined on both commutative and non-commutative groups - $SO(2)$, $O(2)$, $SO(3)$, and $O(3)$ (discretized as the cyclic $C8$, dihedral $D16$, chiral octahedral $O$ and full octahedral $O_h$ groups) - acting on $\mathbb{R}^2$ and $\mathbb{R}^3$ on both $G$-MNIST and $G$-ModelNet10 datasets.

Identifying Interpretable Visual Features in Artificial and Biological Neural Systems

Single neurons in neural networks are often interpretable in that they represent individual, intuitively meaningful features. However, many neurons exhibit $\textit{mixed selectivity}$, i.e., they represent multiple unrelated features. A recent hypothesis proposes that features in deep networks may be represented in $\textit{superposition}$, i.e., on non-orthogonal axes by multiple neurons, since the number of possible interpretable features in natural data is generally larger than the number of neurons in a given network. Accordingly, we should be able to find meaningful directions in activation space that are not aligned with individual neurons. Here, we propose (1) an automated method for quantifying visual interpretability that is validated against a large database of human psychophysics judgments of neuron interpretability, and (2) an approach for finding meaningful directions in network activation space. We leverage these methods to discover directions in convolutional neural networks that are more intuitively meaningful than individual neurons, as we confirm and investigate in a series of analyses. Moreover, we apply the same method to three recent datasets of visual neural responses in the brain and find that our conclusions largely transfer to real neural data, suggesting that superposition might be deployed by the brain. This also provides a link with disentanglement and raises fundamental questions about robust, efficient and factorized representations in both artificial and biological neural systems.

ICML 2023 Topological Deep Learning Challenge : Design and Results

This paper presents the computational challenge on topological deep learning that was hosted within the ICML 2023 Workshop on Topology and Geometry in Machine Learning. The competition asked participants to provide open-source implementations of topological neural networks from the literature by contributing to the python packages TopoNetX (data processing) and TopoModelX (deep learning). The challenge attracted twenty-eight qualifying submissions in its two-month duration. This paper describes the design of the challenge and summarizes its main findings.

Architectures of Topological Deep Learning: A Survey on Topological Neural Networks

The natural world is full of complex systems characterized by intricate relations between their components: from social interactions between individuals in a social network to electrostatic interactions between atoms in a protein. Topological Deep Learning (TDL) provides a comprehensive framework to process and extract knowledge from data associated with these systems, such as predicting the social community to which an individual belongs or predicting whether a protein can be a reasonable target for drug development. TDL has demonstrated theoretical and practical advantages that hold the promise of breaking ground in the applied sciences and beyond. However, the rapid growth of the TDL literature has also led to a lack of unification in notation and language across Topological Neural Network (TNN) architectures. This presents a real obstacle for building upon existing works and for deploying TNNs to new real-world problems. To address this issue, we provide an accessible introduction to TDL, and compare the recently published TNNs using a unified mathematical and graphical notation. Through an intuitive and critical review of the emerging field of TDL, we extract valuable insights into current challenges and exciting opportunities for future development.

Bispectral Neural Networks

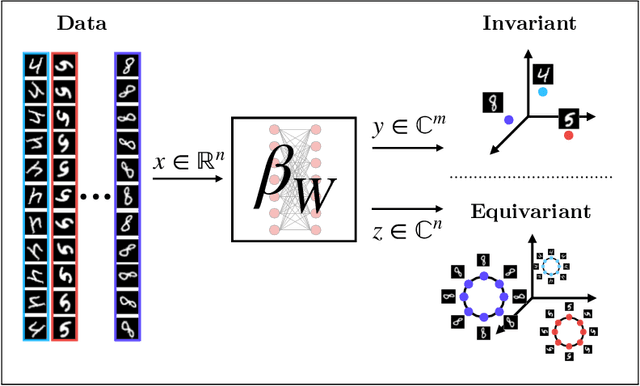
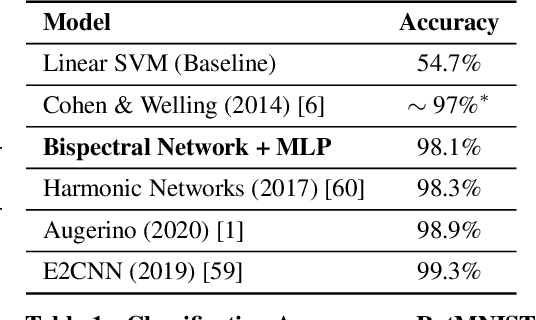
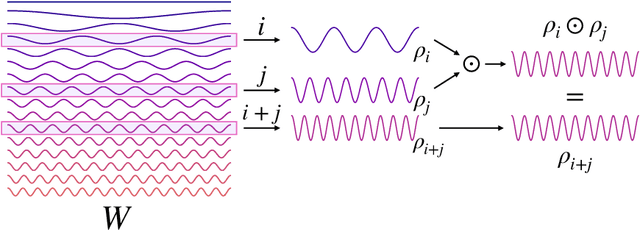
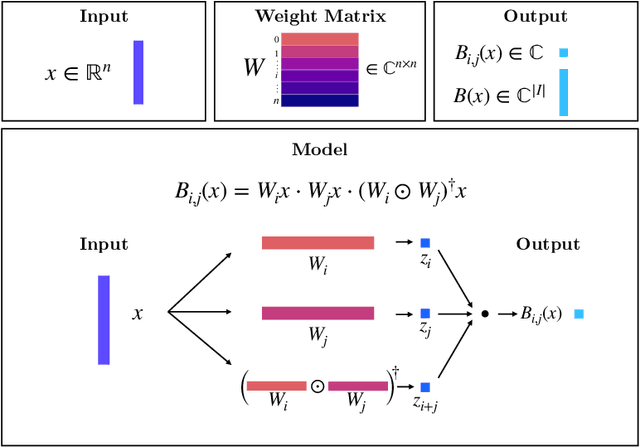
We present a novel machine learning architecture, Bispectral Neural Networks (BNNs), for learning representations of data that are invariant to the actions of groups on the space over which a signal is defined. The model incorporates the ansatz of the bispectrum, an analytically defined group invariant that is complete--that is, it preserves all signal structure while removing only the variation due to group actions. Here, we demonstrate that BNNs are able to discover arbitrary commutative group structure in data, with the trained models learning the irreducible representations of the groups, which allows for the recovery of the group Cayley tables. Remarkably, trained networks learn to approximate bispectra on these groups, and thus possess the robustness, completeness, and generality of the analytical object.

Efficient Neuromorphic Signal Processing with Loihi 2

The biologically inspired spiking neurons used in neuromorphic computing are nonlinear filters with dynamic state variables -- very different from the stateless neuron models used in deep learning. The next version of Intel's neuromorphic research processor, Loihi 2, supports a wide range of stateful spiking neuron models with fully programmable dynamics. Here we showcase advanced spiking neuron models that can be used to efficiently process streaming data in simulation experiments on emulated Loihi 2 hardware. In one example, Resonate-and-Fire (RF) neurons are used to compute the Short Time Fourier Transform (STFT) with similar computational complexity but 47x less output bandwidth than the conventional STFT. In another example, we describe an algorithm for optical flow estimation using spatiotemporal RF neurons that requires over 90x fewer operations than a conventional DNN-based solution. We also demonstrate promising preliminary results using backpropagation to train RF neurons for audio classification tasks. Finally, we show that a cascade of Hopf resonators - a variant of the RF neuron - replicates novel properties of the cochlea and motivates an efficient spike-based spectrogram encoder.