The Complexity of NISQ

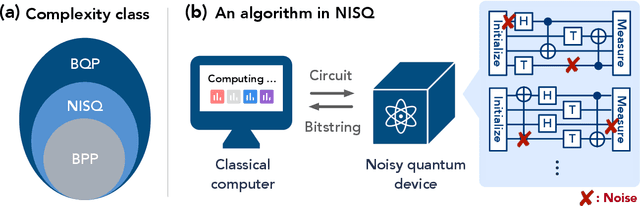
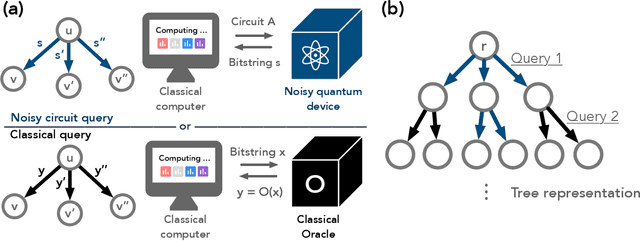
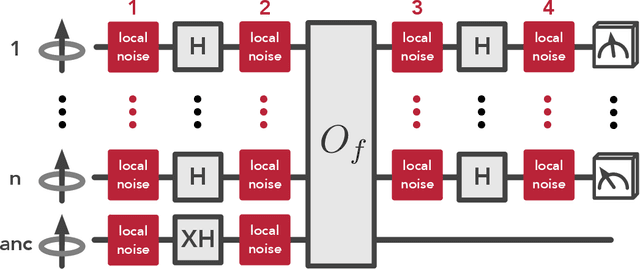
The recent proliferation of NISQ devices has made it imperative to understand their computational power. In this work, we define and study the complexity class $\textsf{NISQ} $, which is intended to encapsulate problems that can be efficiently solved by a classical computer with access to a NISQ device. To model existing devices, we assume the device can (1) noisily initialize all qubits, (2) apply many noisy quantum gates, and (3) perform a noisy measurement on all qubits. We first give evidence that $\textsf{BPP}\subsetneq \textsf{NISQ}\subsetneq \textsf{BQP}$, by demonstrating super-polynomial oracle separations among the three classes, based on modifications of Simon's problem. We then consider the power of $\textsf{NISQ}$ for three well-studied problems. For unstructured search, we prove that $\textsf{NISQ}$ cannot achieve a Grover-like quadratic speedup over $\textsf{BPP}$. For the Bernstein-Vazirani problem, we show that $\textsf{NISQ}$ only needs a number of queries logarithmic in what is required for $\textsf{BPP}$. Finally, for a quantum state learning problem, we prove that $\textsf{NISQ}$ is exponentially weaker than classical computation with access to noiseless constant-depth quantum circuits.

Sampling is as easy as learning the score: theory for diffusion models with minimal data assumptions

We provide theoretical convergence guarantees for score-based generative models (SGMs) such as denoising diffusion probabilistic models (DDPMs), which constitute the backbone of large-scale real-world generative models such as DALL$\cdot$E 2. Our main result is that, assuming accurate score estimates, such SGMs can efficiently sample from essentially any realistic data distribution. In contrast to prior works, our results (1) hold for an $L^2$-accurate score estimate (rather than $L^\infty$-accurate); (2) do not require restrictive functional inequality conditions that preclude substantial non-log-concavity; (3) scale polynomially in all relevant problem parameters; and (4) match state-of-the-art complexity guarantees for discretization of the Langevin diffusion, provided that the score error is sufficiently small. We view this as strong theoretical justification for the empirical success of SGMs. We also examine SGMs based on the critically damped Langevin diffusion (CLD). Contrary to conventional wisdom, we provide evidence that the use of the CLD does not reduce the complexity of SGMs.

Tight Bounds for State Tomography with Incoherent Measurements

We consider the classic question of state tomography: given copies of an unknown quantum state $\rho\in\mathbb{C}^{d\times d}$, output $\widehat{\rho}$ for which $\|\rho - \widehat{\rho}\|_{\mathsf{tr}} \le \varepsilon$. When one is allowed to make coherent measurements entangled across all copies, $\Theta(d^2/\varepsilon^2)$ copies are necessary and sufficient [Haah et al. '17, O'Donnell-Wright '16]. Unfortunately, the protocols achieving this rate incur large quantum memory overheads that preclude implementation on current or near-term devices. On the other hand, the best known protocol using incoherent (single-copy) measurements uses $O(d^3/\varepsilon^2)$ copies [Kueng-Rauhut-Terstiege '17], and multiple papers have posed it as an open question to understand whether or not this rate is tight. In this work, we fully resolve this question, by showing that any protocol using incoherent measurements, even if they are chosen adaptively, requires $\Omega(d^3/\varepsilon^2)$ copies, matching the upper bound of [Kueng-Rauhut-Terstiege '17]. We do so by a new proof technique which directly bounds the "tilt" of the posterior distribution after measurements, which yields a surprisingly short proof of our lower bound, and which we believe may be of independent interest.

Learning (Very) Simple Generative Models Is Hard

Motivated by the recent empirical successes of deep generative models, we study the computational complexity of the following unsupervised learning problem. For an unknown neural network $F:\mathbb{R}^d\to\mathbb{R}^{d'}$, let $D$ be the distribution over $\mathbb{R}^{d'}$ given by pushing the standard Gaussian $\mathcal{N}(0,\textrm{Id}_d)$ through $F$. Given i.i.d. samples from $D$, the goal is to output any distribution close to $D$ in statistical distance. We show under the statistical query (SQ) model that no polynomial-time algorithm can solve this problem even when the output coordinates of $F$ are one-hidden-layer ReLU networks with $\log(d)$ neurons. Previously, the best lower bounds for this problem simply followed from lower bounds for supervised learning and required at least two hidden layers and $\mathrm{poly}(d)$ neurons [Daniely-Vardi '21, Chen-Gollakota-Klivans-Meka '22]. The key ingredient in our proof is an ODE-based construction of a compactly supported, piecewise-linear function $f$ with polynomially-bounded slopes such that the pushforward of $\mathcal{N}(0,1)$ under $f$ matches all low-degree moments of $\mathcal{N}(0,1)$.

Tight Bounds for Quantum State Certification with Incoherent Measurements

We consider the problem of quantum state certification, where we are given the description of a mixed state $\sigma \in \mathbb{C}^{d \times d}$, $n$ copies of a mixed state $\rho \in \mathbb{C}^{d \times d}$, and $\varepsilon > 0$, and we are asked to determine whether $\rho = \sigma$ or whether $\| \rho - \sigma \|_1 > \varepsilon$. When $\sigma$ is the maximally mixed state $\frac{1}{d} I_d$, this is known as mixedness testing. We focus on algorithms which use incoherent measurements, i.e. which only measure one copy of $\rho$ at a time. Unlike those that use entangled, multi-copy measurements, these can be implemented without persistent quantum memory and thus represent a large class of protocols that can be run on current or near-term devices. For mixedness testing, there is a folklore algorithm which uses incoherent measurements and only needs $O(d^{3/2} / \varepsilon^2)$ copies. The algorithm is non-adaptive, that is, its measurements are fixed ahead of time, and is known to be optimal for non-adaptive algorithms. However, when the algorithm can make arbitrary incoherent measurements, the best known lower bound is only $\Omega (d^{4/3} / \varepsilon^2)$ [Bubeck-Chen-Li '20], and it has been an outstanding open problem to close this polynomial gap. In this work, 1) we settle the copy complexity of mixedness testing with incoherent measurements and show that $\Omega (d^{3/2} / \varepsilon^2)$ copies are necessary, and 2) we show the instance-optimal bounds for state certification to general $\sigma$ first derived by [Chen-Li-O'Donnell '21] for non-adaptive measurements also hold for arbitrary incoherent measurements. Qualitatively, our results say that adaptivity does not help at all for these problems. Our results are based on new techniques that allow us to reduce the problem to understanding certain matrix martingales, which we believe may be of independent interest.

Learning Polynomial Transformations

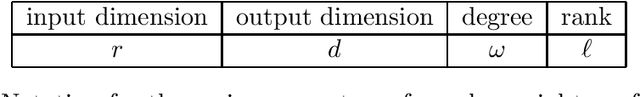
We consider the problem of learning high dimensional polynomial transformations of Gaussians. Given samples of the form $p(x)$, where $x\sim N(0, \mathrm{Id}_r)$ is hidden and $p: \mathbb{R}^r \to \mathbb{R}^d$ is a function where every output coordinate is a low-degree polynomial, the goal is to learn the distribution over $p(x)$. This problem is natural in its own right, but is also an important special case of learning deep generative models, namely pushforwards of Gaussians under two-layer neural networks with polynomial activations. Understanding the learnability of such generative models is crucial to understanding why they perform so well in practice. Our first main result is a polynomial-time algorithm for learning quadratic transformations of Gaussians in a smoothed setting. Our second main result is a polynomial-time algorithm for learning constant-degree polynomial transformations of Gaussian in a smoothed setting, when the rank of the associated tensors is small. In fact our results extend to any rotation-invariant input distribution, not just Gaussian. These are the first end-to-end guarantees for learning a pushforward under a neural network with more than one layer. Along the way, we also give the first polynomial-time algorithms with provable guarantees for tensor ring decomposition, a popular generalization of tensor decomposition that is used in practice to implicitly store large tensors.

Hardness of Noise-Free Learning for Two-Hidden-Layer Neural Networks

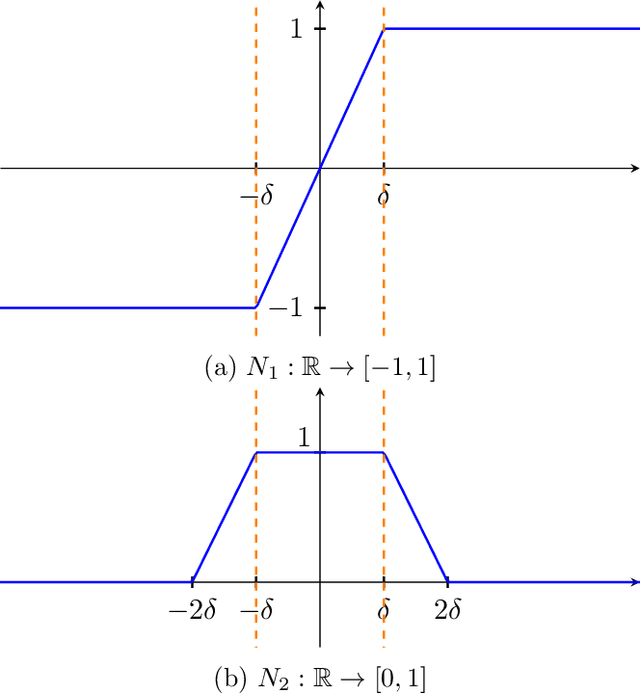
We give exponential statistical query (SQ) lower bounds for learning two-hidden-layer ReLU networks with respect to Gaussian inputs in the standard (noise-free) model. No general SQ lower bounds were known for learning ReLU networks of any depth in this setting: previous SQ lower bounds held only for adversarial noise models (agnostic learning) or restricted models such as correlational SQ. Prior work hinted at the impossibility of our result: Vempala and Wilmes showed that general SQ lower bounds cannot apply to any real-valued family of functions that satisfies a simple non-degeneracy condition. To circumvent their result, we refine a lifting procedure due to Daniely and Vardi that reduces Boolean PAC learning problems to Gaussian ones. We show how to extend their technique to other learning models and, in many well-studied cases, obtain a more efficient reduction. As such, we also prove new cryptographic hardness results for PAC learning two-hidden-layer ReLU networks, as well as new lower bounds for learning constant-depth ReLU networks from membership queries.

Minimax Optimality (Probably) Doesn't Imply Distribution Learning for GANs

Arguably the most fundamental question in the theory of generative adversarial networks (GANs) is to understand to what extent GANs can actually learn the underlying distribution. Theoretical and empirical evidence suggests local optimality of the empirical training objective is insufficient. Yet, it does not rule out the possibility that achieving a true population minimax optimal solution might imply distribution learning. In this paper, we show that standard cryptographic assumptions imply that this stronger condition is still insufficient. Namely, we show that if local pseudorandom generators (PRGs) exist, then for a large family of natural continuous target distributions, there are ReLU network generators of constant depth and polynomial size which take Gaussian random seeds so that (i) the output is far in Wasserstein distance from the target distribution, but (ii) no polynomially large Lipschitz discriminator ReLU network can detect this. This implies that even achieving a population minimax optimal solution to the Wasserstein GAN objective is likely insufficient for distribution learning in the usual statistical sense. Our techniques reveal a deep connection between GANs and PRGs, which we believe will lead to further insights into the computational landscape of GANs.

Quantum advantage in learning from experiments

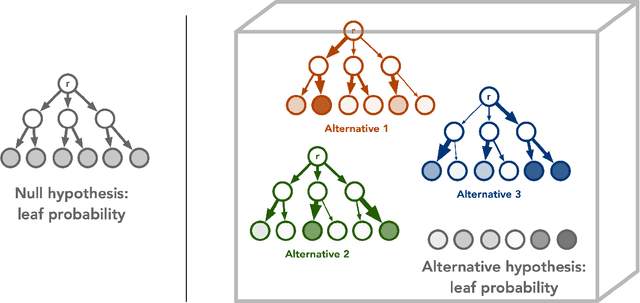
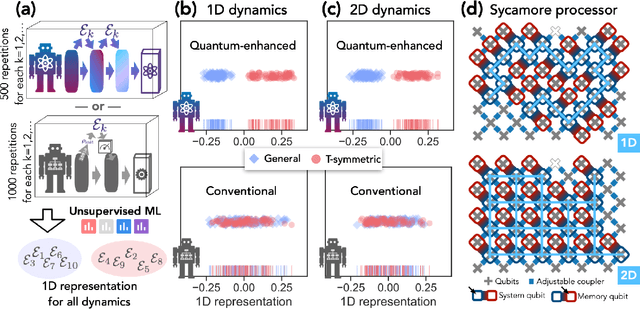
Quantum technology has the potential to revolutionize how we acquire and process experimental data to learn about the physical world. An experimental setup that transduces data from a physical system to a stable quantum memory, and processes that data using a quantum computer, could have significant advantages over conventional experiments in which the physical system is measured and the outcomes are processed using a classical computer. We prove that, in various tasks, quantum machines can learn from exponentially fewer experiments than those required in conventional experiments. The exponential advantage holds in predicting properties of physical systems, performing quantum principal component analysis on noisy states, and learning approximate models of physical dynamics. In some tasks, the quantum processing needed to achieve the exponential advantage can be modest; for example, one can simultaneously learn about many noncommuting observables by processing only two copies of the system. Conducting experiments with up to 40 superconducting qubits and 1300 quantum gates, we demonstrate that a substantial quantum advantage can be realized using today's relatively noisy quantum processors. Our results highlight how quantum technology can enable powerful new strategies to learn about nature.

Exponential separations between learning with and without quantum memory

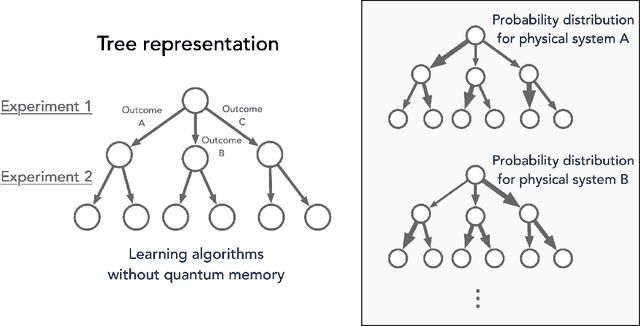
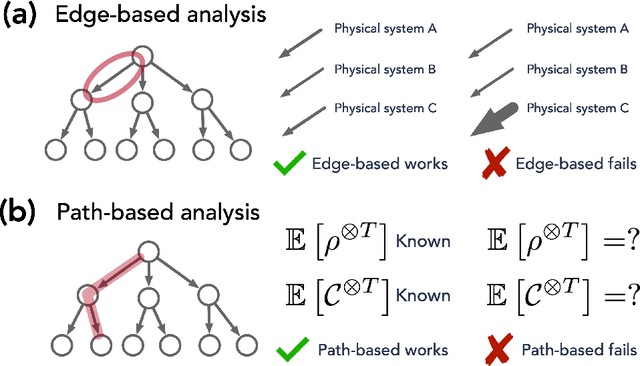
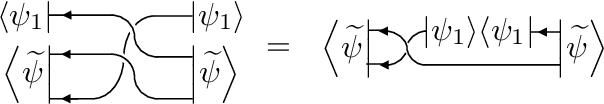
We study the power of quantum memory for learning properties of quantum systems and dynamics, which is of great importance in physics and chemistry. Many state-of-the-art learning algorithms require access to an additional external quantum memory. While such a quantum memory is not required a priori, in many cases, algorithms that do not utilize quantum memory require much more data than those which do. We show that this trade-off is inherent in a wide range of learning problems. Our results include the following: (1) We show that to perform shadow tomography on an $n$-qubit state rho with $M$ observables, any algorithm without quantum memory requires $\Omega(\min(M, 2^n))$ samples of rho in the worst case. Up to logarithmic factors, this matches the upper bound of [HKP20] and completely resolves an open question in [Aar18, AR19]. (2) We establish exponential separations between algorithms with and without quantum memory for purity testing, distinguishing scrambling and depolarizing evolutions, as well as uncovering symmetry in physical dynamics. Our separations improve and generalize prior work of [ACQ21] by allowing for a broader class of algorithms without quantum memory. (3) We give the first tradeoff between quantum memory and sample complexity. We prove that to estimate absolute values of all $n$-qubit Pauli observables, algorithms with $k < n$ qubits of quantum memory require at least $\Omega(2^{(n-k)/3})$ samples, but there is an algorithm using $n$-qubit quantum memory which only requires $O(n)$ samples. The separations we show are sufficiently large and could already be evident, for instance, with tens of qubits. This provides a concrete path towards demonstrating real-world advantage for learning algorithms with quantum memory.