Implicit Regularization of Discrete Gradient Dynamics in Deep Linear Neural Networks

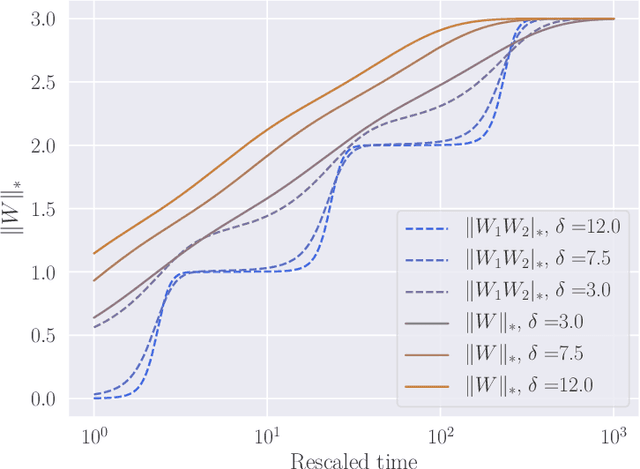
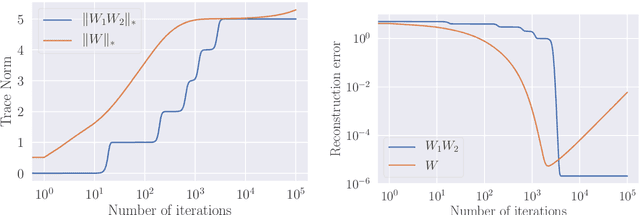
When optimizing over-parameterized models, such as deep neural networks, a large set of parameters can achieve zero training error. In such cases, the choice of the optimization algorithm and its respective hyper-parameters introduces biases that will lead to convergence to specific minimizers of the objective. Consequently, this choice can be considered as an implicit regularization for the training of over-parametrized models. In this work, we push this idea further by studying the discrete gradient dynamics of the training of a two-layer linear network with the least-square loss. Using a time rescaling, we show that, with a vanishing initialization and a small enough step size, this dynamics sequentially learns components that are the solutions of a reduced-rank regression with a gradually increasing rank.

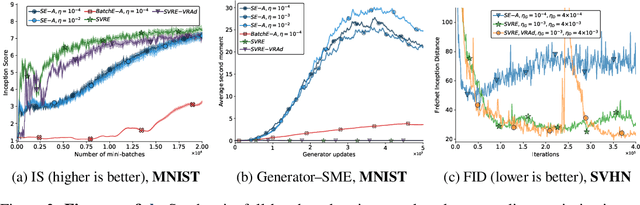
Reducing Noise in GAN Training with Variance Reduced Extragradient

Using large mini-batches when training generative adversarial networks (GANs) has been recently shown to significantly improve the quality of the generated samples. This can be seen as a simple but computationally expensive way of reducing the noise of the gradient estimates. In this paper, we investigate the effect of the noise in this context and show that it can prevent the convergence of standard stochastic game optimization methods, while their respective batch version converges. To address this issue, we propose a variance-reduced version of the stochastic extragradient algorithm (SVRE). We show experimentally that it performs similarly to a batch method, while being computationally cheaper, and show its theoretical convergence, improving upon the best rates proposed in the literature. Experiments on several datasets show that SVRE improves over baselines. Notably, SVRE is the first optimization method for GANs to our knowledge that can produce near state-of-the-art results without using adaptive step-size such as Adam.

Centroid Networks for Few-Shot Clustering and Unsupervised Few-Shot Classification

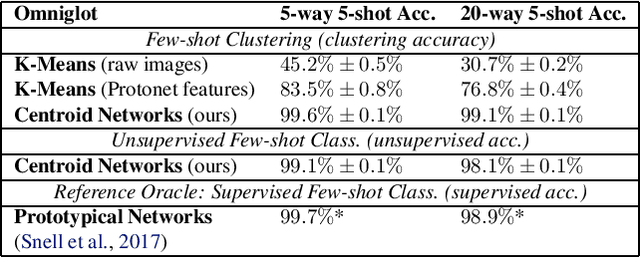
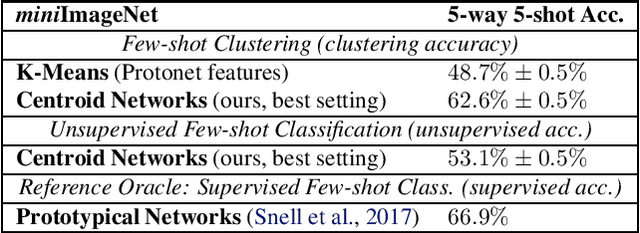
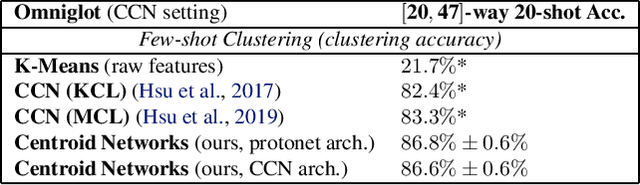
Traditional clustering algorithms such as K-means rely heavily on the nature of the chosen metric or data representation. To get meaningful clusters, these representations need to be tailored to the downstream task (e.g. cluster photos by object category, cluster faces by identity). Therefore, we frame clustering as a meta-learning task, few-shot clustering, which allows us to specify how to cluster the data at the meta-training level, despite the clustering algorithm itself being unsupervised. We propose Centroid Networks, a simple and efficient few-shot clustering method based on learning representations which are tailored both to the task to solve and to its internal clustering module. We also introduce unsupervised few-shot classification, which is conceptually similar to few-shot clustering, but is strictly harder than supervised* few-shot classification and therefore allows direct comparison with existing supervised few-shot classification methods. On Omniglot and miniImageNet, our method achieves accuracy competitive with popular supervised few-shot classification algorithms, despite using *no labels* from the support set. We also show performance competitive with state-of-the-art learning-to-cluster methods.

Predicting Tactical Solutions to Operational Planning Problems under Imperfect Information

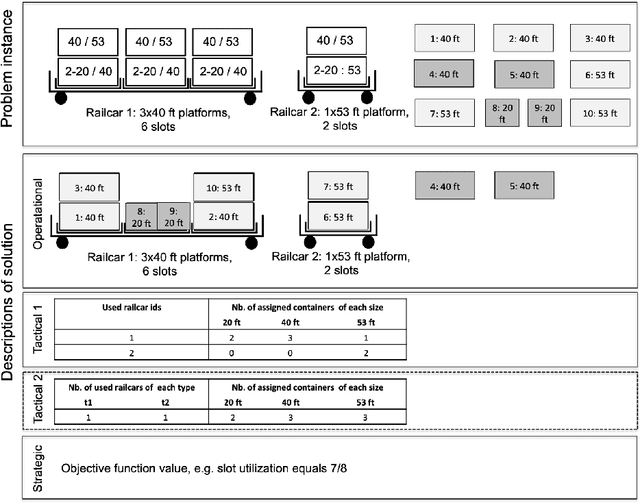
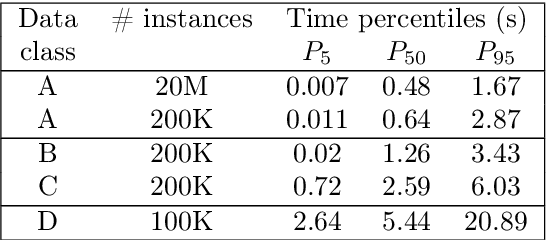
This paper offers a methodological contribution at the intersection of machine learning and operations research. Namely, we propose a methodology to quickly predict tactical solutions to a given operational problem. In this context, the tactical solution is less detailed than the operational one but it has to be computed in very short time and under imperfect information. The problem is of importance in various applications where tactical and operational planning problems are interrelated and information about the operational problem is revealed over time. This is for instance the case in certain capacity planning and demand management systems. We formulate the problem as a two-stage optimal prediction stochastic program whose solution we predict with a supervised machine learning algorithm. The training data set consists of a large number of deterministic (second stage) problems generated by controlled probabilistic sampling. The labels are computed based on solutions to the deterministic problems (solved independently and offline) employing appropriate aggregation and subselection methods to address uncertainty. Results on our motivating application in load planning for rail transportation show that deep learning algorithms produce highly accurate predictions in very short computing time (milliseconds or less). The prediction accuracy is comparable to solutions computed by sample average approximation of the stochastic program.

A Variational Inequality Perspective on Generative Adversarial Networks

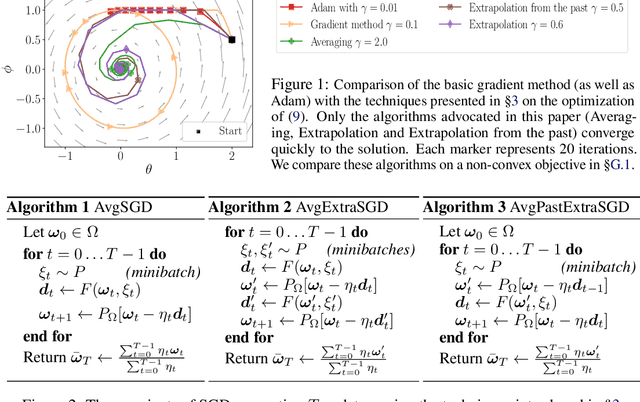
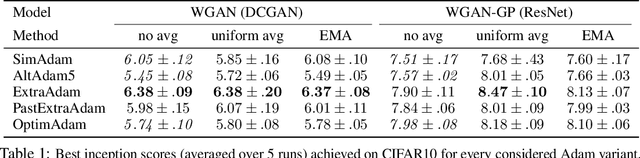
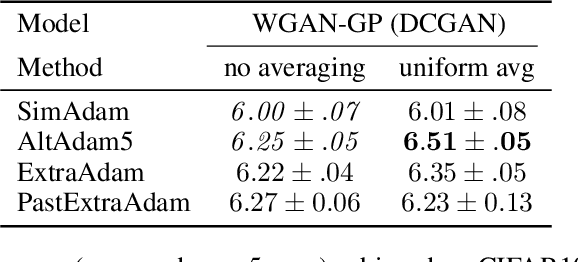
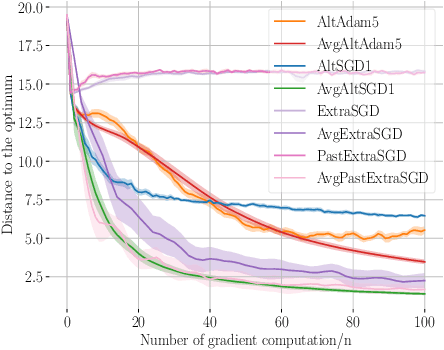
Generative adversarial networks (GANs) form a generative modeling approach known for producing appealing samples, but they are notably difficult to train. One common way to tackle this issue has been to propose new formulations of the GAN objective. Yet, surprisingly few studies have looked at optimization methods designed for this adversarial training. In this work, we cast GAN optimization problems in the general variational inequality framework. Tapping into the mathematical programming literature, we counter some common misconceptions about the difficulties of saddle point optimization and propose to extend techniques designed for variational inequalities to the training of GANs. We apply averaging, extrapolation and a novel computationally cheaper variant that we call extrapolation from the past to the stochastic gradient method (SGD) and Adam.

Quantifying Learning Guarantees for Convex but Inconsistent Surrogates

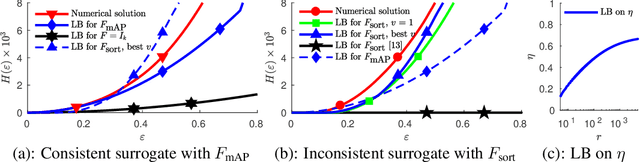
We study consistency properties of machine learning methods based on minimizing convex surrogates. We extend the recent framework of Osokin et al. (2017) for the quantitative analysis of consistency properties to the case of inconsistent surrogates. Our key technical contribution consists in a new lower bound on the calibration function for the quadratic surrogate, which is non-trivial (not always zero) for inconsistent cases. The new bound allows to quantify the level of inconsistency of the setting and shows how learning with inconsistent surrogates can have guarantees on sample complexity and optimization difficulty. We apply our theory to two concrete cases: multi-class classification with the tree-structured loss and ranking with the mean average precision loss. The results show the approximation-computation trade-offs caused by inconsistent surrogates and their potential benefits.

A Modern Take on the Bias-Variance Tradeoff in Neural Networks

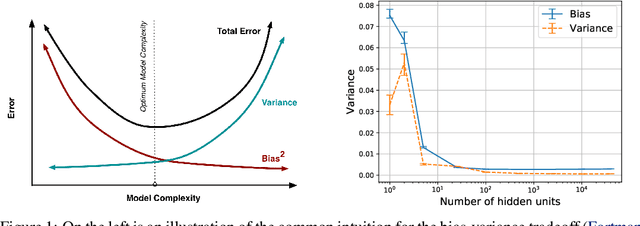
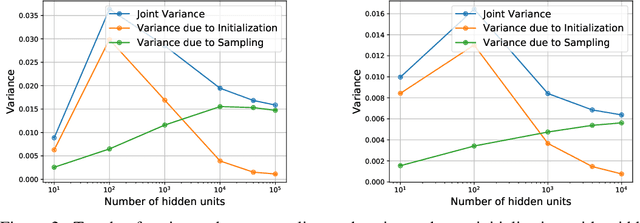
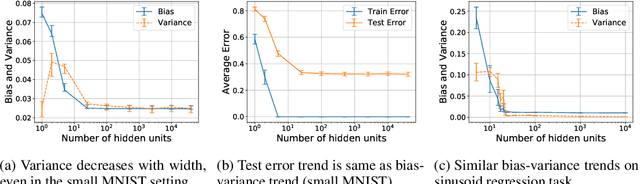
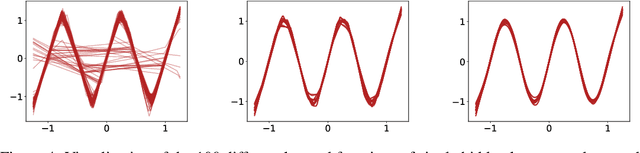
We revisit the bias-variance tradeoff for neural networks in light of modern empirical findings. The traditional bias-variance tradeoff in machine learning suggests that as model complexity grows, variance increases. Classical bounds in statistical learning theory point to the number of parameters in a model as a measure of model complexity, which means the tradeoff would indicate that variance increases with the size of neural networks. However, we empirically find that variance due to training set sampling is roughly \textit{constant} (with both width and depth) in practice. Variance caused by the non-convexity of the loss landscape is different. We find that it decreases with width and increases with depth, in our setting. We provide theoretical analysis, in a simplified setting inspired by linear models, that is consistent with our empirical findings for width. We view bias-variance as a useful lens to study generalization through and encourage further theoretical explanation from this perspective.

Scattering Networks for Hybrid Representation Learning

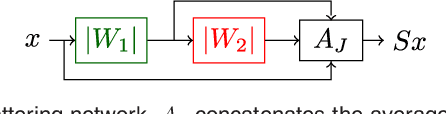
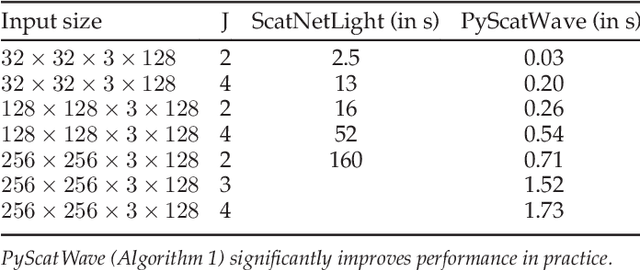
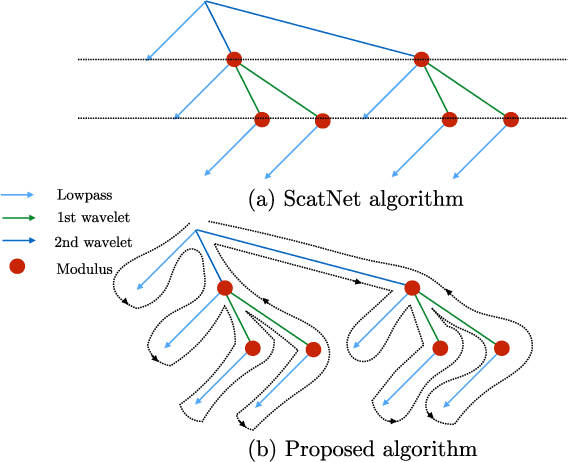
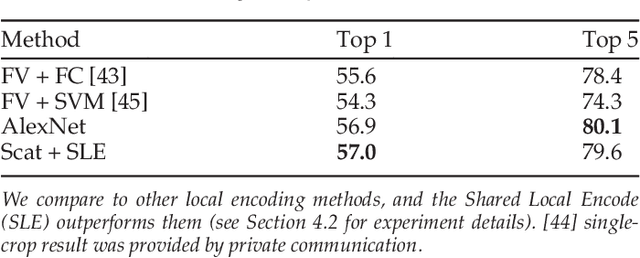
Scattering networks are a class of designed Convolutional Neural Networks (CNNs) with fixed weights. We argue they can serve as generic representations for modelling images. In particular, by working in scattering space, we achieve competitive results both for supervised and unsupervised learning tasks, while making progress towards constructing more interpretable CNNs. For supervised learning, we demonstrate that the early layers of CNNs do not necessarily need to be learned, and can be replaced with a scattering network instead. Indeed, using hybrid architectures, we achieve the best results with predefined representations to-date, while being competitive with end-to-end learned CNNs. Specifically, even applying a shallow cascade of small-windowed scattering coefficients followed by 1$\times$1-convolutions results in AlexNet accuracy on the ILSVRC2012 classification task. Moreover, by combining scattering networks with deep residual networks, we achieve a single-crop top-5 error of 11.4% on ILSVRC2012. Also, we show they can yield excellent performance in the small sample regime on CIFAR-10 and STL-10 datasets, exceeding their end-to-end counterparts, through their ability to incorporate geometrical priors. For unsupervised learning, scattering coefficients can be a competitive representation that permits image recovery. We use this fact to train hybrid GANs to generate images. Finally, we empirically analyze several properties related to stability and reconstruction of images from scattering coefficients.

Predicting Solution Summaries to Integer Linear Programs under Imperfect Information with Machine Learning

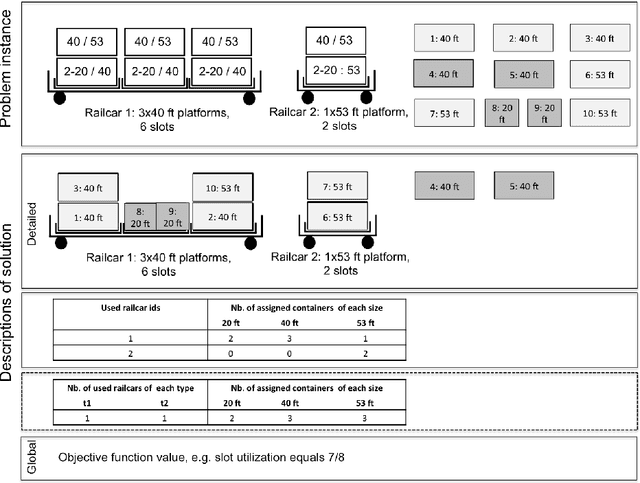
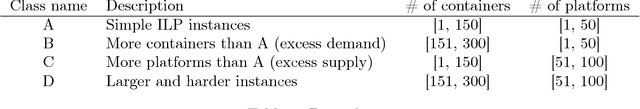
The paper provides a methodological contribution at the intersection of machine learning and operations research. Namely, we propose a methodology to quickly predict solution summaries (i.e., solution descriptions at a given level of detail) to discrete stochastic optimization problems. We approximate the solutions based on supervised learning and the training dataset consists of a large number of deterministic problems that have been solved independently and offline. Uncertainty regarding a missing subset of the inputs is addressed through sampling and aggregation methods. Our motivating application concerns booking decisions of intermodal containers on double-stack trains. Under perfect information, this is the so-called load planning problem and it can be formulated by means of integer linear programming. However, the formulation cannot be used for the application at hand because of the restricted computational budget and unknown container weights. The results show that standard deep learning algorithms allow one to predict descriptions of solutions with high accuracy in very short time (milliseconds or less).

Negative Momentum for Improved Game Dynamics

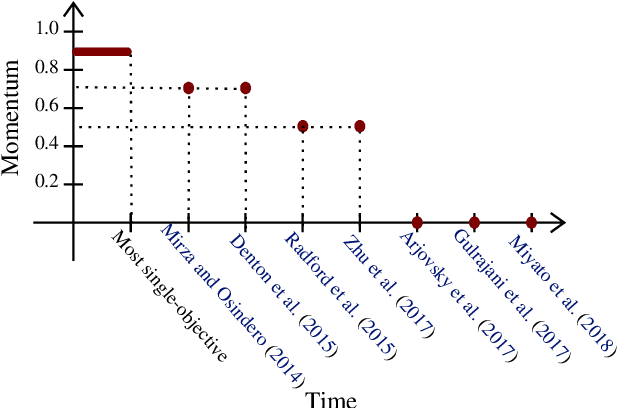
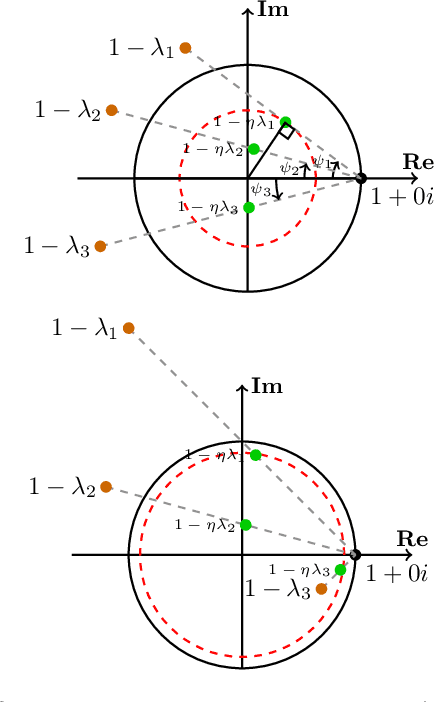
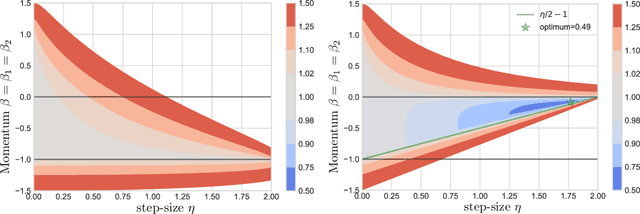
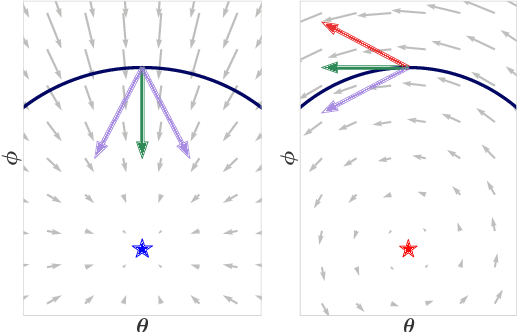
Games generalize the optimization paradigm by introducing different objective functions for different optimizing agents, known as players. Generative Adversarial Networks (GANs) are arguably the most popular game formulation in recent machine learning literature. GANs achieve great results on generating realistic natural images, however they are known for being difficult to train. Training them involves finding a Nash equilibrium, typically performed using gradient descent on the two players' objectives. Game dynamics can induce rotations that slow down convergence to a Nash equilibrium, or prevent it altogether. We provide a theoretical analysis of the game dynamics. Our analysis, supported by experiments, shows that gradient descent with a negative momentum term can improve the convergence properties of some GANs.