To Each Optimizer a Norm, To Each Norm its Generalization

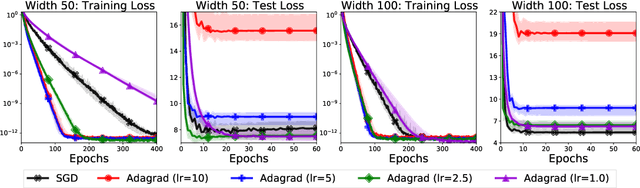
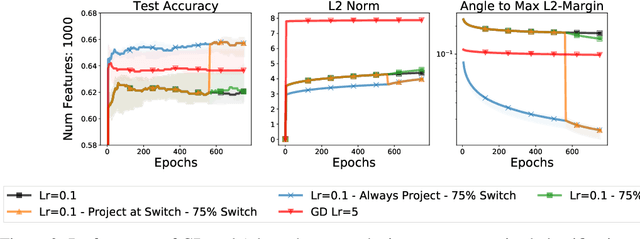
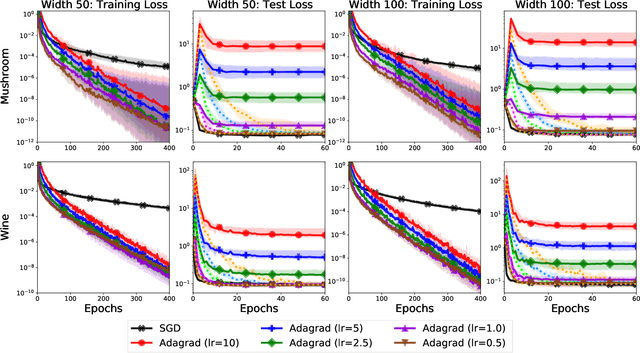
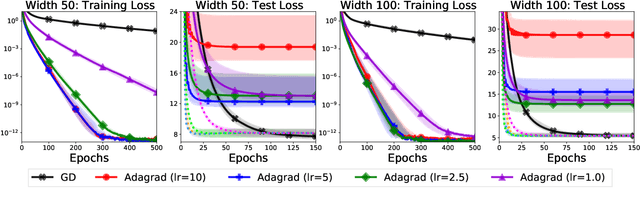
We study the implicit regularization of optimization methods for linear models interpolating the training data in the under-parametrized and over-parametrized regimes. Since it is difficult to determine whether an optimizer converges to solutions that minimize a known norm, we flip the problem and investigate what is the corresponding norm minimized by an interpolating solution. Using this reasoning, we prove that for over-parameterized linear regression, projections onto linear spans can be used to move between different interpolating solutions. For under-parameterized linear classification, we prove that for any linear classifier separating the data, there exists a family of quadratic norms ||.||_P such that the classifier's direction is the same as that of the maximum P-margin solution. For linear classification, we argue that analyzing convergence to the standard maximum l2-margin is arbitrary and show that minimizing the norm induced by the data results in better generalization. Furthermore, for over-parameterized linear classification, projections onto the data-span enable us to use techniques from the under-parameterized setting. On the empirical side, we propose techniques to bias optimizers towards better generalizing solutions, improving their test performance. We validate our theoretical results via synthetic experiments, and use the neural tangent kernel to handle non-linear models.

An Analysis of the Adaptation Speed of Causal Models

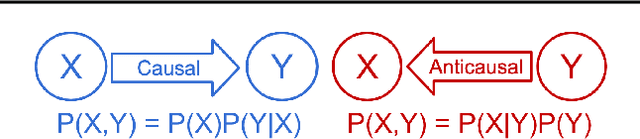
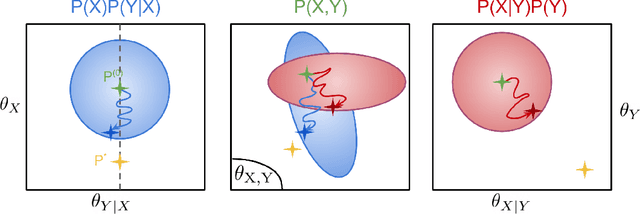
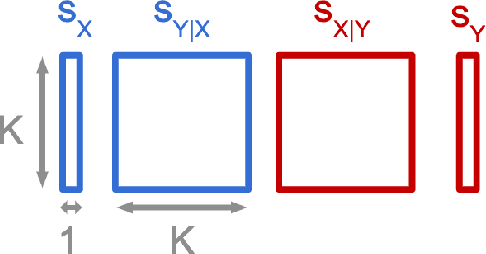
We consider the problem of discovering the causal process that generated a collection of datasets. We assume that all these datasets were generated by unknown sparse interventions on a structural causal model (SCM) $G$, that we want to identify. Recently, Bengio et al. (2020) argued that among all SCMs, $G$ is the fastest to adapt from one dataset to another, and proposed a meta-learning criterion to identify the causal direction in a two-variable SCM. While the experiments were promising, the theoretical justification was incomplete. Our contribution is a theoretical investigation of the adaptation speed of simple two-variable SCMs. We use convergence rates from stochastic optimization to justify that a relevant proxy for adaptation speed is distance in parameter space after intervention. Using this proxy, we show that the SCM with the correct causal direction is advantaged for categorical and normal cause-effect datasets when the intervention is on the cause variable. When the intervention is on the effect variable, we provide a more nuanced picture which highlights that the fastest-to-adapt heuristic is not always valid. Code to reproduce experiments is available at https://github.com/remilepriol/causal-adaptation-speed

Stochastic Polyak Step-size for SGD: An Adaptive Learning Rate for Fast Convergence

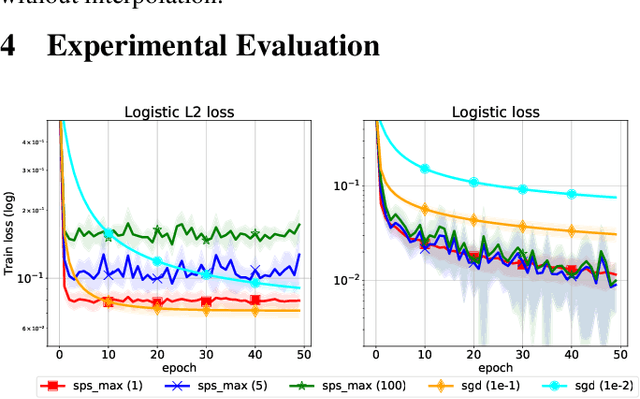
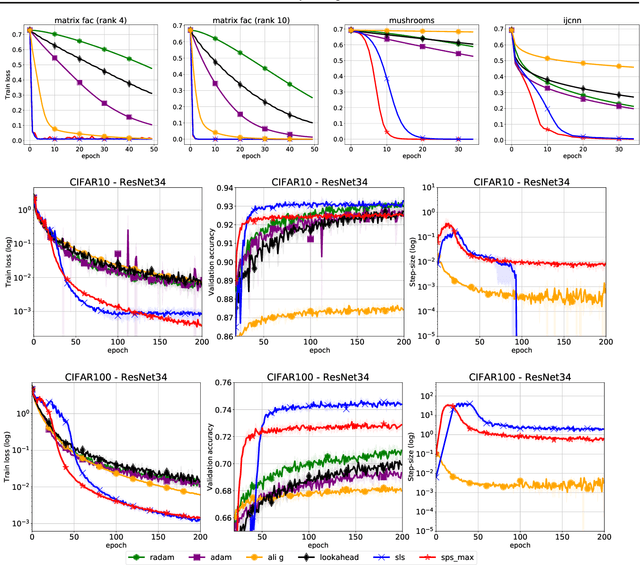
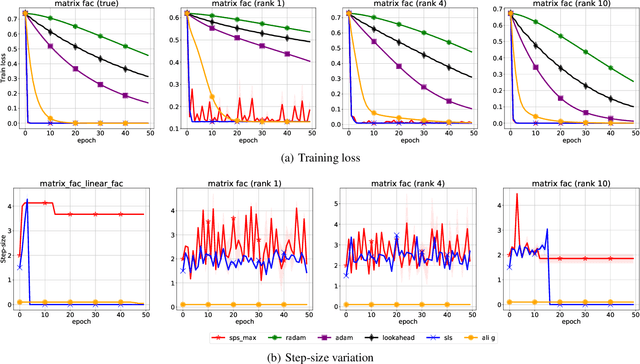
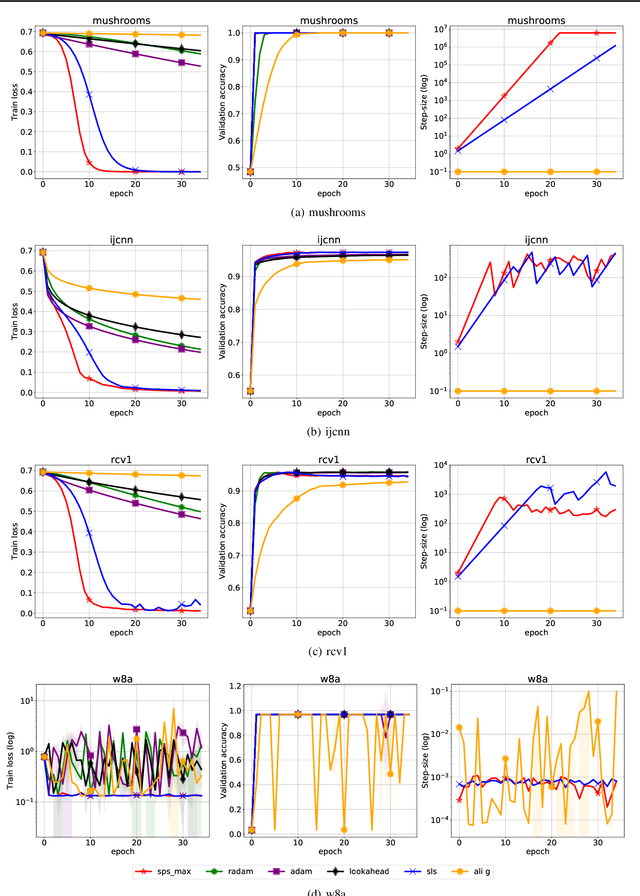
We propose a stochastic variant of the classical Polyak step-size (Polyak, 1987) commonly used in the subgradient method. Although computing the Polyak step-size requires knowledge of the optimal function values, this information is readily available for typical modern machine learning applications. Consequently, the proposed stochastic Polyak step-size (SPS) is an attractive choice for setting the learning rate for stochastic gradient descent (SGD). We provide theoretical convergence guarantees for SGD equipped with SPS in different settings, including strongly convex, convex and non-convex functions. Furthermore, our analysis results in novel convergence guarantees for SGD with a constant step-size. We show that SPS is particularly effective when training over-parameterized models capable of interpolating the training data. In this setting, we prove that SPS enables SGD to converge to the true solution at a fast rate without requiring the knowledge of any problem-dependent constants or additional computational overhead. We experimentally validate our theoretical results via extensive experiments on synthetic and real datasets. We demonstrate the strong performance of SGD with SPS compared to state-of-the-art optimization methods when training over-parameterized models.

Accelerating Smooth Games by Manipulating Spectral Shapes

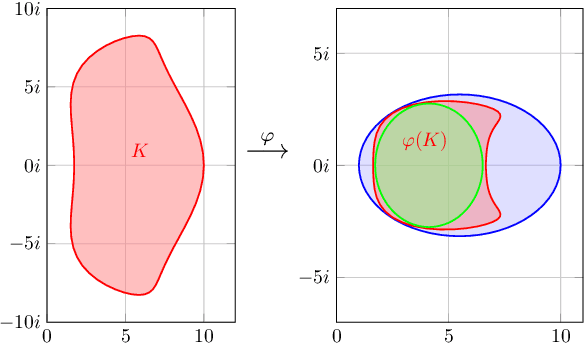
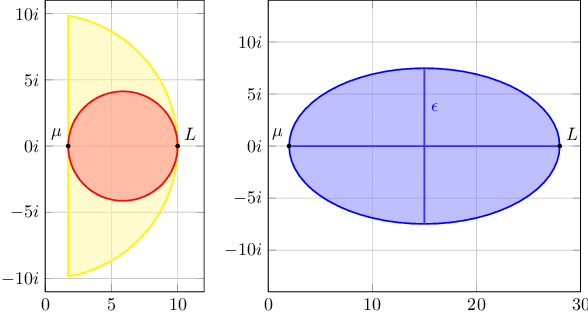
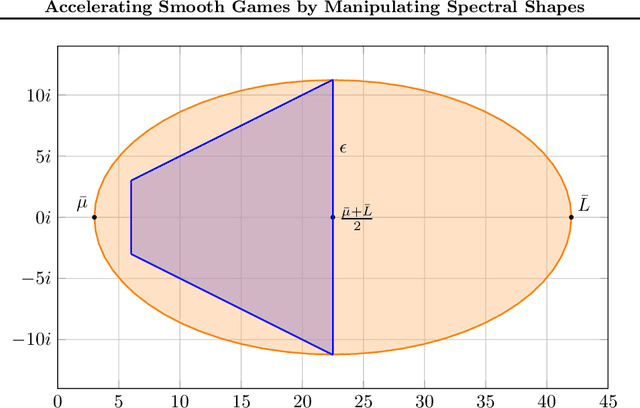
We use matrix iteration theory to characterize acceleration in smooth games. We define the spectral shape of a family of games as the set containing all eigenvalues of the Jacobians of standard gradient dynamics in the family. Shapes restricted to the real line represent well-understood classes of problems, like minimization. Shapes spanning the complex plane capture the added numerical challenges in solving smooth games. In this framework, we describe gradient-based methods, such as extragradient, as transformations on the spectral shape. Using this perspective, we propose an optimal algorithm for bilinear games. For smooth and strongly monotone operators, we identify a continuum between convex minimization, where acceleration is possible using Polyak's momentum, and the worst case where gradient descent is optimal. Finally, going beyond first-order methods, we propose an accelerated version of consensus optimization.

Fast and Furious Convergence: Stochastic Second Order Methods under Interpolation

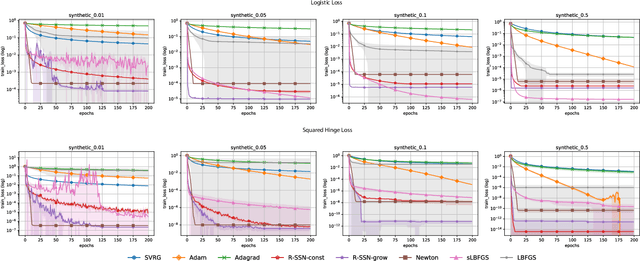
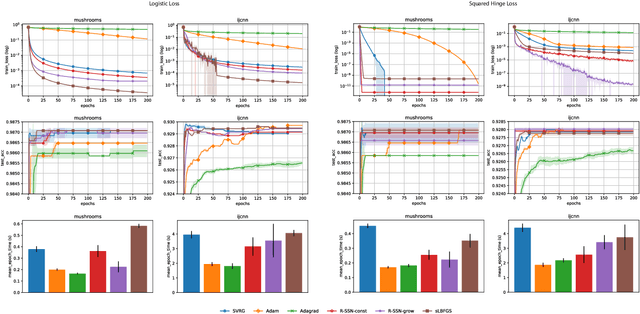
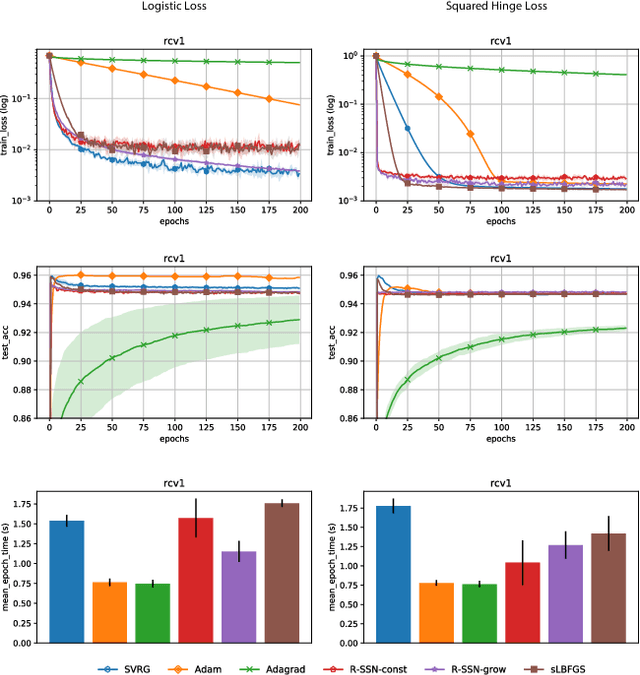
We consider stochastic second order methods for minimizing strongly-convex functions under an interpolation condition satisfied by over-parameterized models. Under this condition, we show that the regularized sub-sampled Newton method (R-SSN) achieves global linear convergence with an adaptive step size and a constant batch size. By growing the batch size for both the sub-sampled gradient and Hessian, we show that R-SSN can converge at a quadratic rate in a local neighbourhood of the solution. We also show that R-SSN attains local linear convergence for the family of self-concordant functions. Furthermore, we analyse stochastic BFGS algorithms in the interpolation setting and prove their global linear convergence. We empirically evaluate stochastic L-BFGS and a "Hessian-free" implementation of R-SSN for binary classification on synthetic, linearly-separable datasets and consider real medium-size datasets under a kernel mapping. Our experimental results show the fast convergence of these methods both in terms of the number of iterations and wall-clock time.

A Tight and Unified Analysis of Extragradient for a Whole Spectrum of Differentiable Games

We consider differentiable games: multi-objective minimization problems, where the goal is to find a Nash equilibrium. The machine learning community has recently started using extrapolation-based variants of the gradient method. A prime example is the extragradient, which yields linear convergence in cases like bilinear games, where the standard gradient method fails. The full benefits of extrapolation-based methods are not known: i) there is no unified analysis for a large class of games that includes both strongly monotone and bilinear games; ii) it is not known whether the rate achieved by extragradient can be improved, e.g. by considering multiple extrapolation steps. We answer these questions through new analysis of the extragradient's local and global convergence properties. Our analysis covers the whole range of settings between purely bilinear and strongly monotone games. It reveals that extragradient converges via different mechanisms at these extremes; in between, it exploits the most favorable mechanism for the given problem. We then present lower bounds on the rate of convergence for a wide class of algorithms with any number of extrapolations. Our bounds prove that the extragradient achieves the optimal rate in this class, and that our upper bounds are tight. Our precise characterization of the extragradient's convergence behavior in games shows that, unlike in convex optimization, the extragradient method may be much faster than the gradient method.

GEAR: Geometry-Aware Rényi Information

Shannon's seminal theory of information has been of paramount importance in the development of modern machine learning techniques. However, standard information measures deal with probability distributions over an alphabet considered as a mere set of symbols and disregard further geometric structure, which might be available in the form of a metric or similarity function. We advocate the use of a notion of entropy that reflects not only the relative abundances of symbols but also the similarities between them, which was originally introduced in theoretical ecology to study the diversity of biological communities. Echoing this idea, we propose a criterion for comparing two probability distributions (possibly degenerate and with non-overlapping supports) that takes into account the geometry of the space in which the distributions are defined. Our proposal exhibits performance on par with state-of-the-art methods based on entropy-regularized optimal transport, but enjoys a closed-form expression and thus a lower computational cost. We demonstrate the versatility of our proposal via experiments on a broad range of domains: computing image barycenters, approximating densities with a collection of (super-) samples; summarizing texts; assessing mode coverage; as well as training generative models.

A Closer Look at the Optimization Landscapes of Generative Adversarial Networks

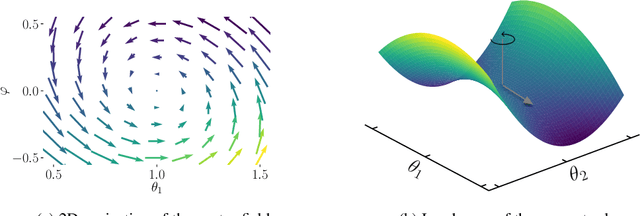
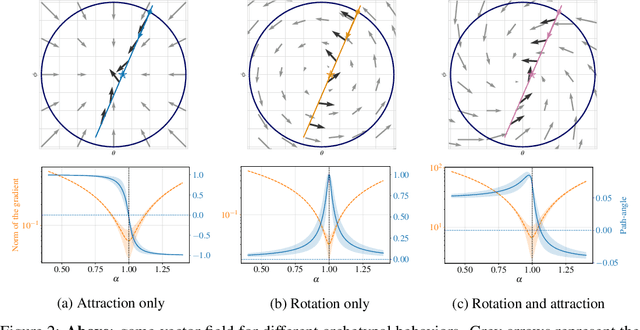
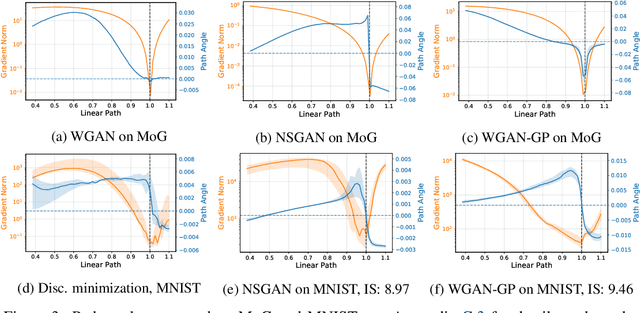
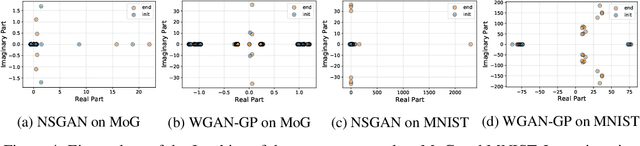
Generative adversarial networks have been very successful in generative modeling, however they remain relatively hard to optimize compared to standard deep neural networks. In this paper, we try to gain insight into the optimization of GANs by looking at the game vector field resulting from the concatenation of the gradient of both players. Based on this point of view, we propose visualization techniques that allow us to make the following empirical observations. First, the training of GANs suffers from rotational behavior around locally stable stationary points, which, as we show, corresponds to the presence of imaginary components in the eigenvalues of the Jacobian of the game. Secondly, GAN training seems to converge to a stable stationary point which is a saddle point for the generator loss, not a minimum, while still achieving excellent performance. This counter-intuitive yet persistent observation questions whether we actually need a Nash equilibrium to get good performance in GANs.

Gradient-Based Neural DAG Learning

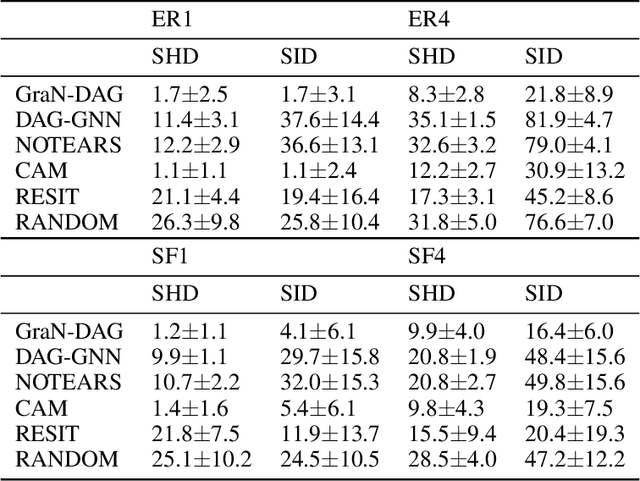
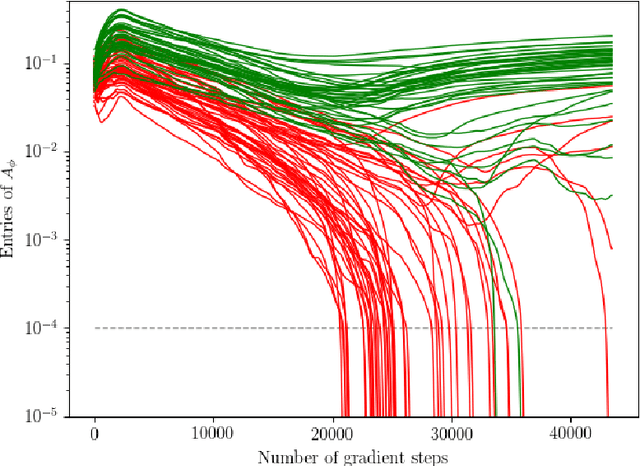
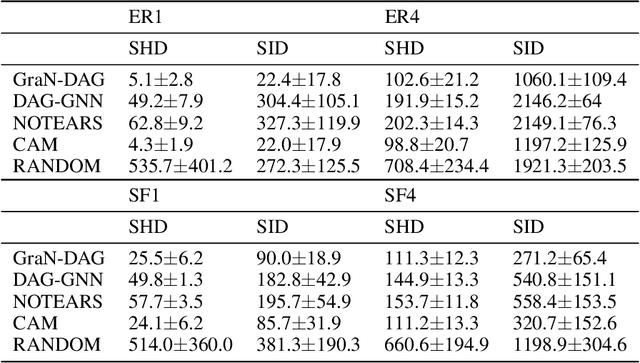
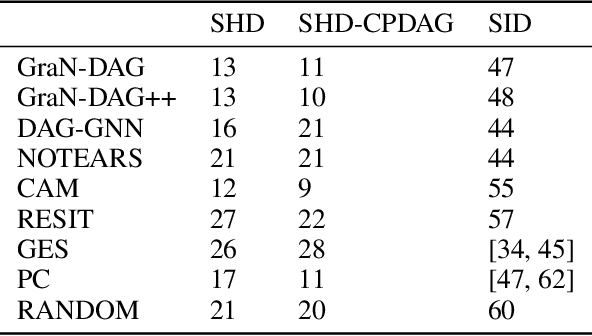
We propose a novel score-based approach to learning a directed acyclic graph (DAG) from observational data. We adapt a recently proposed continuous constrained optimization formulation to allow for nonlinear relationships between variables using neural networks. This extension allows to model complex interactions while being more global in its search compared to other greedy approaches. In addition to comparing our method to existing continuous optimization methods, we provide missing empirical comparisons to nonlinear greedy search methods. On both synthetic and real-world data sets, this new method outperforms current continuous methods on most tasks while being competitive with existing greedy search methods on important metrics for causal inference.

Painless Stochastic Gradient: Interpolation, Line-Search, and Convergence Rates

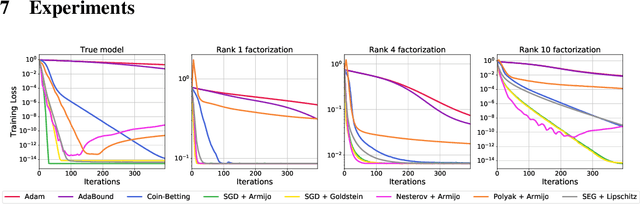
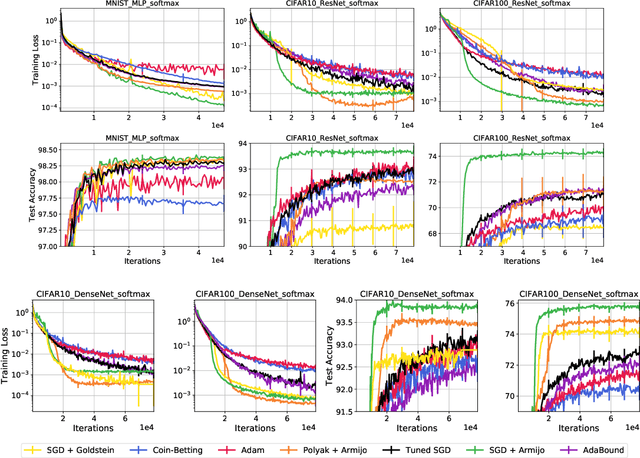
Recent works have shown that stochastic gradient descent (SGD) achieves the fast convergence rates of full-batch gradient descent for over-parameterized models satisfying certain interpolation conditions. However, the step-size used in these works depends on unknown quantities, and SGD's practical performance heavily relies on the choice of the step-size. We propose to use line-search methods to automatically set the step-size when training models that can interpolate the data. We prove that SGD with the classic Armijo line-search attains the fast convergence rates of full-batch gradient descent in convex and strongly-convex settings. We also show that under additional assumptions, SGD with a modified line-search can attain a fast rate of convergence for non-convex functions. Furthermore, we show that a stochastic extra-gradient method with a Lipschitz line-search attains a fast convergence rate for an important class of non-convex functions and saddle-point problems satisfying interpolation. We then give heuristics to use larger step-sizes and acceleration with our line-search techniques. We compare the proposed algorithms against numerous optimization methods for standard classification tasks using both kernel methods and deep networks. The proposed methods are robust and result in competitive performance across all models and datasets. Moreover, for the deep network models, SGD with our line-search results in both faster convergence and better generalization.