Painless Stochastic Gradient: Interpolation, Line-Search, and Convergence Rates

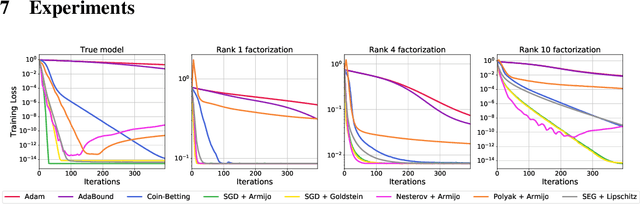
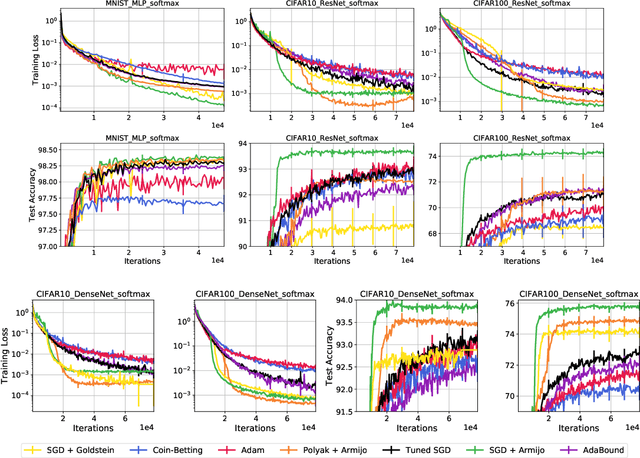
Recent works have shown that stochastic gradient descent (SGD) achieves the fast convergence rates of full-batch gradient descent for over-parameterized models satisfying certain interpolation conditions. However, the step-size used in these works depends on unknown quantities, and SGD's practical performance heavily relies on the choice of the step-size. We propose to use line-search methods to automatically set the step-size when training models that can interpolate the data. We prove that SGD with the classic Armijo line-search attains the fast convergence rates of full-batch gradient descent in convex and strongly-convex settings. We also show that under additional assumptions, SGD with a modified line-search can attain a fast rate of convergence for non-convex functions. Furthermore, we show that a stochastic extra-gradient method with a Lipschitz line-search attains a fast convergence rate for an important class of non-convex functions and saddle-point problems satisfying interpolation. We then give heuristics to use larger step-sizes and acceleration with our line-search techniques. We compare the proposed algorithms against numerous optimization methods for standard classification tasks using both kernel methods and deep networks. The proposed methods are robust and result in competitive performance across all models and datasets. Moreover, for the deep network models, SGD with our line-search results in both faster convergence and better generalization.