CLR: Channel-wise Lightweight Reprogramming for Continual Learning

Continual learning aims to emulate the human ability to continually accumulate knowledge over sequential tasks. The main challenge is to maintain performance on previously learned tasks after learning new tasks, i.e., to avoid catastrophic forgetting. We propose a Channel-wise Lightweight Reprogramming (CLR) approach that helps convolutional neural networks (CNNs) overcome catastrophic forgetting during continual learning. We show that a CNN model trained on an old task (or self-supervised proxy task) could be ``reprogrammed" to solve a new task by using our proposed lightweight (very cheap) reprogramming parameter. With the help of CLR, we have a better stability-plasticity trade-off to solve continual learning problems: To maintain stability and retain previous task ability, we use a common task-agnostic immutable part as the shared ``anchor" parameter set. We then add task-specific lightweight reprogramming parameters to reinterpret the outputs of the immutable parts, to enable plasticity and integrate new knowledge. To learn sequential tasks, we only train the lightweight reprogramming parameters to learn each new task. Reprogramming parameters are task-specific and exclusive to each task, which makes our method immune to catastrophic forgetting. To minimize the parameter requirement of reprogramming to learn new tasks, we make reprogramming lightweight by only adjusting essential kernels and learning channel-wise linear mappings from anchor parameters to task-specific domain knowledge. We show that, for general CNNs, the CLR parameter increase is less than 0.6\% for any new task. Our method outperforms 13 state-of-the-art continual learning baselines on a new challenging sequence of 53 image classification datasets. Code and data are available at https://github.com/gyhandy/Channel-wise-Lightweight-Reprogramming

Lightweight Learner for Shared Knowledge Lifelong Learning

In Lifelong Learning (LL), agents continually learn as they encounter new conditions and tasks. Most current LL is limited to a single agent that learns tasks sequentially. Dedicated LL machinery is then deployed to mitigate the forgetting of old tasks as new tasks are learned. This is inherently slow. We propose a new Shared Knowledge Lifelong Learning (SKILL) challenge, which deploys a decentralized population of LL agents that each sequentially learn different tasks, with all agents operating independently and in parallel. After learning their respective tasks, agents share and consolidate their knowledge over a decentralized communication network, so that, in the end, all agents can master all tasks. We present one solution to SKILL which uses Lightweight Lifelong Learning (LLL) agents, where the goal is to facilitate efficient sharing by minimizing the fraction of the agent that is specialized for any given task. Each LLL agent thus consists of a common task-agnostic immutable part, where most parameters are, and individual task-specific modules that contain fewer parameters but are adapted to each task. Agents share their task-specific modules, plus summary information ("task anchors") representing their tasks in the common task-agnostic latent space of all agents. Receiving agents register each received task-specific module using the corresponding anchor. Thus, every agent improves its ability to solve new tasks each time new task-specific modules and anchors are received. On a new, very challenging SKILL-102 dataset with 102 image classification tasks (5,033 classes in total, 2,041,225 training, 243,464 validation, and 243,464 test images), we achieve much higher (and SOTA) accuracy over 8 LL baselines, while also achieving near perfect parallelization. Code and data can be found at https://github.com/gyhandy/Shared-Knowledge-Lifelong-Learning

Detecting Mitoses with a Convolutional Neural Network for MIDOG 2022 Challenge

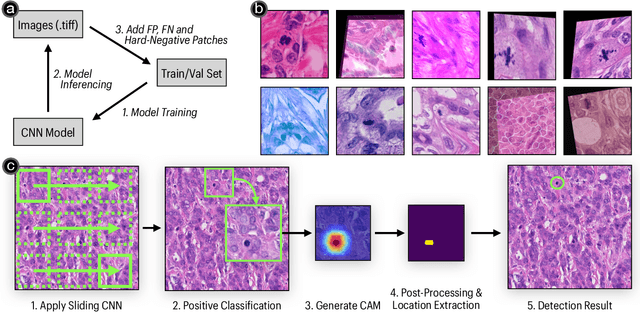
This work presents a mitosis detection method with only one vanilla Convolutional Neural Network (CNN). Our approach consists of two steps: given an image, we first apply a CNN using a sliding window technique to extract patches that have mitoses; we then calculate each extracted patch's class activation map to obtain the mitosis's precise location. To increase the model generalizability, we train the CNN with a series of data augmentation techniques, a loss that copes with noise-labeled images, and an active learning strategy. Our approach achieved an F1 score of 0.7323 with an EfficientNet-b3 model in the preliminary test phase of the MIDOG 2022 challenge.

High Dimensional Differentially Private Stochastic Optimization with Heavy-tailed Data

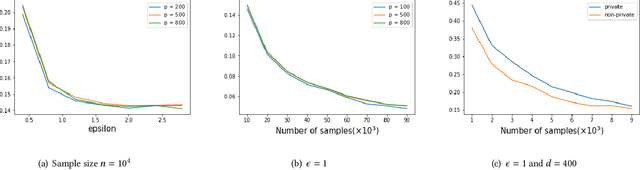
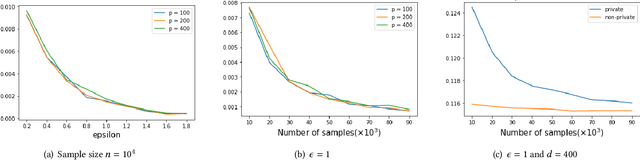
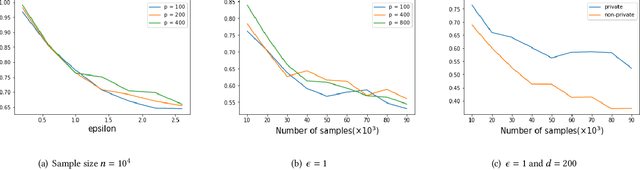
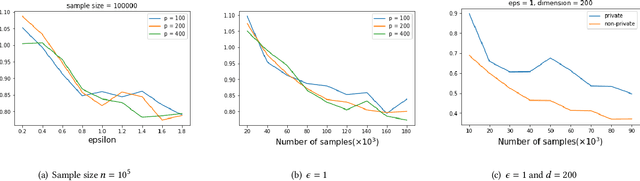
As one of the most fundamental problems in machine learning, statistics and differential privacy, Differentially Private Stochastic Convex Optimization (DP-SCO) has been extensively studied in recent years. However, most of the previous work can only handle either regular data distribution or irregular data in the low dimensional space case. To better understand the challenges arising from irregular data distribution, in this paper we provide the first study on the problem of DP-SCO with heavy-tailed data in the high dimensional space. In the first part we focus on the problem over some polytope constraint (such as the $\ell_1$-norm ball). We show that if the loss function is smooth and its gradient has bounded second order moment, it is possible to get a (high probability) error bound (excess population risk) of $\tilde{O}(\frac{\log d}{(n\epsilon)^\frac{1}{3}})$ in the $\epsilon$-DP model, where $n$ is the sample size and $d$ is the dimensionality of the underlying space. Next, for LASSO, if the data distribution that has bounded fourth-order moments, we improve the bound to $\tilde{O}(\frac{\log d}{(n\epsilon)^\frac{2}{5}})$ in the $(\epsilon, \delta)$-DP model. In the second part of the paper, we study sparse learning with heavy-tailed data. We first revisit the sparse linear model and propose a truncated DP-IHT method whose output could achieve an error of $\tilde{O}(\frac{s^{*2}\log d}{n\epsilon})$, where $s^*$ is the sparsity of the underlying parameter. Then we study a more general problem over the sparsity ({\em i.e.,} $\ell_0$-norm) constraint, and show that it is possible to achieve an error of $\tilde{O}(\frac{s^{*\frac{3}{2}}\log d}{n\epsilon})$, which is also near optimal up to a factor of $\tilde{O}{(\sqrt{s^*})}$, if the loss function is smooth and strongly convex.