Stability of Mean-Field Variational Inference

Mean-field variational inference (MFVI) is a widely used method for approximating high-dimensional probability distributions by product measures. This paper studies the stability properties of the mean-field approximation when the target distribution varies within the class of strongly log-concave measures. We establish dimension-free Lipschitz continuity of the MFVI optimizer with respect to the target distribution, measured in the 2-Wasserstein distance, with Lipschitz constant inversely proportional to the log-concavity parameter. Under additional regularity conditions, we further show that the MFVI optimizer depends differentiably on the target potential and characterize the derivative by a partial differential equation. Methodologically, we follow a novel approach to MFVI via linearized optimal transport: the non-convex MFVI problem is lifted to a convex optimization over transport maps with a fixed base measure, enabling the use of calculus of variations and functional analysis. We discuss several applications of our results to robust Bayesian inference and empirical Bayes, including a quantitative Bernstein--von Mises theorem for MFVI, as well as to distributed stochastic control.

Binary Spatial Random Field Reconstruction from Non-Gaussian Inhomogeneous Time-series Observations

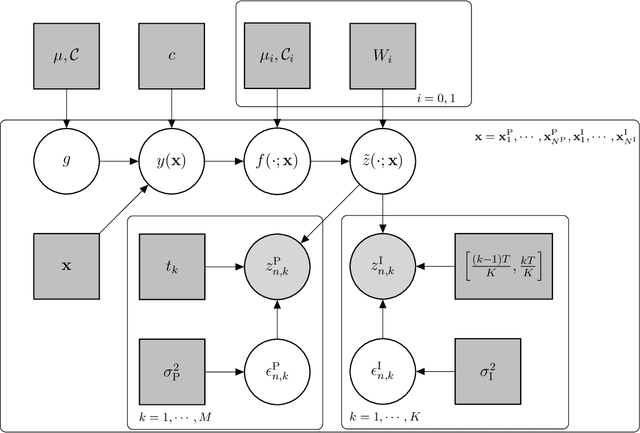
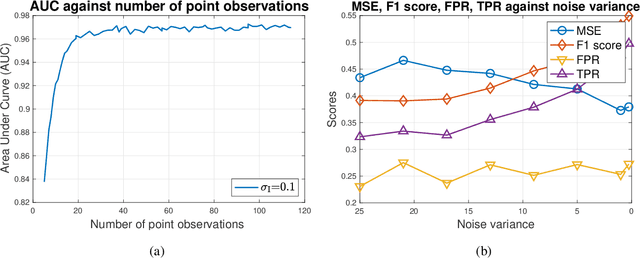
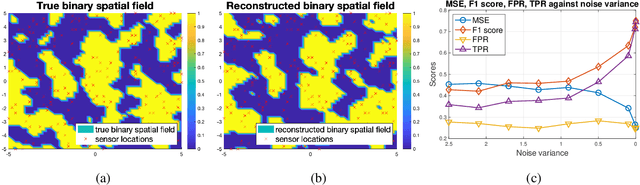
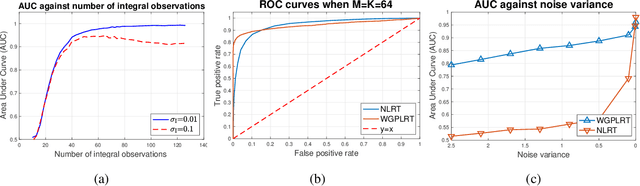
We develop a new model for binary spatial random field reconstruction of a physical phenomenon which is partially observed via inhomogeneous time-series data. We consider a sensor network deployed over a vast geographical region where sensors observe temporal processes and transmit compressed observations to the Fusion Center (FC). Two types of sensors are considered; one collects point observations at specific time points while the other collects integral observations over time intervals. Subsequently, the FC uses the compressed observations to infer the spatial phenomenon modeled as a binary spatial random field. We show that the resulting posterior predictive distribution is intractable and develop a tractable two-step procedure to perform inference. First, we develop procedures to approximately perform Likelihood Ratio Tests on the time-series data, for both point sensors and integral sensors, in order to compress the temporal observations to a single bit. Second, after the compressed observations are transmitted to the FC, we develop a Spatial Best Linear Unbiased Estimator (S-BLUE) in order for the FC to reconstruct the binary spatial random field at an arbitrary spatial location. Finally, we present a comprehensive study of the performance of the proposed approaches using both synthetic and real-world experiments. A weather dataset from the National Environment Agency (NEA) of Singapore with fields including temperature and relative humidity is used in the real-world experiments to validate the proposed approaches.

Balanced Meta-Softmax for Long-Tailed Visual Recognition

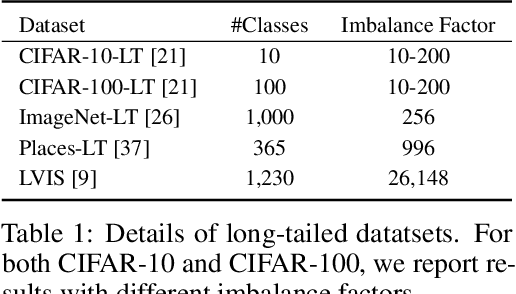
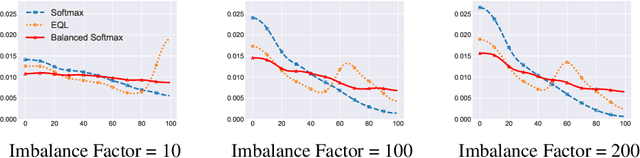
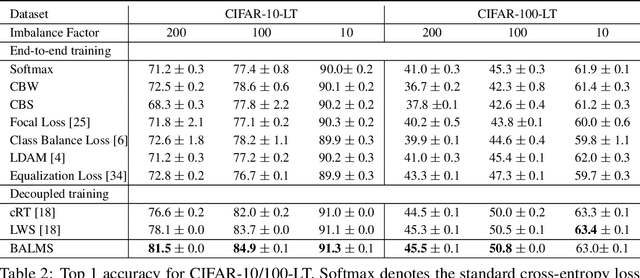
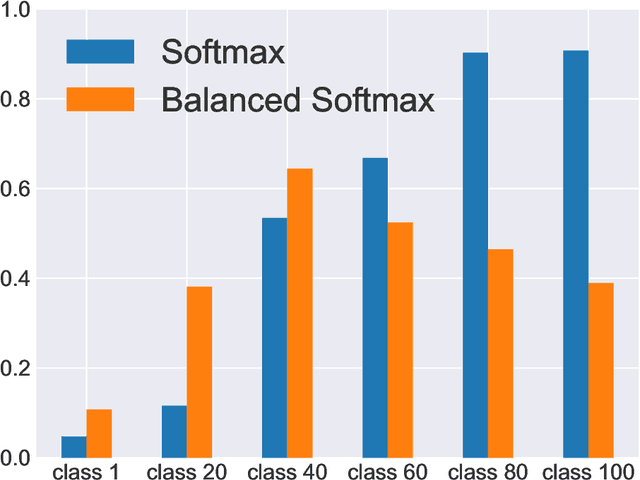
Deep classifiers have achieved great success in visual recognition. However, real-world data is long-tailed by nature, leading to the mismatch between training and testing distributions. In this paper, we show that Softmax function, though used in most classification tasks, gives a biased gradient estimation under the long-tailed setup. This paper presents Balanced Softmax, an elegant unbiased extension of Softmax, to accommodate the label distribution shift between training and testing. Theoretically, we derive the generalization bound for multiclass Softmax regression and show our loss minimizes the bound. In addition, we introduce Balanced Meta-Softmax, applying a complementary Meta Sampler to estimate the optimal class sample rate and further improve long-tailed learning. In our experiments, we demonstrate that Balanced Meta-Softmax outperforms state-of-the-art long-tailed classification solutions on both visual recognition and instance segmentation tasks.