Optimal Top-Two Method for Best Arm Identification and Fluid Analysis

Top-$2$ methods have become popular in solving the best arm identification (BAI) problem. The best arm, or the arm with the largest mean amongst finitely many, is identified through an algorithm that at any sequential step independently pulls the empirical best arm, with a fixed probability $\beta$, and pulls the best challenger arm otherwise. The probability of incorrect selection is guaranteed to lie below a specified $\delta >0$. Information theoretic lower bounds on sample complexity are well known for BAI problem and are matched asymptotically as $\delta \rightarrow 0$ by computationally demanding plug-in methods. The above top 2 algorithm for any $\beta \in (0,1)$ has sample complexity within a constant of the lower bound. However, determining the optimal $\beta$ that matches the lower bound has proven difficult. In this paper, we address this and propose an optimal top-2 type algorithm. We consider a function of allocations anchored at a threshold. If it exceeds the threshold then the algorithm samples the empirical best arm. Otherwise, it samples the challenger arm. We show that the proposed algorithm is optimal as $\delta \rightarrow 0$. Our analysis relies on identifying a limiting fluid dynamics of allocations that satisfy a series of ordinary differential equations pasted together and that describe the asymptotic path followed by our algorithm. We rely on the implicit function theorem to show existence and uniqueness of these fluid ode's and to show that the proposed algorithm remains close to the ode solution.

Comparing skill of historical rainfall data based monsoon rainfall prediction in India with NCEP-NWP forecasts

In this draft we consider the problem of forecasting rainfall across India during the four monsoon months, one day as well as three days in advance. We train neural networks using historical daily gridded precipitation data for India obtained from IMD for the time period $1901- 2022$, at a spatial resolution of $1^{\circ} \times 1^{\circ}$. This is compared with the numerical weather prediction (NWP) forecasts obtained from NCEP (National Centre for Environmental Prediction) available for the period 2011-2022. We conduct a detailed country wide analysis and separately analyze some of the most populated cities in India. Our conclusion is that forecasts obtained by applying deep learning to historical rainfall data are more accurate compared to NWP forecasts as well as predictions based on persistence. On average, compared to our predictions, forecasts from NCEP-NWP model have about 34% higher error for a single day prediction, and over 68% higher error for a three day prediction. Similarly, persistence estimates report a 29% higher error in a single day forecast, and over 54% error in a three day forecast. We further observe that data up to 20 days in the past is useful in reducing errors of one and three day forecasts, when a transformer based learning architecture, and to a lesser extent when an LSTM is used. A key conclusion suggested by our preliminary analysis is that NWP forecasts can be substantially improved upon through more and diverse data relevant to monsoon prediction combined with carefully selected neural network architecture.

Optimal Best-Arm Identification in Bandits with Access to Offline Data

Learning paradigms based purely on offline data as well as those based solely on sequential online learning have been well-studied in the literature. In this paper, we consider combining offline data with online learning, an area less studied but of obvious practical importance. We consider the stochastic $K$-armed bandit problem, where our goal is to identify the arm with the highest mean in the presence of relevant offline data, with confidence $1-\delta$. We conduct a lower bound analysis on policies that provide such $1-\delta$ probabilistic correctness guarantees. We develop algorithms that match the lower bound on sample complexity when $\delta$ is small. Our algorithms are computationally efficient with an average per-sample acquisition cost of $\tilde{O}(K)$, and rely on a careful characterization of the optimality conditions of the lower bound problem.

Regret Minimization in Heavy-Tailed Bandits

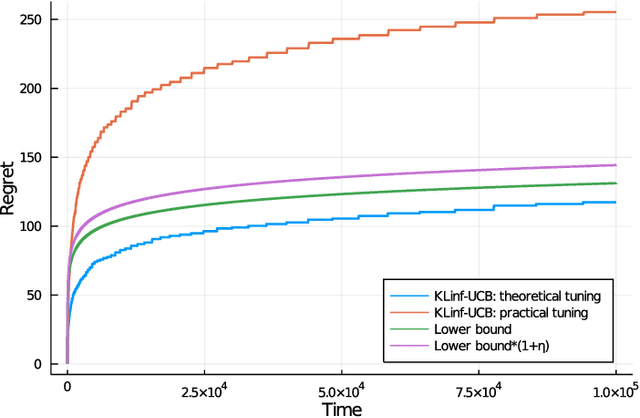
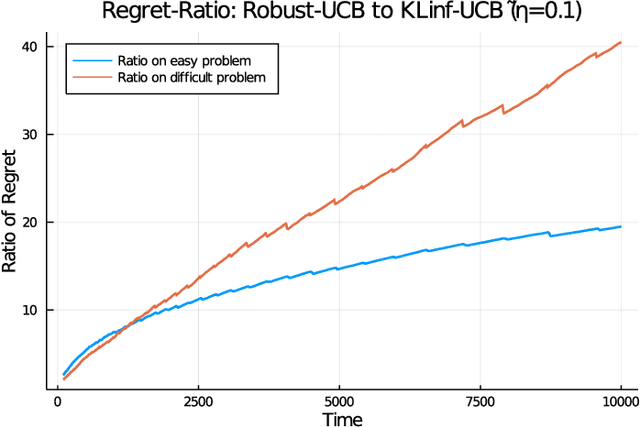
We revisit the classic regret-minimization problem in the stochastic multi-armed bandit setting when the arm-distributions are allowed to be heavy-tailed. Regret minimization has been well studied in simpler settings of either bounded support reward distributions or distributions that belong to a single parameter exponential family. We work under the much weaker assumption that the moments of order $(1+\epsilon)$ are uniformly bounded by a known constant B, for some given $\epsilon > 0$. We propose an optimal algorithm that matches the lower bound exactly in the first-order term. We also give a finite-time bound on its regret. We show that our index concentrates faster than the well known truncated or trimmed empirical mean estimators for the mean of heavy-tailed distributions. Computing our index can be computationally demanding. To address this, we develop a batch-based algorithm that is optimal up to a multiplicative constant depending on the batch size. We hence provide a controlled trade-off between statistical optimality and computational cost.

Optimal Best-Arm Identification Methods for Tail-Risk Measures

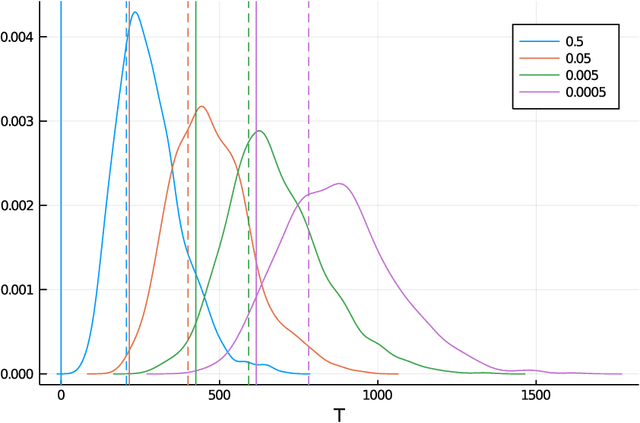
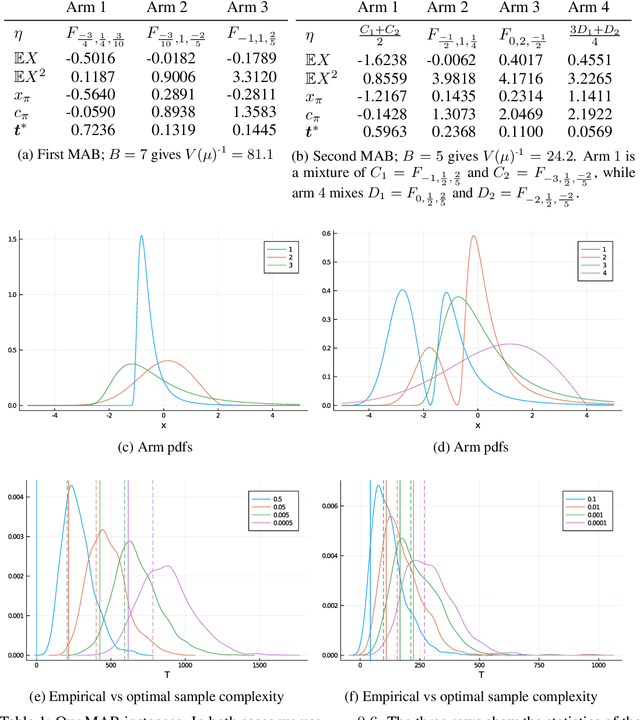
Conditional value-at-risk (CVaR) and value-at-risk (VaR) are popular tail-risk measures in finance and insurance industries where often the underlying probability distributions are heavy-tailed. We use the multi-armed bandit best-arm identification framework and consider the problem of identifying the arm-distribution from amongst finitely many that has the smallest CVaR or VaR. We first show that in the special case of arm-distributions belonging to a single-parameter exponential family, both these problems are equivalent to the best mean-arm identification problem, which is widely studied in the literature. This equivalence however is not true in general. We then propose optimal $\delta$-correct algorithms that act on general arm-distributions, including heavy-tailed distributions, that match the lower bound on the expected number of samples needed, asymptotically (as $ \delta$ approaches $0$). En-route, we also develop new non-asymptotic concentration inequalities for certain functions of these risk measures for the empirical distribution, that may have wider applicability.

Discriminative Learning via Adaptive Questioning

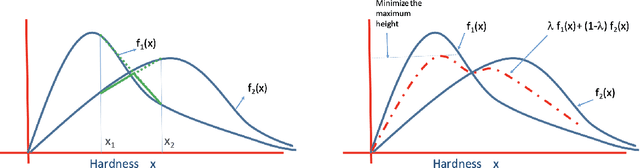
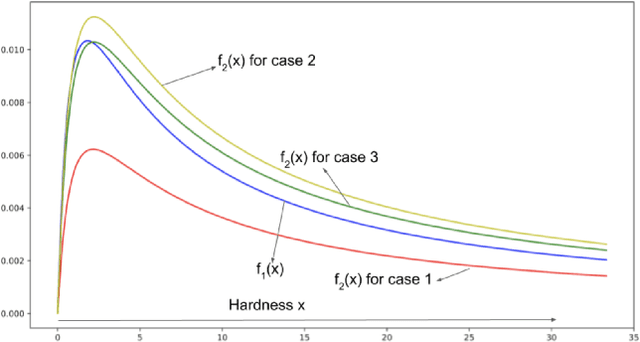
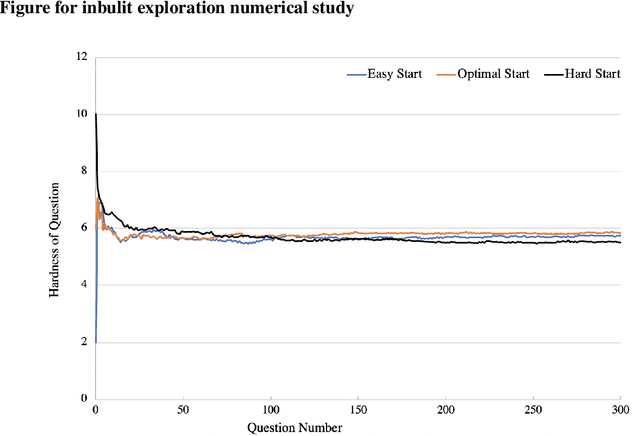
We consider the problem of designing an adaptive sequence of questions that optimally classify a candidate's ability into one of several categories or discriminative grades. A candidate's ability is modeled as an unknown parameter, which, together with the difficulty of the question asked, determines the likelihood with which s/he is able to answer a question correctly. The learning algorithm is only able to observe these noisy responses to its queries. We consider this problem from a fixed confidence-based $\delta$-correct framework, that in our setting seeks to arrive at the correct ability discrimination at the fastest possible rate while guaranteeing that the probability of error is less than a pre-specified and small $\delta$. In this setting we develop lower bounds on any sequential questioning strategy and develop geometrical insights into the problem structure both from primal and dual formulation. In addition, we arrive at algorithms that essentially match these lower bounds. Our key conclusions are that, asymptotically, any candidate needs to be asked questions at most at two (candidate ability-specific) levels, although, in a reasonably general framework, questions need to be asked only at a single level. Further, and interestingly, the problem structure facilitates endogenous exploration, so there is no need for a separately designed exploration stage in the algorithm.

Optimal best arm selection for general distributions

Given a finite set of unknown distributions $\textit{or arms}$ that can be sampled from, we consider the problem of identifying the one with the largest mean using a delta-correct algorithm (an adaptive, sequential algorithm that restricts the probability of error to a specified delta) that has minimum sample complexity. Lower bounds for delta-correct algorithms are well known. Further, delta-correct algorithms that match the lower bound asymptotically as delta reduces to zero have also been developed in literature when the arm distributions are restricted to a single parameter exponential family. In this paper, we first observe a negative result that some restrictions are essential as otherwise under a delta-correct algorithm, distributions with unbounded support would require an infinite number of samples in expectation. We then propose a delta-correct algorithm that matches the lower bound as delta reduces to zero under a mild restriction that a known bound on the expectation of a non-negative, increasing convex function (for example, the squared moment) of underlying random variables, exists. We also propose batch processing and identify optimal batch sizes to substantially speed up the proposed algorithm. This best arm selection problem is a well studied classic problem in the simulation community. It has many learning applications including in recommendation systems and in product selection.

Sample complexity of partition identification using multi-armed bandits

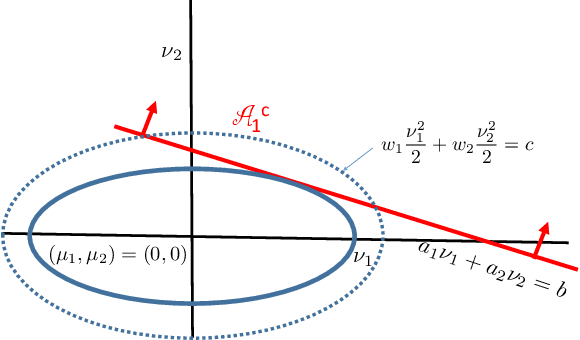
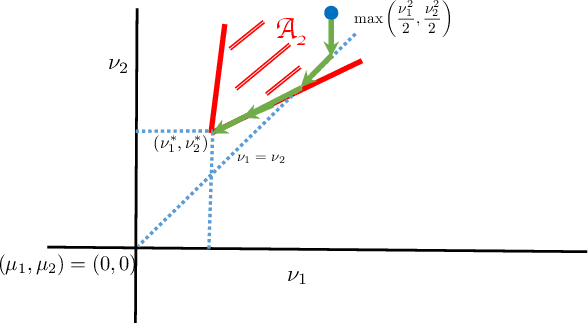
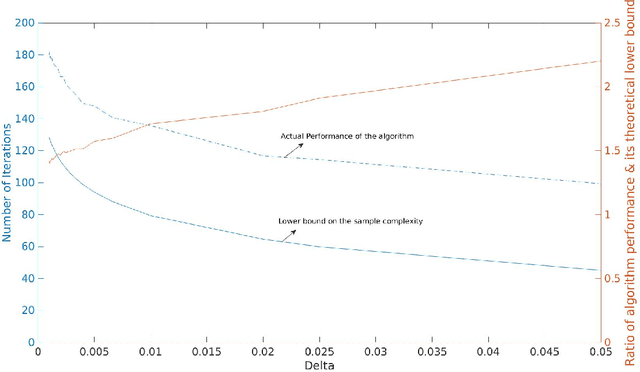
Given a vector of probability distributions, or arms, each of which can be sampled independently, we consider the problem of identifying the partition to which this vector belongs from a finitely partitioned universe of such vector of distributions. We study this as a pure exploration problem in multi armed bandit settings and develop sample complexity bounds on the total mean number of samples required for identifying the correct partition with high probability. This framework subsumes well studied problems in the literature such as finding the best arm or the best few arms. We consider distributions belonging to the single parameter exponential family and primarily consider partitions where the vector of means of arms lie either in a given set or its complement. The sets considered correspond to distributions where there exists a mean above a specified threshold, where the set is a half space and where either the set or its complement is convex. When the set is convex we restrict our analysis to its complement being a union of half spaces. In all these settings, we characterize the lower bounds on mean number of samples for each arm. Further, inspired by the lower bounds, and building upon Garivier and Kaufmann 2016, we propose algorithms that can match these bounds asymptotically with decreasing probability of error. Applications of this framework may be diverse. We briefly discuss a few associated with finance.

Selecting the best system and multi-armed bandits

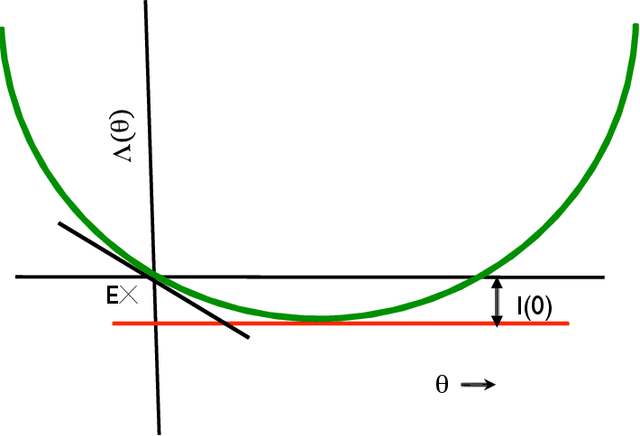
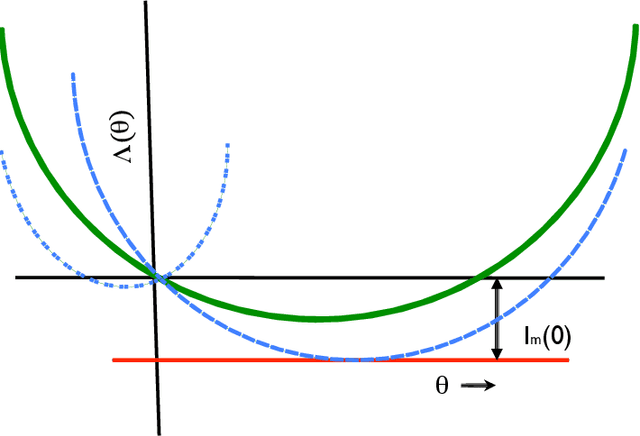
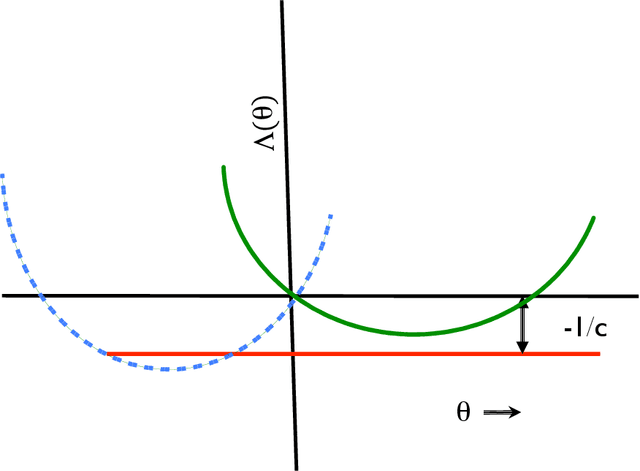
Consider the problem of finding a population or a probability distribution amongst many with the largest mean when these means are unknown but population samples can be simulated or otherwise generated. Typically, by selecting largest sample mean population, it can be shown that false selection probability decays at an exponential rate. Lately, researchers have sought algorithms that guarantee that this probability is restricted to a small $\delta$ in order $\log(1/\delta)$ computational time by estimating the associated large deviations rate function via simulation. We show that such guarantees are misleading when populations have unbounded support even when these may be light-tailed. Specifically, we show that any policy that identifies the correct population with probability at least $1-\delta$ for each problem instance requires infinite number of samples in expectation in making such a determination in any problem instance. This suggests that some restrictions are essential on populations to devise $O(\log(1/\delta))$ algorithms with $1 - \delta$ correctness guarantees. We note that under restriction on population moments, such methods are easily designed, and that sequential methods from stochastic multi-armed bandit literature can be adapted to devise such algorithms.