CRIMED: Lower and Upper Bounds on Regret for Bandits with Unbounded Stochastic Corruption

We investigate the regret-minimisation problem in a multi-armed bandit setting with arbitrary corruptions. Similar to the classical setup, the agent receives rewards generated independently from the distribution of the arm chosen at each time. However, these rewards are not directly observed. Instead, with a fixed $\varepsilon\in (0,\frac{1}{2})$, the agent observes a sample from the chosen arm's distribution with probability $1-\varepsilon$, or from an arbitrary corruption distribution with probability $\varepsilon$. Importantly, we impose no assumptions on these corruption distributions, which can be unbounded. In this setting, accommodating potentially unbounded corruptions, we establish a problem-dependent lower bound on regret for a given family of arm distributions. We introduce CRIMED, an asymptotically-optimal algorithm that achieves the exact lower bound on regret for bandits with Gaussian distributions with known variance. Additionally, we provide a finite-sample analysis of CRIMED's regret performance. Notably, CRIMED can effectively handle corruptions with $\varepsilon$ values as high as $\frac{1}{2}$. Furthermore, we develop a tight concentration result for medians in the presence of arbitrary corruptions, even with $\varepsilon$ values up to $\frac{1}{2}$, which may be of independent interest. We also discuss an extension of the algorithm for handling misspecification in Gaussian model.

AdaStop: sequential testing for efficient and reliable comparisons of Deep RL Agents

The reproducibility of many experimental results in Deep Reinforcement Learning (RL) is under question. To solve this reproducibility crisis, we propose a theoretically sound methodology to compare multiple Deep RL algorithms. The performance of one execution of a Deep RL algorithm is random so that independent executions are needed to assess it precisely. When comparing several RL algorithms, a major question is how many executions must be made and how can we assure that the results of such a comparison is theoretically sound. Researchers in Deep RL often use less than 5 independent executions to compare algorithms: we claim that this is not enough in general. Moreover, when comparing several algorithms at once, the error of each comparison accumulates and must be taken into account with a multiple tests procedure to preserve low error guarantees. To address this problem in a statistically sound way, we introduce AdaStop, a new statistical test based on multiple group sequential tests. When comparing algorithms, AdaStop adapts the number of executions to stop as early as possible while ensuring that we have enough information to distinguish algorithms that perform better than the others in a statistical significant way. We prove both theoretically and empirically that AdaStop has a low probability of making an error (Family-Wise Error). Finally, we illustrate the effectiveness of AdaStop in multiple use-cases, including toy examples and difficult cases such as Mujoco environments.

Bandits Corrupted by Nature: Lower Bounds on Regret and Robust Optimistic Algorithm

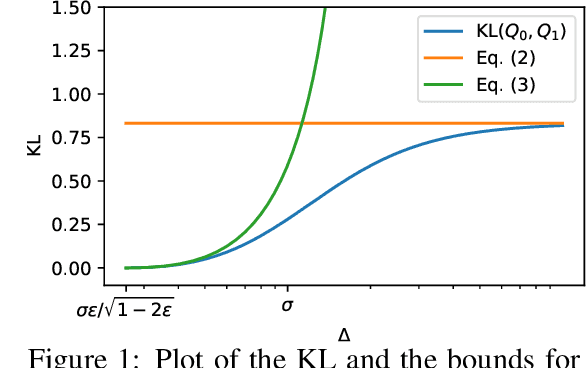
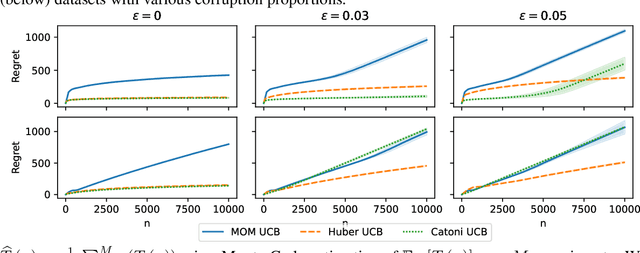
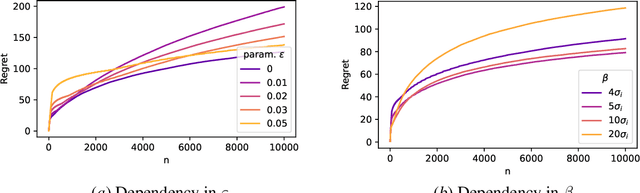
In this paper, we study the stochastic bandits problem with $k$ unknown heavy-tailed and corrupted reward distributions or arms with time-invariant corruption distributions. At each iteration, the player chooses an arm. Given the arm, the environment returns an uncorrupted reward with probability $1-\varepsilon$ and an arbitrarily corrupted reward with probability $\varepsilon$. In our setting, the uncorrupted reward might be heavy-tailed and the corrupted reward might be unbounded. We prove a lower bound on the regret indicating that the corrupted and heavy-tailed bandits are strictly harder than uncorrupted or light-tailed bandits. We observe that the environments can be categorised into hardness regimes depending on the suboptimality gap $\Delta$, variance $\sigma$, and corruption proportion $\epsilon$. Following this, we design a UCB-type algorithm, namely HuberUCB, that leverages Huber's estimator for robust mean estimation. HuberUCB leads to tight upper bounds on regret in the proposed corrupted and heavy-tailed setting. To derive the upper bound, we prove a novel concentration inequality for Huber's estimator, which might be of independent interest.

Excess risk bounds in robust empirical risk minimization

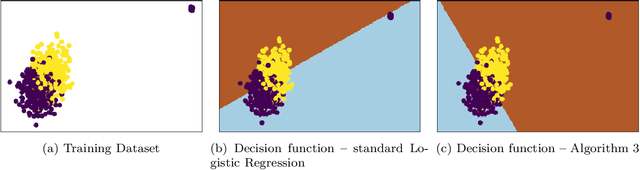
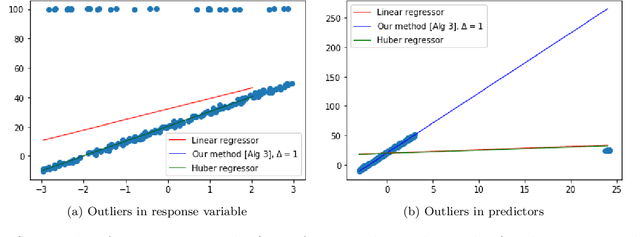
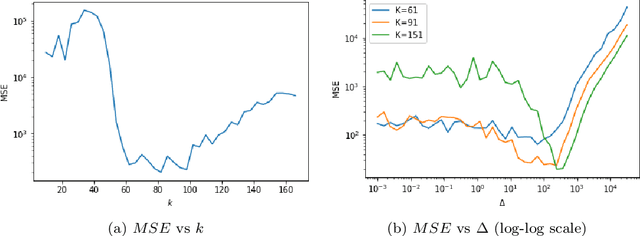
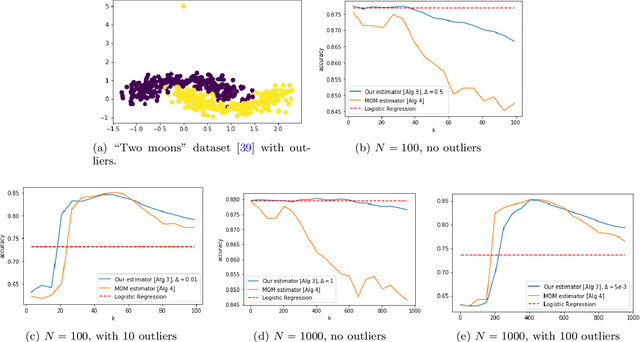
This paper investigates robust versions of the general empirical risk minimization algorithm, one of the core techniques underlying modern statistical methods. Success of the empirical risk minimization is based on the fact that for a "well-behaved" stochastic process $\left\{ f(X), \ f\in \mathcal F\right\}$ indexed by a class of functions $f\in \mathcal F$, averages $\frac{1}{N}\sum_{j=1}^N f(X_j)$ evaluated over a sample $X_1,\ldots,X_N$ of i.i.d. copies of $X$ provide good approximation to the expectations $\mathbb E f(X)$ uniformly over large classes $f\in \mathcal F$. However, this might no longer be true if the marginal distributions of the process are heavy-tailed or if the sample contains outliers. We propose a version of empirical risk minimization based on the idea of replacing sample averages by robust proxies of the expectation, and obtain high-confidence bounds for the excess risk of resulting estimators. In particular, we show that the excess risk of robust estimators can converge to $0$ at fast rates with respect to the sample size. We discuss implications of the main results to the linear and logistic regression problems, and evaluate the numerical performance of proposed methods on simulated and real data.