Kriging and Gaussian Process Interpolation for Georeferenced Data Augmentation

Data augmentation is a crucial step in the development of robust supervised learning models, especially when dealing with limited datasets. This study explores interpolation techniques for the augmentation of geo-referenced data, with the aim of predicting the presence of Commelina benghalensis L. in sugarcane plots in La R{\'e}union. Given the spatial nature of the data and the high cost of data collection, we evaluated two interpolation approaches: Gaussian processes (GPs) with different kernels and kriging with various variograms. The objectives of this work are threefold: (i) to identify which interpolation methods offer the best predictive performance for various regression algorithms, (ii) to analyze the evolution of performance as a function of the number of observations added, and (iii) to assess the spatial consistency of augmented datasets. The results show that GP-based methods, in particular with combined kernels (GP-COMB), significantly improve the performance of regression algorithms while requiring less additional data. Although kriging shows slightly lower performance, it is distinguished by a more homogeneous spatial coverage, a potential advantage in certain contexts.

Provably Efficient Exploration in Reward Machines with Low Regret

We study reinforcement learning (RL) for decision processes with non-Markovian reward, in which high-level knowledge of the task in the form of reward machines is available to the learner. We consider probabilistic reward machines with initially unknown dynamics, and investigate RL under the average-reward criterion, where the learning performance is assessed through the notion of regret. Our main algorithmic contribution is a model-based RL algorithm for decision processes involving probabilistic reward machines that is capable of exploiting the structure induced by such machines. We further derive high-probability and non-asymptotic bounds on its regret and demonstrate the gain in terms of regret over existing algorithms that could be applied, but obliviously to the structure. We also present a regret lower bound for the studied setting. To the best of our knowledge, the proposed algorithm constitutes the first attempt to tailor and analyze regret specifically for RL with probabilistic reward machines.

Hierarchical Subspaces of Policies for Continual Offline Reinforcement Learning

In dynamic domains such as autonomous robotics and video game simulations, agents must continuously adapt to new tasks while retaining previously acquired skills. This ongoing process, known as Continual Reinforcement Learning, presents significant challenges, including the risk of forgetting past knowledge and the need for scalable solutions as the number of tasks increases. To address these issues, we introduce HIerarchical LOW-rank Subspaces of Policies (HILOW), a novel framework designed for continual learning in offline navigation settings. HILOW leverages hierarchical policy subspaces to enable flexible and efficient adaptation to new tasks while preserving existing knowledge. We demonstrate, through a careful experimental study, the effectiveness of our method in both classical MuJoCo maze environments and complex video game-like simulations, showcasing competitive performance and satisfying adaptability according to classical continual learning metrics, in particular regarding memory usage. Our work provides a promising framework for real-world applications where continuous learning from pre-collected data is essential.

How to Shrink Confidence Sets for Many Equivalent Discrete Distributions?

We consider the situation when a learner faces a set of unknown discrete distributions $(p_k)_{k\in \mathcal K}$ defined over a common alphabet $\mathcal X$, and can build for each distribution $p_k$ an individual high-probability confidence set thanks to $n_k$ observations sampled from $p_k$. The set $(p_k)_{k\in \mathcal K}$ is structured: each distribution $p_k$ is obtained from the same common, but unknown, distribution q via applying an unknown permutation to $\mathcal X$. We call this \emph{permutation-equivalence}. The goal is to build refined confidence sets \emph{exploiting} this structural property. Like other popular notions of structure (Lipschitz smoothness, Linearity, etc.) permutation-equivalence naturally appears in machine learning problems, and to benefit from its potential gain calls for a specific approach. We present a strategy to effectively exploit permutation-equivalence, and provide a finite-time high-probability bound on the size of the refined confidence sets output by the strategy. Since a refinement is not possible for too few observations in general, under mild technical assumptions, our finite-time analysis establish when the number of observations $(n_k)_{k\in \mathcal K}$ are large enough so that the output confidence sets improve over initial individual sets. We carefully characterize this event and the corresponding improvement. Further, our result implies that the size of confidence sets shrink at asymptotic rates of $O(1/\sqrt{\sum_{k\in \mathcal K} n_k})$ and $O(1/\max_{k\in K} n_{k})$, respectively for elements inside and outside the support of q, when the size of each individual confidence set shrinks at respective rates of $O(1/\sqrt{n_k})$ and $O(1/n_k)$. We illustrate the practical benefit of exploiting permutation equivalence on a reinforcement learning task.

Power Mean Estimation in Stochastic Monte-Carlo Tree_Search

Monte-Carlo Tree Search (MCTS) is a widely-used strategy for online planning that combines Monte-Carlo sampling with forward tree search. Its success relies on the Upper Confidence bound for Trees (UCT) algorithm, an extension of the UCB method for multi-arm bandits. However, the theoretical foundation of UCT is incomplete due to an error in the logarithmic bonus term for action selection, leading to the development of Fixed-Depth-MCTS with a polynomial exploration bonus to balance exploration and exploitation~\citep{shah2022journal}. Both UCT and Fixed-Depth-MCTS suffer from biased value estimation: the weighted sum underestimates the optimal value, while the maximum valuation overestimates it~\citep{coulom2006efficient}. The power mean estimator offers a balanced solution, lying between the average and maximum values. Power-UCT~\citep{dam2019generalized} incorporates this estimator for more accurate value estimates but its theoretical analysis remains incomplete. This paper introduces Stochastic-Power-UCT, an MCTS algorithm using the power mean estimator and tailored for stochastic MDPs. We analyze its polynomial convergence in estimating root node values and show that it shares the same convergence rate of $\mathcal{O}(n^{-1/2})$, with $n$ is the number of visited trajectories, as Fixed-Depth-MCTS, with the latter being a special case of the former. Our theoretical results are validated with empirical tests across various stochastic MDP environments.

CRIMED: Lower and Upper Bounds on Regret for Bandits with Unbounded Stochastic Corruption

We investigate the regret-minimisation problem in a multi-armed bandit setting with arbitrary corruptions. Similar to the classical setup, the agent receives rewards generated independently from the distribution of the arm chosen at each time. However, these rewards are not directly observed. Instead, with a fixed $\varepsilon\in (0,\frac{1}{2})$, the agent observes a sample from the chosen arm's distribution with probability $1-\varepsilon$, or from an arbitrary corruption distribution with probability $\varepsilon$. Importantly, we impose no assumptions on these corruption distributions, which can be unbounded. In this setting, accommodating potentially unbounded corruptions, we establish a problem-dependent lower bound on regret for a given family of arm distributions. We introduce CRIMED, an asymptotically-optimal algorithm that achieves the exact lower bound on regret for bandits with Gaussian distributions with known variance. Additionally, we provide a finite-sample analysis of CRIMED's regret performance. Notably, CRIMED can effectively handle corruptions with $\varepsilon$ values as high as $\frac{1}{2}$. Furthermore, we develop a tight concentration result for medians in the presence of arbitrary corruptions, even with $\varepsilon$ values up to $\frac{1}{2}$, which may be of independent interest. We also discuss an extension of the algorithm for handling misspecification in Gaussian model.

Monte-Carlo tree search with uncertainty propagation via optimal transport

This paper introduces a novel backup strategy for Monte-Carlo Tree Search (MCTS) designed for highly stochastic and partially observable Markov decision processes. We adopt a probabilistic approach, modeling both value and action-value nodes as Gaussian distributions. We introduce a novel backup operator that computes value nodes as the Wasserstein barycenter of their action-value children nodes; thus, propagating the uncertainty of the estimate across the tree to the root node. We study our novel backup operator when using a novel combination of $L^1$-Wasserstein barycenter with $\alpha$-divergence, by drawing a notable connection to the generalized mean backup operator. We complement our probabilistic backup operator with two sampling strategies, based on optimistic selection and Thompson sampling, obtaining our Wasserstein MCTS algorithm. We provide theoretical guarantees of asymptotic convergence to the optimal policy, and an empirical evaluation on several stochastic and partially observable environments, where our approach outperforms well-known related baselines.

AdaStop: sequential testing for efficient and reliable comparisons of Deep RL Agents

The reproducibility of many experimental results in Deep Reinforcement Learning (RL) is under question. To solve this reproducibility crisis, we propose a theoretically sound methodology to compare multiple Deep RL algorithms. The performance of one execution of a Deep RL algorithm is random so that independent executions are needed to assess it precisely. When comparing several RL algorithms, a major question is how many executions must be made and how can we assure that the results of such a comparison is theoretically sound. Researchers in Deep RL often use less than 5 independent executions to compare algorithms: we claim that this is not enough in general. Moreover, when comparing several algorithms at once, the error of each comparison accumulates and must be taken into account with a multiple tests procedure to preserve low error guarantees. To address this problem in a statistically sound way, we introduce AdaStop, a new statistical test based on multiple group sequential tests. When comparing algorithms, AdaStop adapts the number of executions to stop as early as possible while ensuring that we have enough information to distinguish algorithms that perform better than the others in a statistical significant way. We prove both theoretically and empirically that AdaStop has a low probability of making an error (Family-Wise Error). Finally, we illustrate the effectiveness of AdaStop in multiple use-cases, including toy examples and difficult cases such as Mujoco environments.

Bilinear Exponential Family of MDPs: Frequentist Regret Bound with Tractable Exploration and Planning

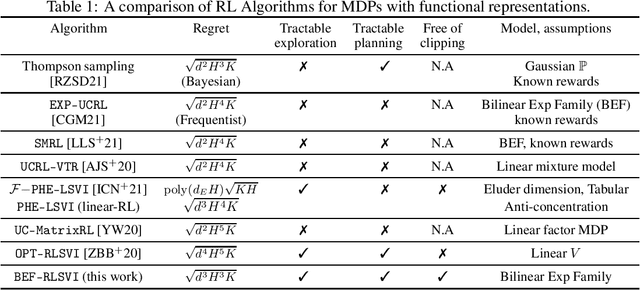
We study the problem of episodic reinforcement learning in continuous state-action spaces with unknown rewards and transitions. Specifically, we consider the setting where the rewards and transitions are modeled using parametric bilinear exponential families. We propose an algorithm, BEF-RLSVI, that a) uses penalized maximum likelihood estimators to learn the unknown parameters, b) injects a calibrated Gaussian noise in the parameter of rewards to ensure exploration, and c) leverages linearity of the exponential family with respect to an underlying RKHS to perform tractable planning. We further provide a frequentist regret analysis of BEF-RLSVI that yields an upper bound of $\tilde{\mathcal{O}}(\sqrt{d^3H^3K})$, where $d$ is the dimension of the parameters, $H$ is the episode length, and $K$ is the number of episodes. Our analysis improves the existing bounds for the bilinear exponential family of MDPs by $\sqrt{H}$ and removes the handcrafted clipping deployed in existing \RLSVI-type algorithms. Our regret bound is order-optimal with respect to $H$ and $K$.

Risk-aware linear bandits with convex loss

In decision-making problems such as the multi-armed bandit, an agent learns sequentially by optimizing a certain feedback. While the mean reward criterion has been extensively studied, other measures that reflect an aversion to adverse outcomes, such as mean-variance or conditional value-at-risk (CVaR), can be of interest for critical applications (healthcare, agriculture). Algorithms have been proposed for such risk-aware measures under bandit feedback without contextual information. In this work, we study contextual bandits where such risk measures can be elicited as linear functions of the contexts through the minimization of a convex loss. A typical example that fits within this framework is the expectile measure, which is obtained as the solution of an asymmetric least-square problem. Using the method of mixtures for supermartingales, we derive confidence sequences for the estimation of such risk measures. We then propose an optimistic UCB algorithm to learn optimal risk-aware actions, with regret guarantees similar to those of generalized linear bandits. This approach requires solving a convex problem at each round of the algorithm, which we can relax by allowing only approximated solution obtained by online gradient descent, at the cost of slightly higher regret. We conclude by evaluating the resulting algorithms on numerical experiments.