Partial Feedback Online Learning

We study partial-feedback online learning, where each instance admits a set of correct labels, but the learner only observes one correct label per round; any prediction within the correct set is counted as correct. This model captures settings such as language generation, where multiple responses may be valid but data provide only a single reference. We give a near-complete characterization of minimax regret for both deterministic and randomized learners in the set-realizable regime, i.e., in the regime where sublinear regret is generally attainable. For deterministic learners, we introduce the Partial-Feedback Littlestone dimension (PFLdim) and show it precisely governs learnability and minimax regret; technically, PFLdim cannot be defined via the standard version space, requiring a new collection version space viewpoint and an auxiliary dimension used only in the proof. We further develop the Partial-Feedback Measure Shattering dimension (PMSdim) to obtain tight bounds for randomized learners. We identify broad conditions ensuring inseparability between deterministic and randomized learnability (e.g., finite Helly number or nested-inclusion label structure), and extend the argument to set-valued online learning, resolving an open question of Raman et al. [2024b]. Finally, we show a sharp separation from weaker realistic and agnostic variants: outside set realizability, the problem can become information-theoretically intractable, with linear regret possible even for $|H|=2$. This highlights the need for fundamentally new, noise-sensitive complexity measures to meaningfully characterize learnability beyond set realizability.

High-Rank Irreducible Cartesian Tensor Decomposition and Bases of Equivariant Spaces

Irreducible Cartesian tensors (ICTs) play a crucial role in the design of equivariant graph neural networks, as well as in theoretical chemistry and chemical physics. Meanwhile, the design space of available linear operations on tensors that preserve symmetry presents a significant challenge. The ICT decomposition and a basis of this equivariant space are difficult to obtain for high-order tensors. After decades of research, we recently achieve an explicit ICT decomposition for $n=5$ \citep{bonvicini2024irreducible} with factorial time/space complexity. This work, for the first time, obtains decomposition matrices for ICTs up to rank $n=9$ with reduced and affordable complexity, by constructing what we call path matrices. The path matrices are obtained via performing chain-like contraction with Clebsch-Gordan matrices following the parentage scheme. We prove and leverage that the concatenation of path matrices is an orthonormal change-of-basis matrix between the Cartesian tensor product space and the spherical direct sum spaces. Furthermore, we identify a complete orthogonal basis for the equivariant space, rather than a spanning set \citep{pearce2023brauer}, through this path matrices technique. We further extend our result to the arbitrary tensor product and direct sum spaces, enabling free design between different spaces while keeping symmetry. The Python code is available in https://github.com/ShihaoShao-GH/ICT-decomposition-and-equivariant-bases where the $n=6,\dots,9$ ICT decomposition matrices are obtained in 1s, 3s, 11s, and 4m32s, respectively.

Free the Design Space of Equivariant Graph Neural Networks: High-Rank Irreducible Cartesian Tensor Decomposition and Bases of Equivariant Spaces

Irreducible Cartesian tensors (ICTs) play a crucial role in the design of equivariant graph neural networks, as well as in theoretical chemistry and chemical physics. Meanwhile, the design space of available linear operations on tensors that preserve symmetry presents a significant challenge. The ICT decomposition and a basis of this equivariant space are difficult to obtain for high-order tensors. After decades of research, we recently achieve an explicit ICT decomposition for $n=5$ \citep{bonvicini2024irreducible} with factorial time/space complexity. This work, for the first time, obtains decomposition matrices for ICTs up to rank $n=9$ with reduced and affordable complexity, by constructing what we call path matrices. The path matrices are obtained via performing chain-like contraction with Clebsch-Gordan matrices following the parentage scheme. We prove and leverage that the concatenation of path matrices is an orthonormal change-of-basis matrix between the Cartesian tensor product space and the spherical direct sum spaces. Furthermore, we identify a complete orthogonal basis for the equivariant space, rather than a spanning set \citep{pearce2023brauer}, through this path matrices technique. We further extend our result to the arbitrary tensor product and direct sum spaces, enabling free design between different spaces while keeping symmetry. The Python code is available in the appendix where the $n=6,\dots,9$ ICT decomposition matrices are obtained in <0.1s, 0.5s, 1s, 3s, 11s, and 4m32s, respectively.

FreeCG: Free the Design Space of Clebsch-Gordan Transform for machine learning force field

The Clebsch-Gordan Transform (CG transform) effectively encodes many-body interactions. Many studies have proven its accuracy in depicting atomic environments, although this comes with high computational needs. The computational burden of this challenge is hard to reduce due to the need for permutation equivariance, which limits the design space of the CG transform layer. We show that, implementing the CG transform layer on permutation-invariant inputs allows complete freedom in the design of this layer without affecting symmetry. Developing further on this premise, our idea is to create a CG transform layer that operates on permutation-invariant abstract edges generated from real edge information. We bring in group CG transform with sparse path, abstract edges shuffling, and attention enhancer to form a powerful and efficient CG transform layer. Our method, known as FreeCG, achieves State-of-The-Art (SoTA) results in force prediction for MD17, rMD17, MD22, and property prediction in QM9 datasets with notable enhancement. It introduces a novel paradigm for carrying out efficient and expressive CG transform in future geometric neural network designs.

Global Features are All You Need for Image Retrieval and Reranking

Image retrieval systems conventionally use a two-stage paradigm, leveraging global features for initial retrieval and local features for reranking. However, the scalability of this method is often limited due to the significant storage and computation cost incurred by local feature matching in the reranking stage. In this paper, we present SuperGlobal, a novel approach that exclusively employs global features for both stages, improving efficiency without sacrificing accuracy. SuperGlobal introduces key enhancements to the retrieval system, specifically focusing on the global feature extraction and reranking processes. For extraction, we identify sub-optimal performance when the widely-used ArcFace loss and Generalized Mean (GeM) pooling methods are combined and propose several new modules to improve GeM pooling. In the reranking stage, we introduce a novel method to update the global features of the query and top-ranked images by only considering feature refinement with a small set of images, thus being very compute and memory efficient. Our experiments demonstrate substantial improvements compared to the state of the art in standard benchmarks. Notably, on the Revisited Oxford+1M Hard dataset, our single-stage results improve by 7.1%, while our two-stage gain reaches 3.7% with a strong 64,865x speedup. Our two-stage system surpasses the current single-stage state-of-the-art by 16.3%, offering a scalable, accurate alternative for high-performing image retrieval systems with minimal time overhead. Code: https://github.com/ShihaoShao-GH/SuperGlobal.

1st Place Solution in Google Universal Images Embedding

This paper presents the 1st place solution for the Google Universal Images Embedding Competition on Kaggle. The highlighted part of our solution is based on 1) A novel way to conduct training and fine-tuning; 2) The idea of a better ensemble in the pool of models that make embedding; 3) The potential trade-off between fine-tuning on high-resolution and overlapping patches; 4) The potential factors to work for the dynamic margin. Our solution reaches 0.728 in the private leader board, which achieve 1st place in Google Universal Images Embedding Competition.

A layer-stress learning framework universally augments deep neural network tasks

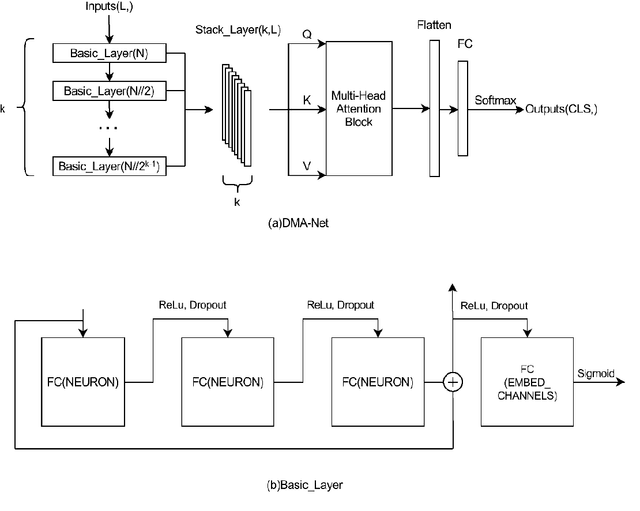
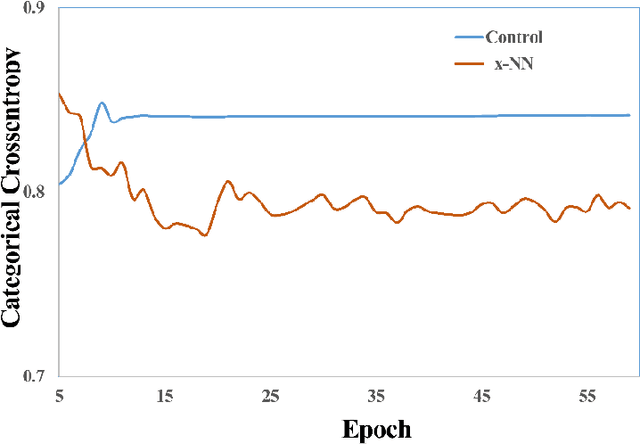
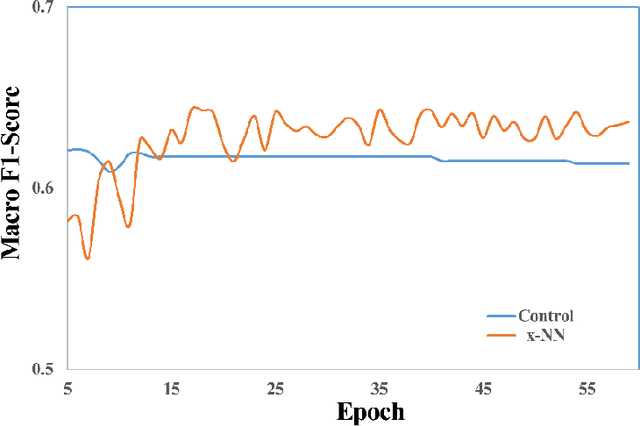
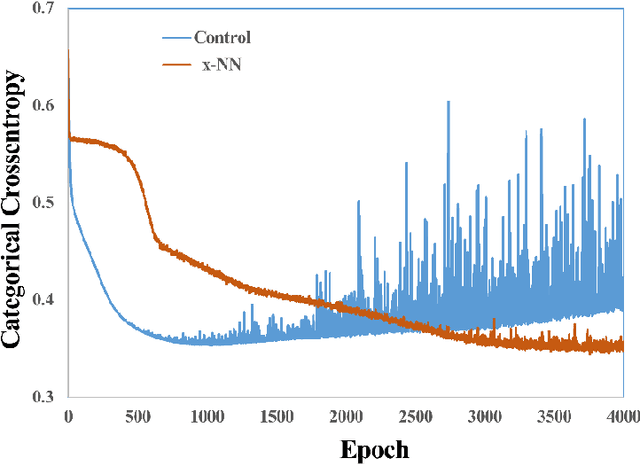
Deep neural networks (DNN) such as Multi-Layer Perception (MLP) and Convolutional Neural Networks (CNN) represent one of the most established deep learning algorithms. Given the tremendous effects of the number of hidden layers on network architecture and performance, it is very important to choose the number of hidden layers but still a serious challenge. More importantly, the current network architectures can only process the information from the last layer of the feature extractor, which greatly limited us to further improve its performance. Here we presented a layer-stress deep learning framework (x-NN) which implemented automatic and wise depth decision on shallow or deep feature map in a deep network through firstly designing enough number of layers and then trading off them by Multi-Head Attention Block. The x-NN can make use of features from various depth layers through attention allocation and then help to make final decision as well. As a result, x-NN showed outstanding prediction ability in the Alzheimer's Disease Classification Technique Challenge PRCV 2021, in which it won the top laurel and outperformed all other AI models. Moreover, the performance of x-NN was verified by one more AD neuroimaging dataset and other AI tasks.