A Closer Look at Hardware-Friendly Weight Quantization

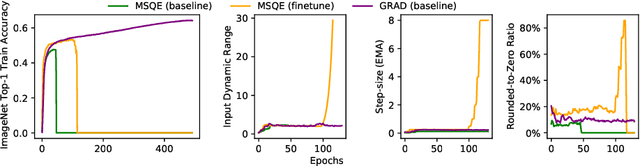
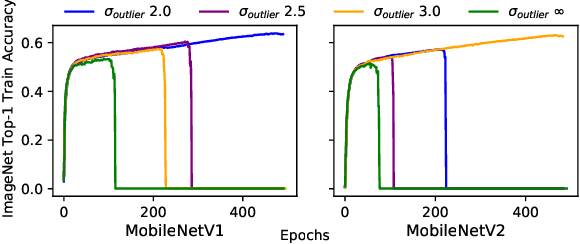
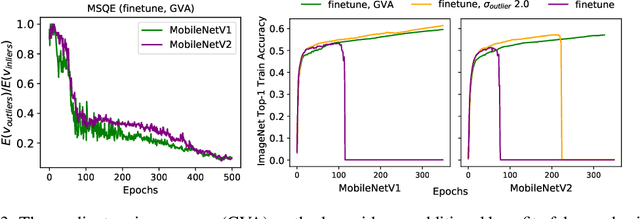
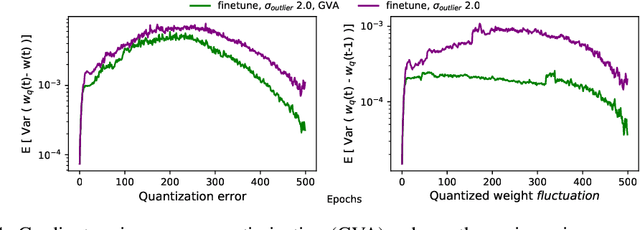
Quantizing a Deep Neural Network (DNN) model to be used on a custom accelerator with efficient fixed-point hardware implementations, requires satisfying many stringent hardware-friendly quantization constraints to train the model. We evaluate the two main classes of hardware-friendly quantization methods in the context of weight quantization: the traditional Mean Squared Quantization Error (MSQE)-based methods and the more recent gradient-based methods. We study the two methods on MobileNetV1 and MobileNetV2 using multiple empirical metrics to identify the sources of performance differences between the two classes, namely, sensitivity to outliers and convergence instability of the quantizer scaling factor. Using those insights, we propose various techniques to improve the performance of both quantization methods - they fix the optimization instability issues present in the MSQE-based methods during quantization of MobileNet models and allow us to improve validation performance of the gradient-based methods by 4.0% and 3.3% for MobileNetV1 and MobileNetV2 on ImageNet respectively.

On the Generalization Mystery in Deep Learning

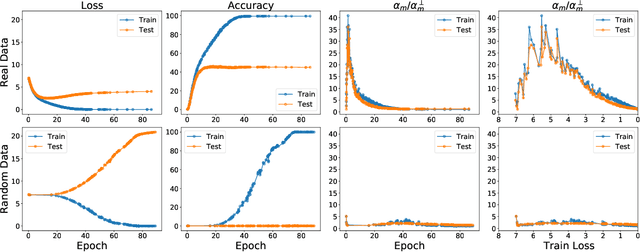
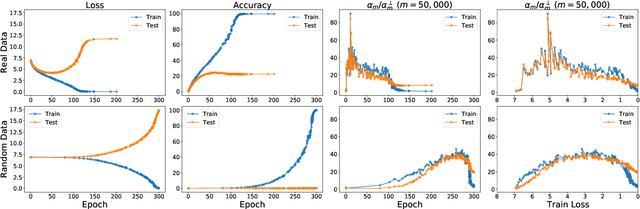
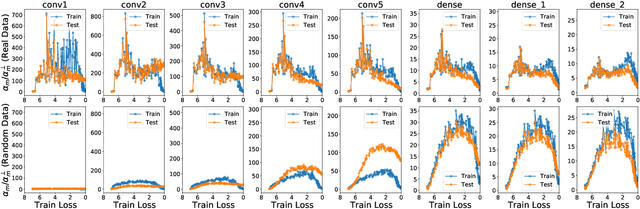
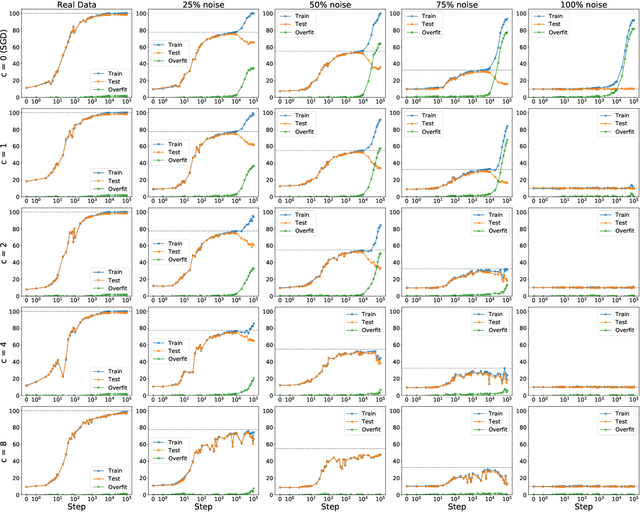
The generalization mystery in deep learning is the following: Why do over-parameterized neural networks trained with gradient descent (GD) generalize well on real datasets even though they are capable of fitting random datasets of comparable size? Furthermore, from among all solutions that fit the training data, how does GD find one that generalizes well (when such a well-generalizing solution exists)? We argue that the answer to both questions lies in the interaction of the gradients of different examples during training. Intuitively, if the per-example gradients are well-aligned, that is, if they are coherent, then one may expect GD to be (algorithmically) stable, and hence generalize well. We formalize this argument with an easy to compute and interpretable metric for coherence, and show that the metric takes on very different values on real and random datasets for several common vision networks. The theory also explains a number of other phenomena in deep learning, such as why some examples are reliably learned earlier than others, why early stopping works, and why it is possible to learn from noisy labels. Moreover, since the theory provides a causal explanation of how GD finds a well-generalizing solution when one exists, it motivates a class of simple modifications to GD that attenuate memorization and improve generalization. Generalization in deep learning is an extremely broad phenomenon, and therefore, it requires an equally general explanation. We conclude with a survey of alternative lines of attack on this problem, and argue that the proposed approach is the most viable one on this basis.

TIGRIS: An Informed Sampling-based Algorithm for Informative Path Planning

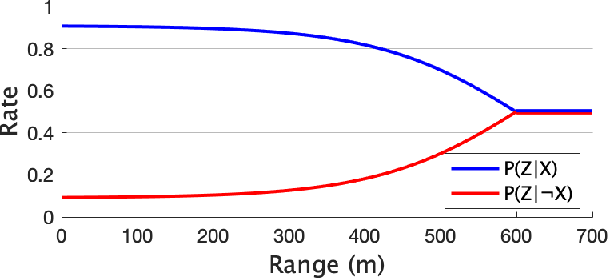
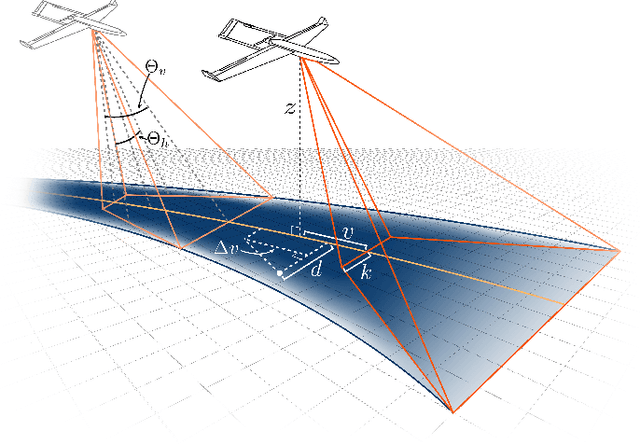
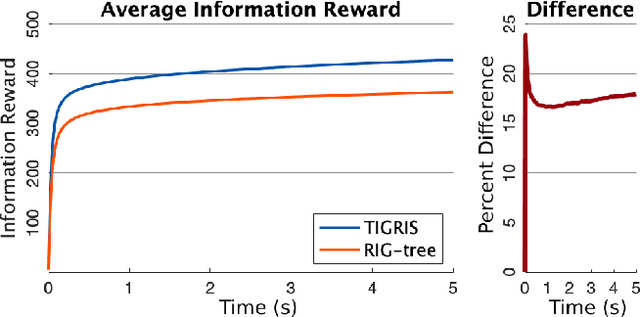
Informative path planning is an important and challenging problem in robotics that remains to be solved in a manner that allows for wide-spread implementation and real-world practical adoption. Among various reasons for this, one is the lack of approaches that allow for informative path planning in high-dimensional spaces and non-trivial sensor constraints. In this work we present a sampling-based approach that allows us to tackle the challenges of large and high-dimensional search spaces. This is done by performing informed sampling in the high-dimensional continuous space and incorporating potential information gain along edges in the reward estimation. This method rapidly generates a global path that maximizes information gain for the given path budget constraints. We discuss the details of our implementation for an example use case of searching for multiple objects of interest in a large search space using a fixed-wing UAV with a forward-facing camera. We compare our approach to a sampling-based planner baseline and demonstrate how our contributions allow our approach to consistently out-perform the baseline by $18.0\%$. With this we thus present a practical and generalizable informative path planning framework that can be used for very large environments, limited budgets, and high dimensional search spaces, such as robots with motion constraints or high-dimensional configuration spaces.

Enabling Binary Neural Network Training on the Edge

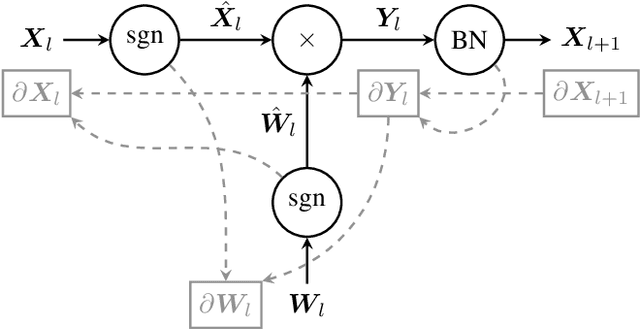
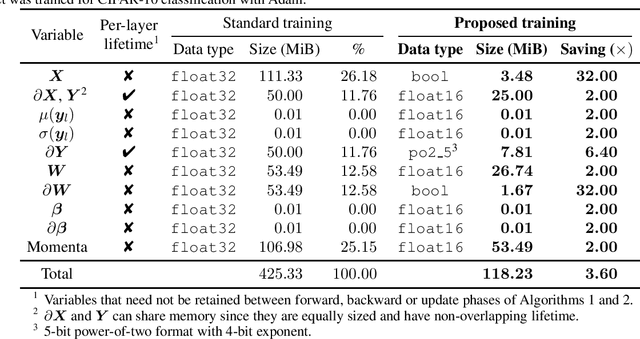
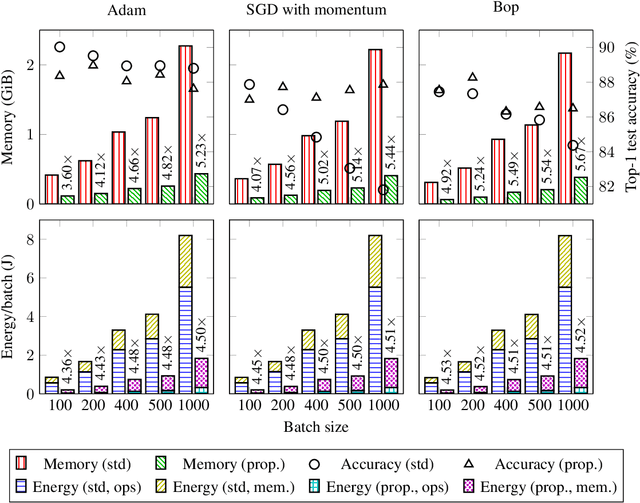
The ever-growing computational demands of increasingly complex machine learning models frequently necessitate the use of powerful cloud-based infrastructure for their training. Binary neural networks are known to be promising candidates for on-device inference due to their extreme compute and memory savings over higher-precision alternatives. In this paper, we demonstrate that they are also strongly robust to gradient quantization, thereby making the training of modern models on the edge a practical reality. We introduce a low-cost binary neural network training strategy exhibiting sizable memory footprint reductions and energy savings vs Courbariaux & Bengio's standard approach. Against the latter, we see coincident memory requirement and energy consumption drops of 2--6$\times$, while reaching similar test accuracy in comparable time, across a range of small-scale models trained to classify popular datasets. We also showcase ImageNet training of ResNetE-18, achieving a 3.12$\times$ memory reduction over the aforementioned standard. Such savings will allow for unnecessary cloud offloading to be avoided, reducing latency, increasing energy efficiency and safeguarding privacy.

Apollo: Transferable Architecture Exploration

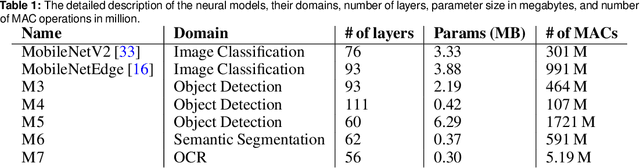
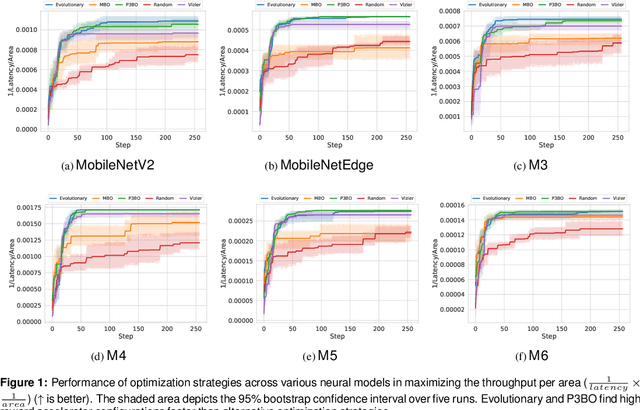
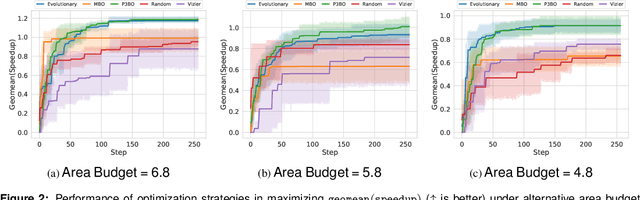
The looming end of Moore's Law and ascending use of deep learning drives the design of custom accelerators that are optimized for specific neural architectures. Architecture exploration for such accelerators forms a challenging constrained optimization problem over a complex, high-dimensional, and structured input space with a costly to evaluate objective function. Existing approaches for accelerator design are sample-inefficient and do not transfer knowledge between related optimizations tasks with different design constraints, such as area and/or latency budget, or neural architecture configurations. In this work, we propose a transferable architecture exploration framework, dubbed Apollo, that leverages recent advances in black-box function optimization for sample-efficient accelerator design. We use this framework to optimize accelerator configurations of a diverse set of neural architectures with alternative design constraints. We show that our framework finds high reward design configurations (up to 24.6% speedup) more sample-efficiently than a baseline black-box optimization approach. We further show that by transferring knowledge between target architectures with different design constraints, Apollo is able to find optimal configurations faster and often with better objective value (up to 25% improvements). This encouraging outcome portrays a promising path forward to facilitate generating higher quality accelerators.

Logic Synthesis Meets Machine Learning: Trading Exactness for Generalization

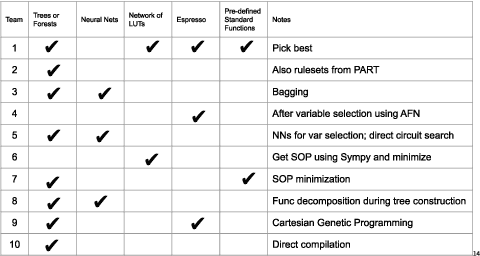
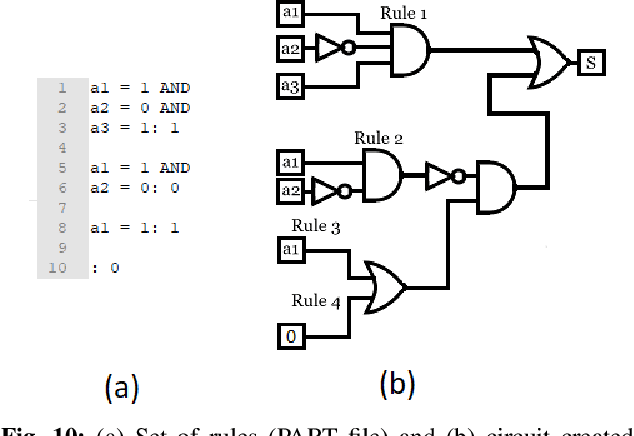
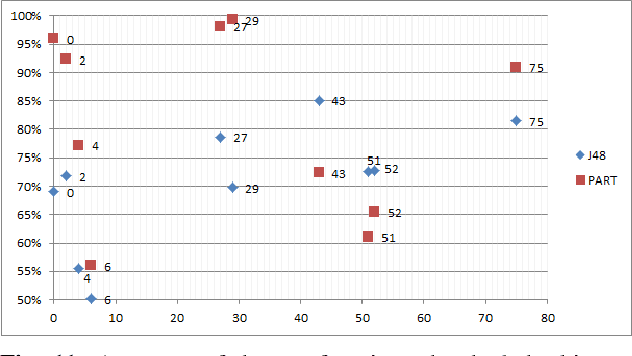
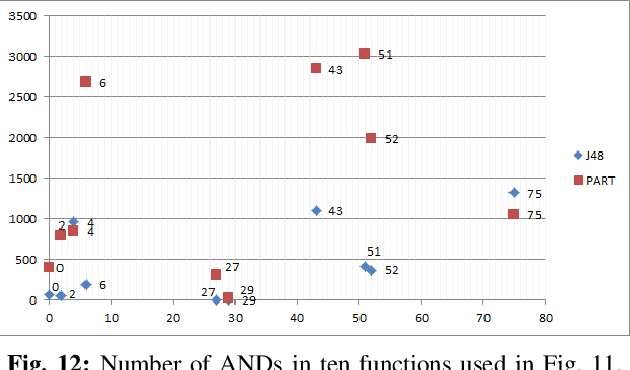
Logic synthesis is a fundamental step in hardware design whose goal is to find structural representations of Boolean functions while minimizing delay and area. If the function is completely-specified, the implementation accurately represents the function. If the function is incompletely-specified, the implementation has to be true only on the care set. While most of the algorithms in logic synthesis rely on SAT and Boolean methods to exactly implement the care set, we investigate learning in logic synthesis, attempting to trade exactness for generalization. This work is directly related to machine learning where the care set is the training set and the implementation is expected to generalize on a validation set. We present learning incompletely-specified functions based on the results of a competition conducted at IWLS 2020. The goal of the competition was to implement 100 functions given by a set of care minterms for training, while testing the implementation using a set of validation minterms sampled from the same function. We make this benchmark suite available and offer a detailed comparative analysis of the different approaches to learning

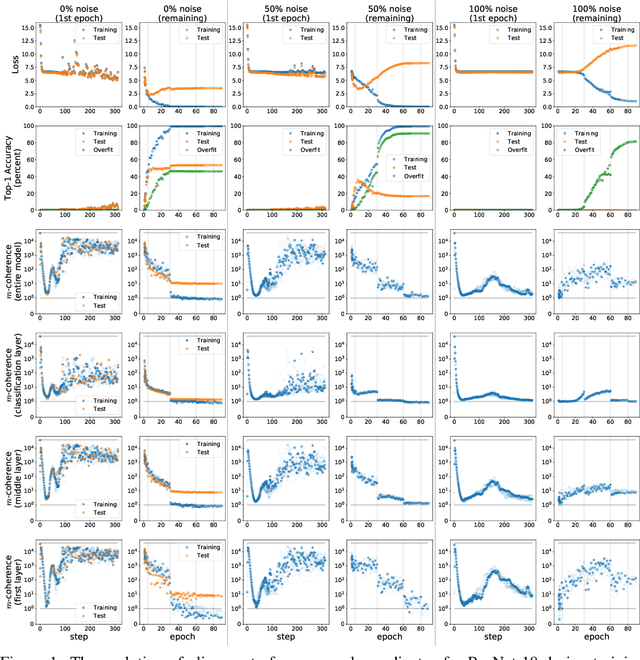
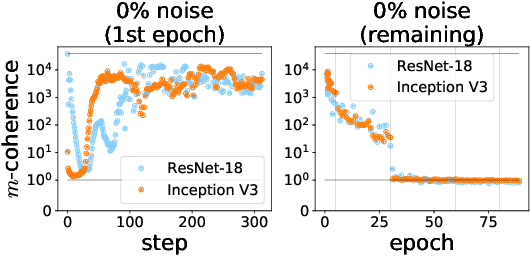
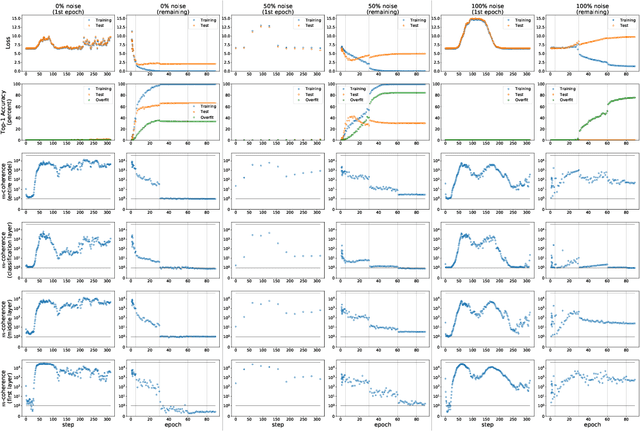
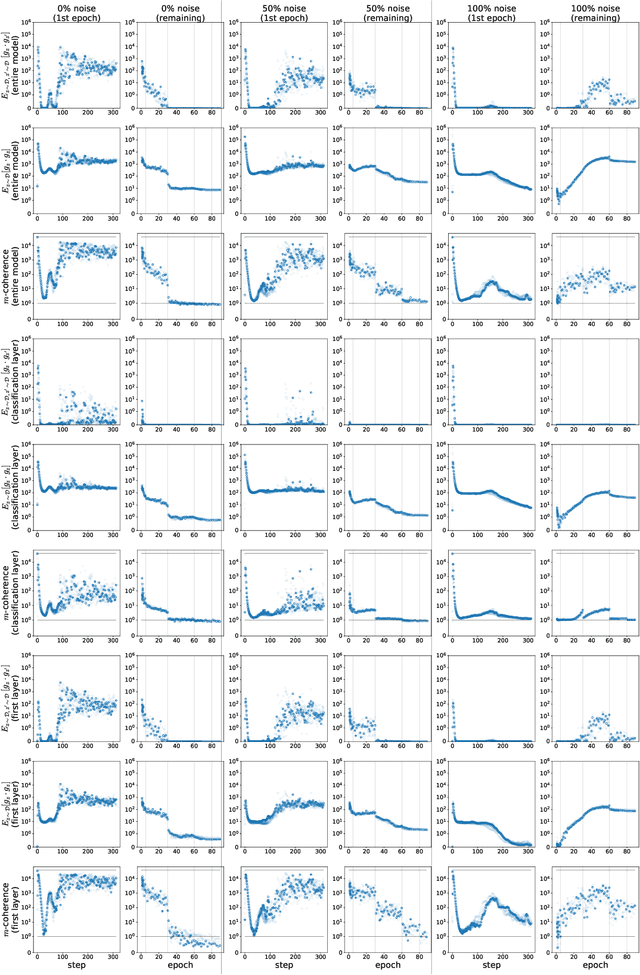
Making Coherence Out of Nothing At All: Measuring the Evolution of Gradient Alignment

We propose a new metric ($m$-coherence) to experimentally study the alignment of per-example gradients during training. Intuitively, given a sample of size $m$, $m$-coherence is the number of examples in the sample that benefit from a small step along the gradient of any one example on average. We show that compared to other commonly used metrics, $m$-coherence is more interpretable, cheaper to compute ($O(m)$ instead of $O(m^2)$) and mathematically cleaner. (We note that $m$-coherence is closely connected to gradient diversity, a quantity previously used in some theoretical bounds.) Using $m$-coherence, we study the evolution of alignment of per-example gradients in ResNet and Inception models on ImageNet and several variants with label noise, particularly from the perspective of the recently proposed Coherent Gradients (CG) theory that provides a simple, unified explanation for memorization and generalization [Chatterjee, ICLR 20]. Although we have several interesting takeaways, our most surprising result concerns memorization. Naively, one might expect that when training with completely random labels, each example is fitted independently, and so $m$-coherence should be close to 1. However, this is not the case: $m$-coherence reaches much higher values during training (100s), indicating that over-parameterized neural networks find common patterns even in scenarios where generalization is not possible. A detailed analysis of this phenomenon provides both a deeper confirmation of CG, but at the same point puts into sharp relief what is missing from the theory in order to provide a complete explanation of generalization in neural networks.

Explaining Memorization and Generalization: A Large-Scale Study with Coherent Gradients

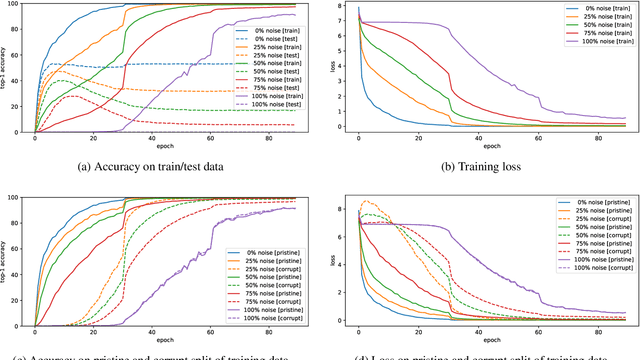
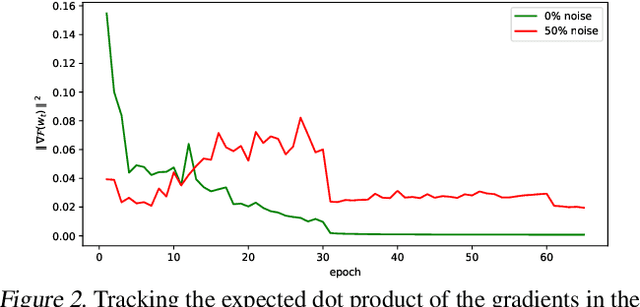
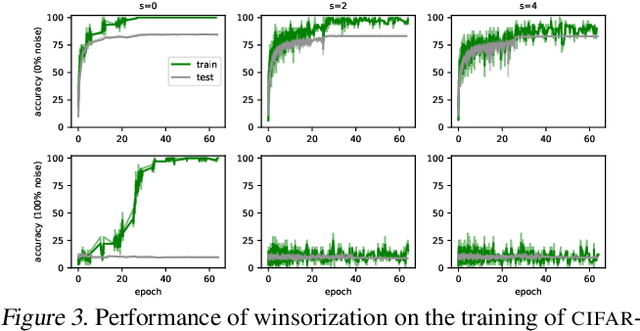
Coherent Gradients is a recently proposed hypothesis to explain why over-parameterized neural networks trained with gradient descent generalize well even though they have sufficient capacity to memorize the training set. Inspired by random forests, Coherent Gradients proposes that (Stochastic) Gradient Descent (SGD) finds common patterns amongst examples (if such common patterns exist) since descent directions that are common to many examples add up in the overall gradient, and thus the biggest changes to the network parameters are those that simultaneously help many examples. The original Coherent Gradients paper validated the theory through causal intervention experiments on shallow, fully connected networks on MNIST. In this work, we perform similar intervention experiments on more complex architectures (such as VGG, Inception and ResNet) on more complex datasets (such as CIFAR-10 and ImageNet). Our results are in good agreement with the small scale study in the original paper, thus providing the first validation of coherent gradients in more practically relevant settings. We also confirm in these settings that suppressing incoherent updates by natural modifications to SGD can significantly reduce overfitting--lending credence to the hypothesis that memorization occurs when few examples are responsible for most of the gradient used in the update. Furthermore, we use the coherent gradients theory to explore a new characterization of why some examples are learned earlier than other examples, i.e., "easy" and "hard" examples.

Coherent Gradients: An Approach to Understanding Generalization in Gradient Descent-based Optimization

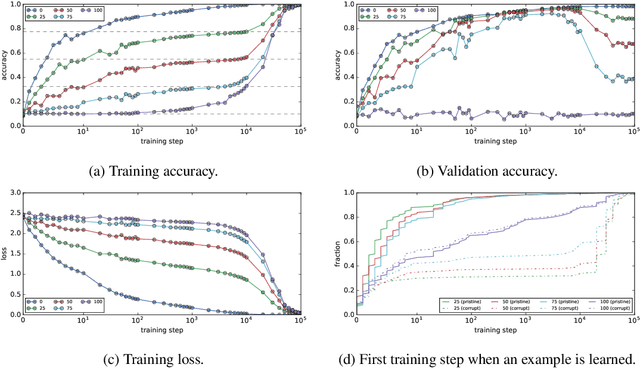
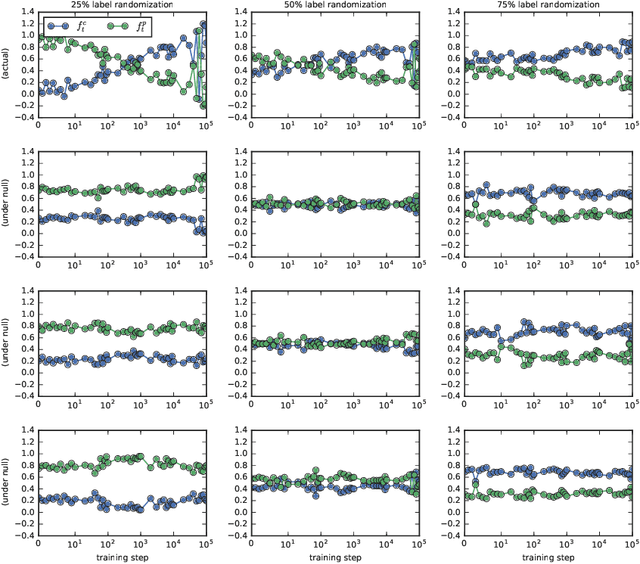
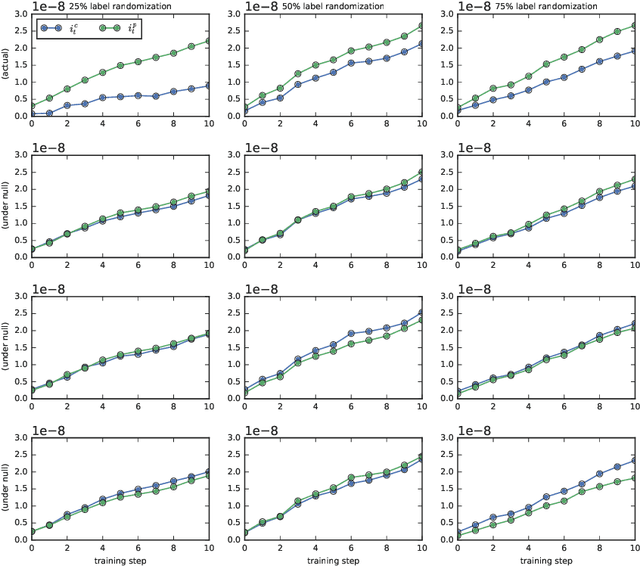
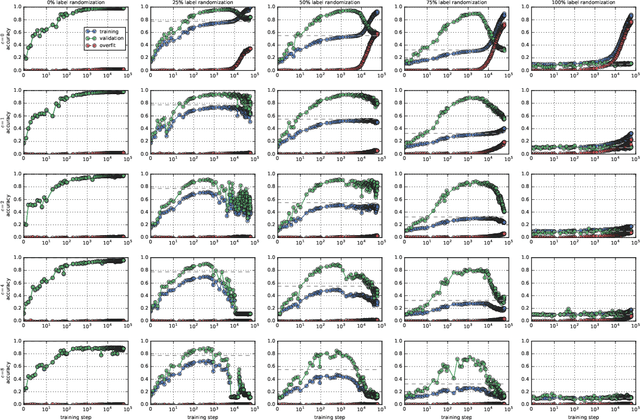
An open question in the Deep Learning community is why neural networks trained with Gradient Descent generalize well on real datasets even though they are capable of fitting random data. We propose an approach to answering this question based on a hypothesis about the dynamics of gradient descent that we call Coherent Gradients: Gradients from similar examples are similar and so the overall gradient is stronger in certain directions where these reinforce each other. Thus changes to the network parameters during training are biased towards those that (locally) simultaneously benefit many examples when such similarity exists. We support this hypothesis with heuristic arguments and perturbative experiments and outline how this can explain several common empirical observations about Deep Learning. Furthermore, our analysis is not just descriptive, but prescriptive. It suggests a natural modification to gradient descent that can greatly reduce overfitting.