Most General Explanations of Tree Ensembles

Explainable Artificial Intelligence (XAI) is critical for attaining trust in the operation of AI systems. A key question of an AI system is ``why was this decision made this way''. Formal approaches to XAI use a formal model of the AI system to identify abductive explanations. While abductive explanations may be applicable to a large number of inputs sharing the same concrete values, more general explanations may be preferred for numeric inputs. So-called inflated abductive explanations give intervals for each feature ensuring that any input whose values fall withing these intervals is still guaranteed to make the same prediction. Inflated explanations cover a larger portion of the input space, and hence are deemed more general explanations. But there can be many (inflated) abductive explanations for an instance. Which is the best? In this paper, we show how to find a most general abductive explanation for an AI decision. This explanation covers as much of the input space as possible, while still being a correct formal explanation of the model's behaviour. Given that we only want to give a human one explanation for a decision, the most general explanation gives us the explanation with the broadest applicability, and hence the one most likely to seem sensible. (The paper has been accepted at IJCAI2025 conference.)

Formal Explanations for Neuro-Symbolic AI

Despite the practical success of Artificial Intelligence (AI), current neural AI algorithms face two significant issues. First, the decisions made by neural architectures are often prone to bias and brittleness. Second, when a chain of reasoning is required, neural systems often perform poorly. Neuro-symbolic artificial intelligence is a promising approach that tackles these (and other) weaknesses by combining the power of neural perception and symbolic reasoning. Meanwhile, the success of AI has made it critical to understand its behaviour, leading to the development of explainable artificial intelligence (XAI). While neuro-symbolic AI systems have important advantages over purely neural AI, we still need to explain their actions, which are obscured by the interactions of the neural and symbolic components. To address the issue, this paper proposes a formal approach to explaining the decisions of neuro-symbolic systems. The approach hinges on the use of formal abductive explanations and on solving the neuro-symbolic explainability problem hierarchically. Namely, it first computes a formal explanation for the symbolic component of the system, which serves to identify a subset of the individual parts of neural information that needs to be explained. This is followed by explaining only those individual neural inputs, independently of each other, which facilitates succinctness of hierarchical formal explanations and helps to increase the overall performance of the approach. Experimental results for a few complex reasoning tasks demonstrate practical efficiency of the proposed approach, in comparison to purely neural systems, from the perspective of explanation size, explanation time, training time, model sizes, and the quality of explanations reported.

NEUSIS: A Compositional Neuro-Symbolic Framework for Autonomous Perception, Reasoning, and Planning in Complex UAV Search Missions

This paper addresses the problem of autonomous UAV search missions, where a UAV must locate specific Entities of Interest (EOIs) within a time limit, based on brief descriptions in large, hazard-prone environments with keep-out zones. The UAV must perceive, reason, and make decisions with limited and uncertain information. We propose NEUSIS, a compositional neuro-symbolic system designed for interpretable UAV search and navigation in realistic scenarios. NEUSIS integrates neuro-symbolic visual perception, reasoning, and grounding (GRiD) to process raw sensory inputs, maintains a probabilistic world model for environment representation, and uses a hierarchical planning component (SNaC) for efficient path planning. Experimental results from simulated urban search missions using AirSim and Unreal Engine show that NEUSIS outperforms a state-of-the-art (SOTA) vision-language model and a SOTA search planning model in success rate, search efficiency, and 3D localization. These results demonstrate the effectiveness of our compositional neuro-symbolic approach in handling complex, real-world scenarios, making it a promising solution for autonomous UAV systems in search missions.

Distance-Restricted Explanations: Theoretical Underpinnings & Efficient Implementation

The uses of machine learning (ML) have snowballed in recent years. In many cases, ML models are highly complex, and their operation is beyond the understanding of human decision-makers. Nevertheless, some uses of ML models involve high-stakes and safety-critical applications. Explainable artificial intelligence (XAI) aims to help human decision-makers in understanding the operation of such complex ML models, thus eliciting trust in their operation. Unfortunately, the majority of past XAI work is based on informal approaches, that offer no guarantees of rigor. Unsurprisingly, there exists comprehensive experimental and theoretical evidence confirming that informal methods of XAI can provide human-decision makers with erroneous information. Logic-based XAI represents a rigorous approach to explainability; it is model-based and offers the strongest guarantees of rigor of computed explanations. However, a well-known drawback of logic-based XAI is the complexity of logic reasoning, especially for highly complex ML models. Recent work proposed distance-restricted explanations, i.e. explanations that are rigorous provided the distance to a given input is small enough. Distance-restricted explainability is tightly related with adversarial robustness, and it has been shown to scale for moderately complex ML models, but the number of inputs still represents a key limiting factor. This paper investigates novel algorithms for scaling up the performance of logic-based explainers when computing and enumerating ML model explanations with a large number of inputs.

Anytime Approximate Formal Feature Attribution

Widespread use of artificial intelligence (AI) algorithms and machine learning (ML) models on the one hand and a number of crucial issues pertaining to them warrant the need for explainable artificial intelligence (XAI). A key explainability question is: given this decision was made, what are the input features which contributed to the decision? Although a range of XAI approaches exist to tackle this problem, most of them have significant limitations. Heuristic XAI approaches suffer from the lack of quality guarantees, and often try to approximate Shapley values, which is not the same as explaining which features contribute to a decision. A recent alternative is so-called formal feature attribution (FFA), which defines feature importance as the fraction of formal abductive explanations (AXp's) containing the given feature. This measures feature importance from the view of formally reasoning about the model's behavior. It is challenging to compute FFA using its definition because that involves counting AXp's, although one can approximate it. Based on these results, this paper makes several contributions. First, it gives compelling evidence that computing FFA is intractable, even if the set of contrastive formal explanations (CXp's) is provided, by proving that the problem is #P-hard. Second, by using the duality between AXp's and CXp's, it proposes an efficient heuristic to switch from CXp enumeration to AXp enumeration on-the-fly resulting in an adaptive explanation enumeration algorithm effectively approximating FFA in an anytime fashion. Finally, experimental results obtained on a range of widely used datasets demonstrate the effectiveness of the proposed FFA approximation approach in terms of the error of FFA approximation as well as the number of explanations computed and their diversity given a fixed time limit.

On Formal Feature Attribution and Its Approximation

Recent years have witnessed the widespread use of artificial intelligence (AI) algorithms and machine learning (ML) models. Despite their tremendous success, a number of vital problems like ML model brittleness, their fairness, and the lack of interpretability warrant the need for the active developments in explainable artificial intelligence (XAI) and formal ML model verification. The two major lines of work in XAI include feature selection methods, e.g. Anchors, and feature attribution techniques, e.g. LIME and SHAP. Despite their promise, most of the existing feature selection and attribution approaches are susceptible to a range of critical issues, including explanation unsoundness and out-of-distribution sampling. A recent formal approach to XAI (FXAI) although serving as an alternative to the above and free of these issues suffers from a few other limitations. For instance and besides the scalability limitation, the formal approach is unable to tackle the feature attribution problem. Additionally, a formal explanation despite being formally sound is typically quite large, which hampers its applicability in practical settings. Motivated by the above, this paper proposes a way to apply the apparatus of formal XAI to the case of feature attribution based on formal explanation enumeration. Formal feature attribution (FFA) is argued to be advantageous over the existing methods, both formal and non-formal. Given the practical complexity of the problem, the paper then proposes an efficient technique for approximating exact FFA. Finally, it offers experimental evidence of the effectiveness of the proposed approximate FFA in comparison to the existing feature attribution algorithms not only in terms of feature importance and but also in terms of their relative order.

Delivering Inflated Explanations

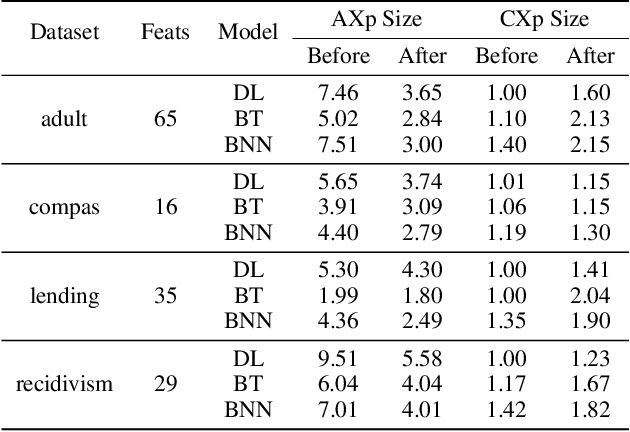
In the quest for Explainable Artificial Intelligence (XAI) one of the questions that frequently arises given a decision made by an AI system is, ``why was the decision made in this way?'' Formal approaches to explainability build a formal model of the AI system and use this to reason about the properties of the system. Given a set of feature values for an instance to be explained, and a resulting decision, a formal abductive explanation is a set of features, such that if they take the given value will always lead to the same decision. This explanation is useful, it shows that only some features were used in making the final decision. But it is narrow, it only shows that if the selected features take their given values the decision is unchanged. It's possible that some features may change values and still lead to the same decision. In this paper we formally define inflated explanations which is a set of features, and for each feature of set of values (always including the value of the instance being explained), such that the decision will remain unchanged. Inflated explanations are more informative than abductive explanations since e.g they allow us to see if the exact value of a feature is important, or it could be any nearby value. Overall they allow us to better understand the role of each feature in the decision. We show that we can compute inflated explanations for not that much greater cost than abductive explanations, and that we can extend duality results for abductive explanations also to inflated explanations.

On Computing Probabilistic Abductive Explanations

The most widely studied explainable AI (XAI) approaches are unsound. This is the case with well-known model-agnostic explanation approaches, and it is also the case with approaches based on saliency maps. One solution is to consider intrinsic interpretability, which does not exhibit the drawback of unsoundness. Unfortunately, intrinsic interpretability can display unwieldy explanation redundancy. Formal explainability represents the alternative to these non-rigorous approaches, with one example being PI-explanations. Unfortunately, PI-explanations also exhibit important drawbacks, the most visible of which is arguably their size. Recently, it has been observed that the (absolute) rigor of PI-explanations can be traded off for a smaller explanation size, by computing the so-called relevant sets. Given some positive {\delta}, a set S of features is {\delta}-relevant if, when the features in S are fixed, the probability of getting the target class exceeds {\delta}. However, even for very simple classifiers, the complexity of computing relevant sets of features is prohibitive, with the decision problem being NPPP-complete for circuit-based classifiers. In contrast with earlier negative results, this paper investigates practical approaches for computing relevant sets for a number of widely used classifiers that include Decision Trees (DTs), Naive Bayes Classifiers (NBCs), and several families of classifiers obtained from propositional languages. Moreover, the paper shows that, in practice, and for these families of classifiers, relevant sets are easy to compute. Furthermore, the experiments confirm that succinct sets of relevant features can be obtained for the families of classifiers considered.

Eliminating The Impossible, Whatever Remains Must Be True

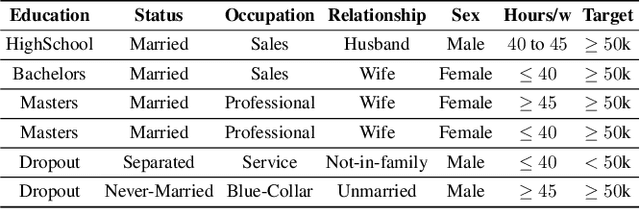
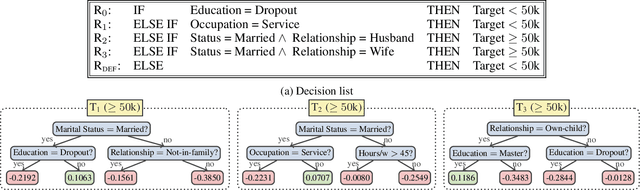
The rise of AI methods to make predictions and decisions has led to a pressing need for more explainable artificial intelligence (XAI) methods. One common approach for XAI is to produce a post-hoc explanation, explaining why a black box ML model made a certain prediction. Formal approaches to post-hoc explanations provide succinct reasons for why a prediction was made, as well as why not another prediction was made. But these approaches assume that features are independent and uniformly distributed. While this means that "why" explanations are correct, they may be longer than required. It also means the "why not" explanations may be suspect as the counterexamples they rely on may not be meaningful. In this paper, we show how one can apply background knowledge to give more succinct "why" formal explanations, that are presumably easier to interpret by humans, and give more accurate "why not" explanations. Furthermore, we also show how to use existing rule induction techniques to efficiently extract background information from a dataset, and also how to report which background information was used to make an explanation, allowing a human to examine it if they doubt the correctness of the explanation.

On Tackling Explanation Redundancy in Decision Trees

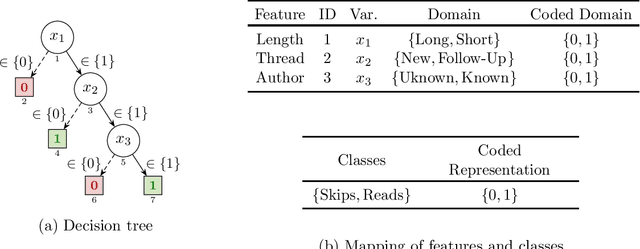
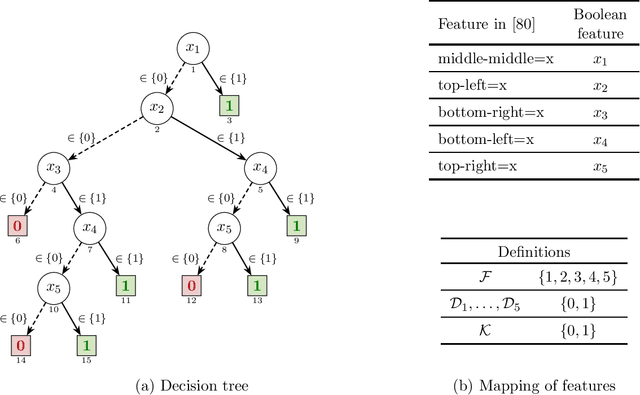
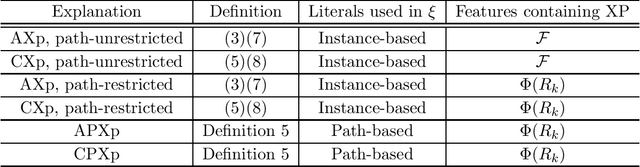
Decision trees (DTs) epitomize the ideal of interpretability of machine learning (ML) models. The interpretability of decision trees motivates explainability approaches by so-called intrinsic interpretability, and it is at the core of recent proposals for applying interpretable ML models in high-risk applications. The belief in DT interpretability is justified by the fact that explanations for DT predictions are generally expected to be succinct. Indeed, in the case of DTs, explanations correspond to DT paths. Since decision trees are ideally shallow, and so paths contain far fewer features than the total number of features, explanations in DTs are expected to be succinct, and hence interpretable. This paper offers both theoretical and experimental arguments demonstrating that, as long as interpretability of decision trees equates with succinctness of explanations, then decision trees ought not be deemed interpretable. The paper introduces logically rigorous path explanations and path explanation redundancy, and proves that there exist functions for which decision trees must exhibit paths with arbitrarily large explanation redundancy. The paper also proves that only a very restricted class of functions can be represented with DTs that exhibit no explanation redundancy. In addition, the paper includes experimental results substantiating that path explanation redundancy is observed ubiquitously in decision trees, including those obtained using different tree learning algorithms, but also in a wide range of publicly available decision trees. The paper also proposes polynomial-time algorithms for eliminating path explanation redundancy, which in practice require negligible time to compute. Thus, these algorithms serve to indirectly attain irreducible, and so succinct, explanations for decision trees.