Distributed Link Sparsification for Scalable Scheduling Using Graph Neural Networks

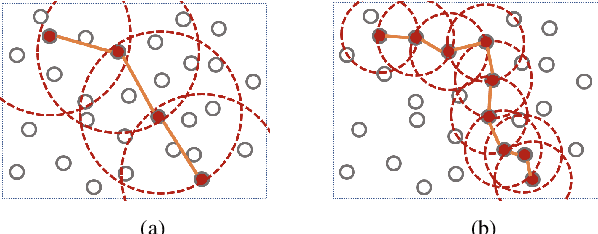
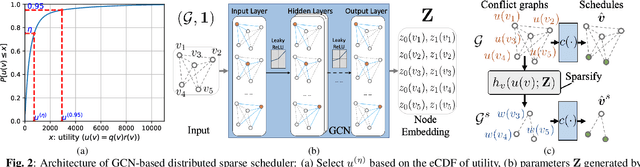
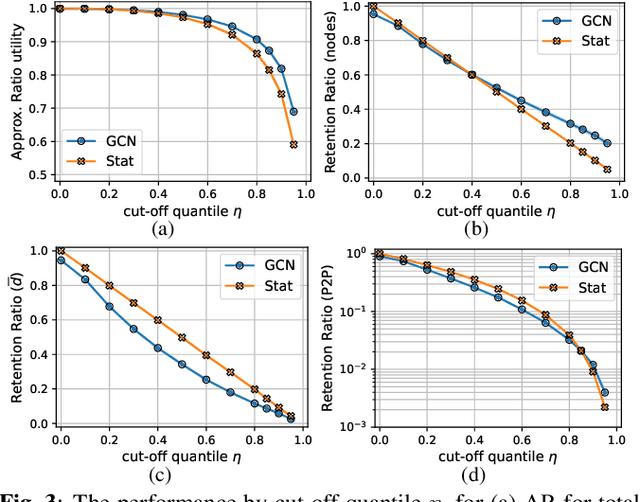
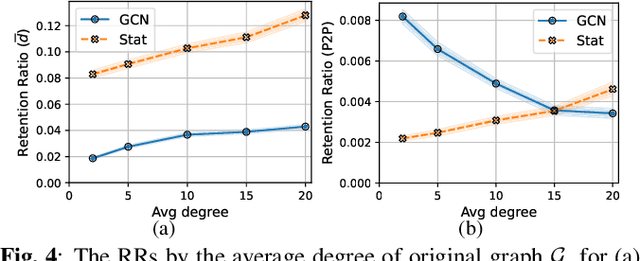
Distributed scheduling algorithms for throughput or utility maximization in dense wireless multi-hop networks can have overwhelmingly high overhead, causing increased congestion, energy consumption, radio footprint, and security vulnerability. For wireless networks with dense connectivity, we propose a distributed scheme for link sparsification with graph convolutional networks (GCNs), which can reduce the scheduling overhead while keeping most of the network capacity. In a nutshell, a trainable GCN module generates node embeddings as topology-aware and reusable parameters for a local decision mechanism, based on which a link can withdraw itself from the scheduling contention if it is not likely to win. In medium-sized wireless networks, our proposed sparse scheduler beats classical threshold-based sparsification policies by retaining almost $70\%$ of the total capacity achieved by a distributed greedy max-weight scheduler with $0.4\%$ of the point-to-point message complexity and $2.6\%$ of the average number of interfering neighbors per link.

Detection by Sampling: Massive MIMO Detector based on Langevin Dynamics

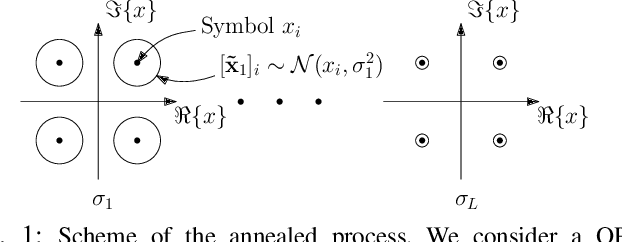
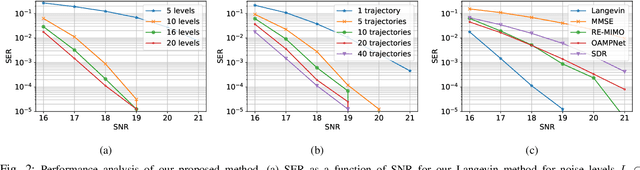
Optimal symbol detection in multiple-input multiple-output (MIMO) systems is known to be an NP-hard problem. Hence, the objective of any detector of practical relevance is to get reasonably close to the optimal solution while keeping the computational complexity in check. In this work, we propose a MIMO detector based on an annealed version of Langevin (stochastic) dynamics. More precisely, we define a stochastic dynamical process whose stationary distribution coincides with the posterior distribution of the symbols given our observations. In essence, this allows us to approximate the maximum a posteriori estimator of the transmitted symbols by sampling from the proposed Langevin dynamic. Furthermore, we carefully craft this stochastic dynamic by gradually adding a sequence of noise with decreasing variance to the trajectories, which ensures that the estimated symbols belong to a pre-specified discrete constellation. Through numerical experiments, we show that our proposed detector yields state-of-the-art symbol error rate performance.

On Local Distributions in Graph Signal Processing

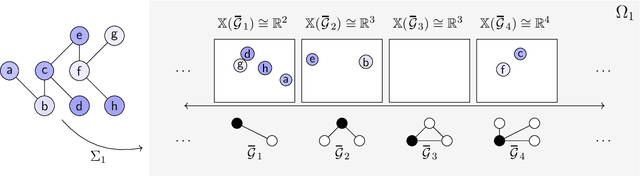
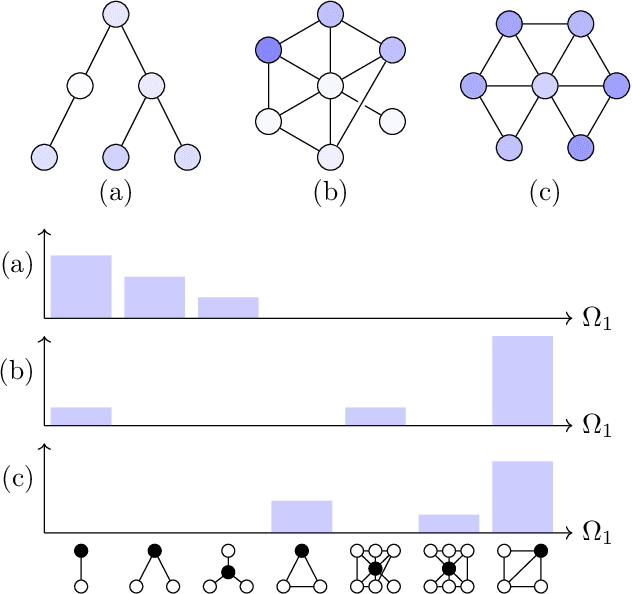
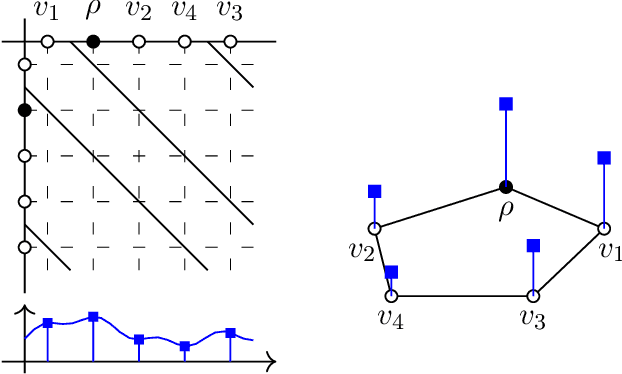
Graph filtering is the cornerstone operation in graph signal processing (GSP). Thus, understanding it is key in developing potent GSP methods. Graph filters are local and distributed linear operations, whose output depends only on the local neighborhood of each node. Moreover, a graph filter's output can be computed separately at each node by carrying out repeated exchanges with immediate neighbors. Graph filters can be compactly written as polynomials of a graph shift operator (typically, a sparse matrix description of the graph). This has led to relating the properties of the filters with the spectral properties of the corresponding matrix -- which encodes global structure of the graph. In this work, we propose a framework that relies solely on the local distribution of the neighborhoods of a graph. The crux of this approach is to describe graphs and graph signals in terms of a measurable space of rooted balls. Leveraging this, we are able to seamlessly compare graphs of different sizes and coming from different models, yielding results on the convergence of spectral densities, transferability of filters across arbitrary graphs, and continuity of graph signal properties with respect to the distribution of local substructures.

Graphon-aided Joint Estimation of Multiple Graphs

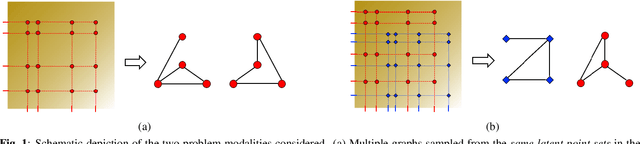
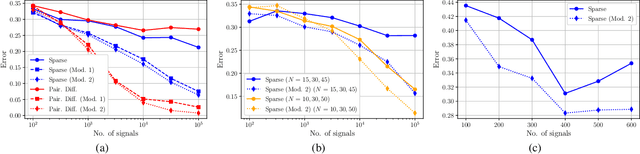
We consider the problem of estimating the topology of multiple networks from nodal observations, where these networks are assumed to be drawn from the same (unknown) random graph model. We adopt a graphon as our random graph model, which is a nonparametric model from which graphs of potentially different sizes can be drawn. The versatility of graphons allows us to tackle the joint inference problem even for the cases where the graphs to be recovered contain different number of nodes and lack precise alignment across the graphs. Our solution is based on combining a maximum likelihood penalty with graphon estimation schemes and can be used to augment existing network inference methods. We validate our proposed approach by comparing its performance against competing methods in synthetic and real-world datasets.

Graph-based Algorithm Unfolding for Energy-aware Power Allocation in Wireless Networks

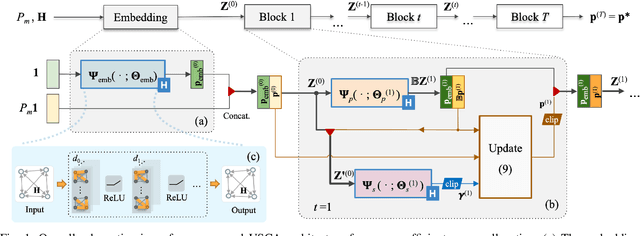
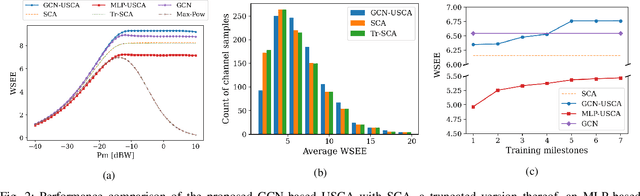
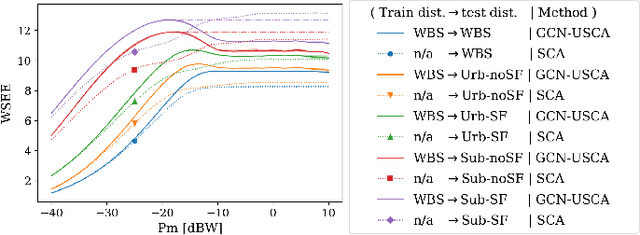
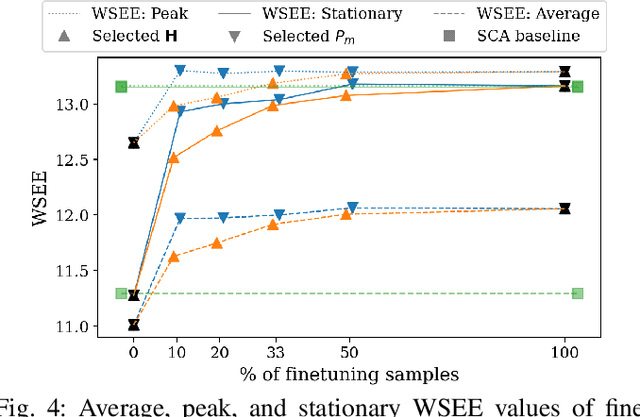
We develop a novel graph-based trainable framework to maximize the weighted sum energy efficiency (WSEE) for power allocation in wireless communication networks. To address the non-convex nature of the problem, the proposed method consists of modular structures inspired by a classical iterative suboptimal approach and enhanced with learnable components. More precisely, we propose a deep unfolding of the successive concave approximation (SCA) method. In our unfolded SCA (USCA) framework, the originally preset parameters are now learnable via graph convolutional neural networks (GCNs) that directly exploit multi-user channel state information as the underlying graph adjacency matrix. We show the permutation equivariance of the proposed architecture, which promotes generalizability across different network topologies of varying size, density, and channel distribution. The USCA framework is trained through a stochastic gradient descent approach using a progressive training strategy. The unsupervised loss is carefully devised to feature the monotonic property of the objective under maximum power constraints. Comprehensive numerical results demonstrate outstanding performance and robustness of USCA over state-of-the-art benchmarks.

Power Allocation for Wireless Federated Learning using Graph Neural Networks

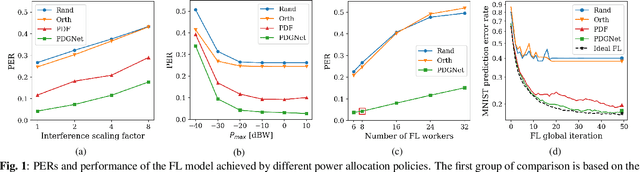
We propose a data-driven approach for power allocation in the context of federated learning (FL) over interference-limited wireless networks. The power policy is designed to maximize the transmitted information during the FL process under communication constraints, with the ultimate objective of improving the accuracy and efficiency of the global FL model being trained. The proposed power allocation policy is parameterized using a graph convolutional network and the associated constrained optimization problem is solved through a primal-dual algorithm. Numerical experiments show that the proposed method outperforms three baseline methods in both transmission success rate and FL global performance.

Delay-Oriented Distributed Scheduling Using Graph Neural Networks

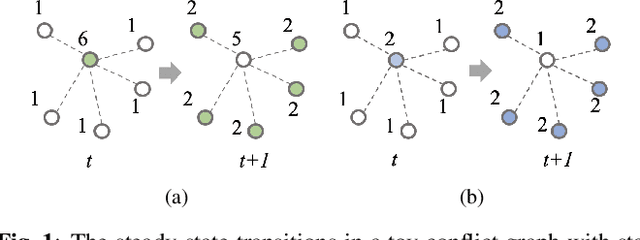
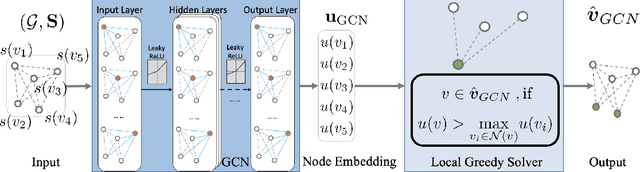
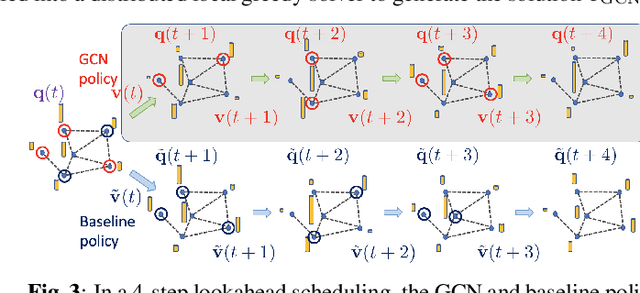
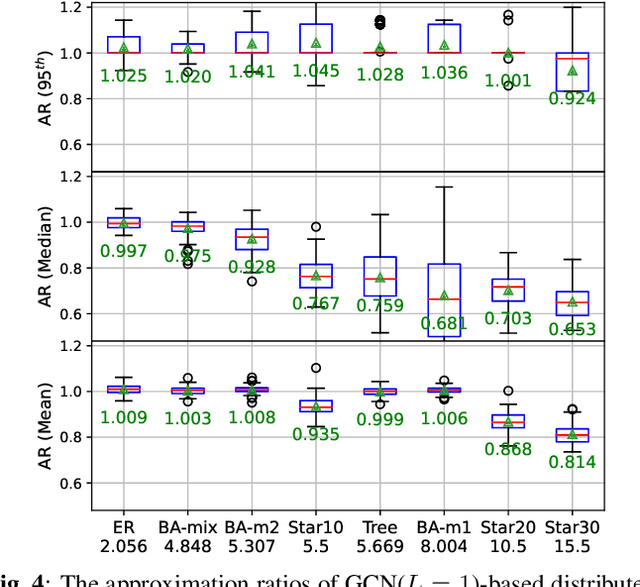
In wireless multi-hop networks, delay is an important metric for many applications. However, the max-weight scheduling algorithms in the literature typically focus on instantaneous optimality, in which the schedule is selected by solving a maximum weighted independent set (MWIS) problem on the interference graph at each time slot. These myopic policies perform poorly in delay-oriented scheduling, in which the dependency between the current backlogs of the network and the schedule of the previous time slot needs to be considered. To address this issue, we propose a delay-oriented distributed scheduler based on graph convolutional networks (GCNs). In a nutshell, a trainable GCN module generates node embeddings that capture the network topology as well as multi-step lookahead backlogs, before calling a distributed greedy MWIS solver. In small- to medium-sized wireless networks with heterogeneous transmit power, where a few central links have many interfering neighbors, our proposed distributed scheduler can outperform the myopic schedulers based on greedy and instantaneously optimal MWIS solvers, with good generalizability across graph models and minimal increase in communication complexity.

Stability Analysis of Unfolded WMMSE for Power Allocation

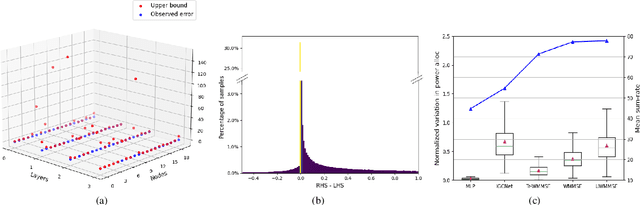
Power allocation is one of the fundamental problems in wireless networks and a wide variety of algorithms address this problem from different perspectives. A common element among these algorithms is that they rely on an estimation of the channel state, which may be inaccurate on account of hardware defects, noisy feedback systems, and environmental and adversarial disturbances. Therefore, it is essential that the output power allocation of these algorithms is stable with respect to input perturbations, to the extent that the variations in the output are bounded for bounded variations in the input. In this paper, we focus on UWMMSE -- a modern algorithm leveraging graph neural networks --, and illustrate its stability to additive input perturbations of bounded energy through both theoretical analysis and empirical validation.

Robust MIMO Detection using Hypernetworks with Learned Regularizers

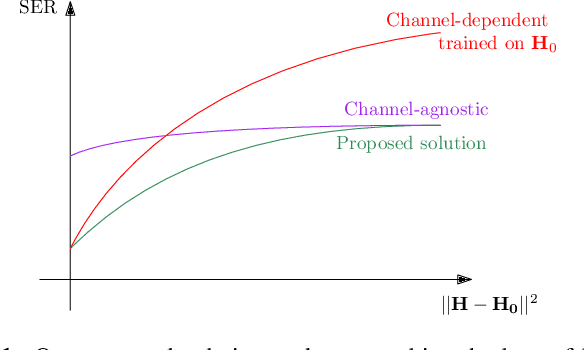
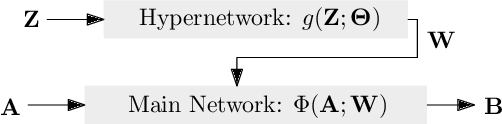
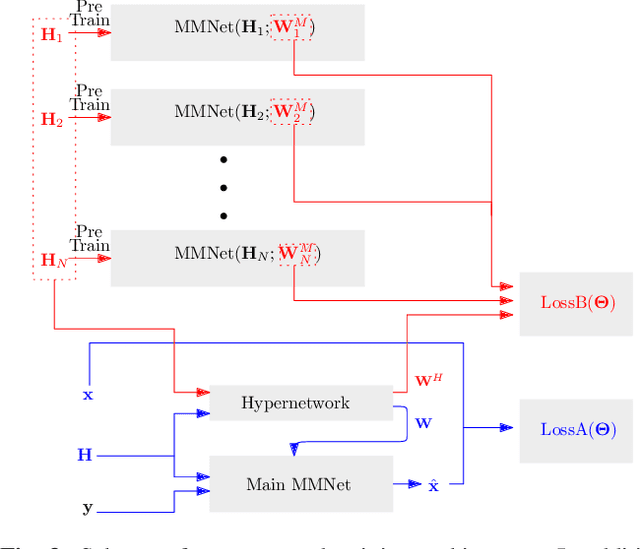
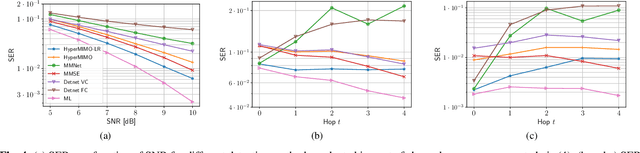
Optimal symbol detection in multiple-input multiple-output (MIMO) systems is known to be an NP-hard problem. Recently, there has been a growing interest to get reasonably close to the optimal solution using neural networks while keeping the computational complexity in check. However, existing work based on deep learning shows that it is difficult to design a generic network that works well for a variety of channels. In this work, we propose a method that tries to strike a balance between symbol error rate (SER) performance and generality of channels. Our method is based on hypernetworks that generate the parameters of a neural network-based detector that works well on a specific channel. We propose a general framework by regularizing the training of the hypernetwork with some pre-trained instances of the channel-specific method. Through numerical experiments, we show that our proposed method yields high performance for a set of prespecified channel realizations while generalizing well to all channels drawn from a specific distribution.

Label Propagation across Graphs: Node Classification using Graph Neural Tangent Kernels

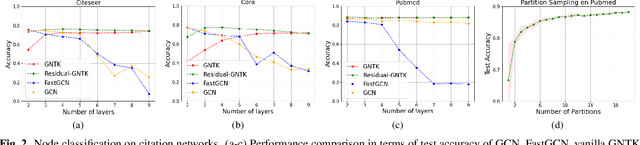
Graph neural networks (GNNs) have achieved superior performance on node classification tasks in the last few years. Commonly, this is framed in a transductive semi-supervised learning setup wherein the entire graph, including the target nodes to be labeled, is available for training. Driven in part by scalability, recent works have focused on the inductive case where only the labeled portion of a graph is available for training. In this context, our current work considers a challenging inductive setting where a set of labeled graphs are available for training while the unlabeled target graph is completely separate, i.e., there are no connections between labeled and unlabeled nodes. Under the implicit assumption that the testing and training graphs come from similar distributions, our goal is to develop a labeling function that generalizes to unobserved connectivity structures. To that end, we employ a graph neural tangent kernel (GNTK) that corresponds to infinitely wide GNNs to find correspondences between nodes in different graphs based on both the topology and the node features. We augment the capabilities of the GNTK with residual connections and empirically illustrate its performance gains on standard benchmarks.