Logical Distillation of Graph Neural Networks

We present a logic based interpretable model for learning on graphs and an algorithm to distill this model from a Graph Neural Network (GNN). Recent results have shown connections between the expressivity of GNNs and the two-variable fragment of first-order logic with counting quantifiers (C2). We introduce a decision-tree based model which leverages an extension of C2 to distill interpretable logical classifiers from GNNs. We test our approach on multiple GNN architectures. The distilled models are interpretable, succinct, and attain similar accuracy to the underlying GNN. Furthermore, when the ground truth is expressible in C2, our approach outperforms the GNN.

Understanding Domain-Size Generalization in Markov Logic Networks

We study the generalization behavior of Markov Logic Networks (MLNs) across relational structures of different sizes. Multiple works have noticed that MLNs learned on a given domain generalize poorly across domains of different sizes. This behavior emerges from a lack of internal consistency within an MLN when used across different domain sizes. In this paper, we quantify this inconsistency and bound it in terms of the variance of the MLN parameters. The parameter variance also bounds the KL divergence between an MLN's marginal distributions taken from different domain sizes. We use these bounds to show that maximizing the data log-likelihood while simultaneously minimizing the parameter variance corresponds to two natural notions of generalization across domain sizes. Our theoretical results apply to Exponential Random Graphs and other Markov network based relational models. Finally, we observe that solutions known to decrease the variance of the MLN parameters, like regularization and Domain-Size Aware MLNs, increase the internal consistency of the MLNs. We empirically verify our results on four different datasets, with different methods to control parameter variance, showing that controlling parameter variance leads to better generalization.

Simple and Effective Transfer Learning for Neuro-Symbolic Integration

Deep Learning (DL) techniques have achieved remarkable successes in recent years. However, their ability to generalize and execute reasoning tasks remains a challenge. A potential solution to this issue is Neuro-Symbolic Integration (NeSy), where neural approaches are combined with symbolic reasoning. Most of these methods exploit a neural network to map perceptions to symbols and a logical reasoner to predict the output of the downstream task. These methods exhibit superior generalization capacity compared to fully neural architectures. However, they suffer from several issues, including slow convergence, learning difficulties with complex perception tasks, and convergence to local minima. This paper proposes a simple yet effective method to ameliorate these problems. The key idea involves pretraining a neural model on the downstream task. Then, a NeSy model is trained on the same task via transfer learning, where the weights of the perceptual part are injected from the pretrained network. The key observation of our work is that the neural network fails to generalize only at the level of the symbolic part while being perfectly capable of learning the mapping from perceptions to symbols. We have tested our training strategy on various SOTA NeSy methods and datasets, demonstrating consistent improvements in the aforementioned problems.

Lifted Inference beyond First-Order Logic

Weighted First Order Model Counting (WFOMC) is fundamental to probabilistic inference in statistical relational learning models. As WFOMC is known to be intractable in general ($\#$P-complete), logical fragments that admit polynomial time WFOMC are of significant interest. Such fragments are called domain liftable. Recent works have shown that the two-variable fragment of first order logic extended with counting quantifiers ($\mathrm{C^2}$) is domain-liftable. However, many properties of real-world data, like acyclicity in citation networks and connectivity in social networks, cannot be modeled in $\mathrm{C^2}$, or first order logic in general. In this work, we expand the domain liftability of $\mathrm{C^2}$ with multiple such properties. We show that any $\mathrm{C^2}$ sentence remains domain liftable when one of its relations is restricted to represent a directed acyclic graph, a connected graph, a tree (resp. a directed tree) or a forest (resp. a directed forest). All our results rely on a novel and general methodology of "counting by splitting". Besides their application to probabilistic inference, our results provide a general framework for counting combinatorial structures. We expand a vast array of previous results in discrete mathematics literature on directed acyclic graphs, phylogenetic networks, etc.

Weighted First Order Model Counting with Directed Acyclic Graph Axioms

Weighted First Order Model Counting (WFOMC) is the task of computing the weighted sum of the models of a first-order logic sentence. Probabilistic inference problems in many statistical relational learning frameworks can be cast as a WFOMC problem. However, in general, WFOMC is known to be intractable (#P_1- complete). Hence, logical fragments that admit polynomial time WFOMC are of significant interest. Such fragments are called domain liftable. Recent works have identified the two-variable fragment of first-order logic, extended with counting quantifiers, to be domain liftable. In this paper, we extend this fragment with a Directed Acyclic Graph axiom, i.e., a relation is interpreted as a Directed Acyclic Graph.

Deep Symbolic Learning: Discovering Symbols and Rules from Perceptions

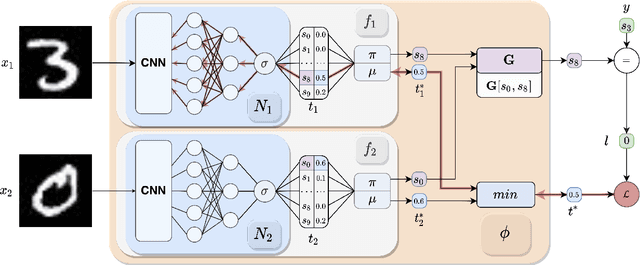
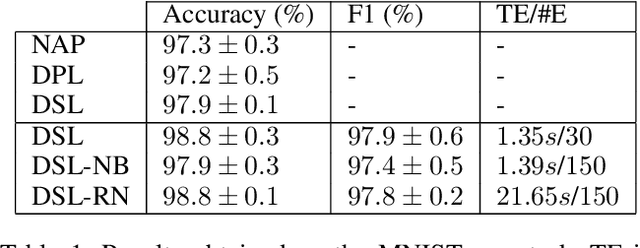
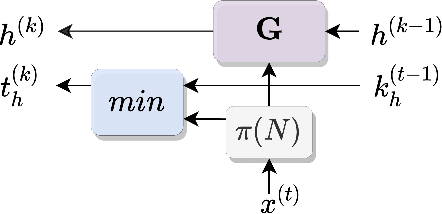
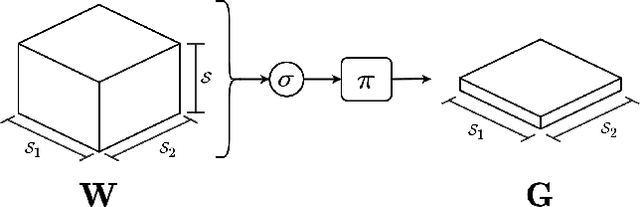
Neuro-Symbolic (NeSy) integration combines symbolic reasoning with Neural Networks (NNs) for tasks requiring perception and reasoning. Most NeSy systems rely on continuous relaxation of logical knowledge and no discrete decisions are made within the model pipeline. Furthermore, these methods assume that the symbolic rules are given. In this paper, we propose Deep Symbolic Learning (DSL), a NeSy system that learns NeSy-functions, i.e., the composition of a (set of) perception functions which map continuous data to discrete symbols, and a symbolic function over the set of symbols. DSL learns simultaneously the perception and symbolic functions, while being trained only on their composition (NeSy-function). The key novelty of DSL is that it can create internal (interpretable) symbolic representations and map them to perception inputs within a differentiable NN learning pipeline. The created symbols are automatically selected to generate symbolic functions that best explain the data. We provide experimental analysis to substantiate the efficacy of DSL in simultaneously learning perception and symbolic functions.

On Projectivity in Markov Logic Networks

Markov Logic Networks (MLNs) define a probability distribution on relational structures over varying domain sizes. Many works have noticed that MLNs, like many other relational models, do not admit consistent marginal inference over varying domain sizes. Furthermore, MLNs learnt on a certain domain do not generalize to new domains of varied sizes. In recent works, connections have emerged between domain size dependence, lifted inference and learning from sub-sampled domains. The central idea to these works is the notion of projectivity. The probability distributions ascribed by projective models render the marginal probabilities of sub-structures independent of the domain cardinality. Hence, projective models admit efficient marginal inference, removing any dependence on the domain size. Furthermore, projective models potentially allow efficient and consistent parameter learning from sub-sampled domains. In this paper, we characterize the necessary and sufficient conditions for a two-variable MLN to be projective. We then isolate a special model in this class of MLNs, namely Relational Block Model (RBM). We show that, in terms of data likelihood maximization, RBM is the best possible projective MLN in the two-variable fragment. Finally, we show that RBMs also admit consistent parameter learning over sub-sampled domains.

Weighted Model Counting in FO2 with Cardinality Constraints and Counting Quantifiers: A Closed Form Formula

Weighted First-Order Model Counting (WFOMC) computes the weighted sum of the models of a first-order logic theory on a given finite domain. First-Order Logic theories that admit polynomial-time WFOMC w.r.t domain cardinality are called domain liftable. We introduce the concept of lifted interpretations as a tool for formulating closed-forms for WFOMC. Using lifted interpretations, we reconstruct the closed-form formula for polynomial-time FOMC in the universally quantified fragment of FO2, earlier proposed by Beame et al. We then expand this closed-form to incorporate cardinality constraints, existential quantifiers, and counting quantifiers (a.k.a C2) without losing domain-liftability. Finally, we show that the obtained closed-form motivates a natural definition of a family of weight functions strictly larger than symmetric weight functions.