Differentiable Programming for Computational Plasma Physics

Differentiable programming allows for derivatives of functions implemented via computer code to be calculated automatically. These derivatives are calculated using automatic differentiation (AD). This thesis explores two applications of differentiable programming to computational plasma physics. First, we consider how differentiable programming can be used to simplify and improve stellarator optimization. We introduce a stellarator coil design code (FOCUSADD) that uses gradient-based optimization to produce stellarator coils with finite build. Because we use reverse mode AD, which can compute gradients of scalar functions with the same computational complexity as the function, FOCUSADD is simple, flexible, and efficient. We then discuss two additional applications of AD in stellarator optimization. Second, we explore how machine learning (ML) can be used to improve or replace the numerical methods used to solve partial differential equations (PDEs), focusing on time-dependent PDEs in fluid mechanics relevant to plasma physics. Differentiable programming allows neural networks and other techniques from ML to be embedded within numerical methods. This is a promising, but relatively new, research area. We focus on two basic questions. First, can we design ML-based PDE solvers that have the same guarantees of conservation, stability, and positivity that standard numerical methods do? The answer is yes; we introduce error-correcting algorithms that preserve invariants of time-dependent PDEs. Second, which types of ML-based solvers work best at solving PDEs? We perform a systematic review of the scientific literature on solving PDEs with ML. Unfortunately we discover two issues, weak baselines and reporting biases, that affect the interpretation reproducibility of a significant majority of published research. We conclude that using ML to solve PDEs is not as promising as we initially believed.

Weak baselines and reporting biases lead to overoptimism in machine learning for fluid-related partial differential equations

One of the most promising applications of machine learning (ML) in computational physics is to accelerate the solution of partial differential equations (PDEs). The key objective of ML-based PDE solvers is to output a sufficiently accurate solution faster than standard numerical methods, which are used as a baseline comparison. We first perform a systematic review of the ML-for-PDE solving literature. Of articles that use ML to solve a fluid-related PDE and claim to outperform a standard numerical method, we determine that 79% (60/76) compare to a weak baseline. Second, we find evidence that reporting biases, especially outcome reporting bias and publication bias, are widespread. We conclude that ML-for-PDE solving research is overoptimistic: weak baselines lead to overly positive results, while reporting biases lead to underreporting of negative results. To a large extent, these issues appear to be caused by factors similar to those of past reproducibility crises: researcher degrees of freedom and a bias towards positive results. We call for bottom-up cultural changes to minimize biased reporting as well as top-down structural reforms intended to reduce perverse incentives for doing so.

Invariant preservation in machine learned PDE solvers via error correction

Machine learned partial differential equation (PDE) solvers trade the reliability of standard numerical methods for potential gains in accuracy and/or speed. The only way for a solver to guarantee that it outputs the exact solution is to use a convergent method in the limit that the grid spacing $\Delta x$ and timestep $\Delta t$ approach zero. Machine learned solvers, which learn to update the solution at large $\Delta x$ and/or $\Delta t$, can never guarantee perfect accuracy. Some amount of error is inevitable, so the question becomes: how do we constrain machine learned solvers to give us the sorts of errors that we are willing to tolerate? In this paper, we design more reliable machine learned PDE solvers by preserving discrete analogues of the continuous invariants of the underlying PDE. Examples of such invariants include conservation of mass, conservation of energy, the second law of thermodynamics, and/or non-negative density. Our key insight is simple: to preserve invariants, at each timestep apply an error-correcting algorithm to the update rule. Though this strategy is different from how standard solvers preserve invariants, it is necessary to retain the flexibility that allows machine learned solvers to be accurate at large $\Delta x$ and/or $\Delta t$. This strategy can be applied to any autoregressive solver for any time-dependent PDE in arbitrary geometries with arbitrary boundary conditions. Although this strategy is very general, the specific error-correcting algorithms need to be tailored to the invariants of the underlying equations as well as to the solution representation and time-stepping scheme of the solver. The error-correcting algorithms we introduce have two key properties. First, by preserving the right invariants they guarantee numerical stability. Second, in closed or periodic systems they do so without degrading the accuracy of an already-accurate solver.

Meta-PDE: Learning to Solve PDEs Quickly Without a Mesh

Partial differential equations (PDEs) are often computationally challenging to solve, and in many settings many related PDEs must be be solved either at every timestep or for a variety of candidate boundary conditions, parameters, or geometric domains. We present a meta-learning based method which learns to rapidly solve problems from a distribution of related PDEs. We use meta-learning (MAML and LEAP) to identify initializations for a neural network representation of the PDE solution such that a residual of the PDE can be quickly minimized on a novel task. We apply our meta-solving approach to a nonlinear Poisson's equation, 1D Burgers' equation, and hyperelasticity equations with varying parameters, geometries, and boundary conditions. The resulting Meta-PDE method finds qualitatively accurate solutions to most problems within a few gradient steps; for the nonlinear Poisson and hyper-elasticity equation this results in an intermediate accuracy approximation up to an order of magnitude faster than a baseline finite element analysis (FEA) solver with equivalent accuracy. In comparison to other learned solvers and surrogate models, this meta-learning approach can be trained without supervision from expensive ground-truth data, does not require a mesh, and can even be used when the geometry and topology varies between tasks.

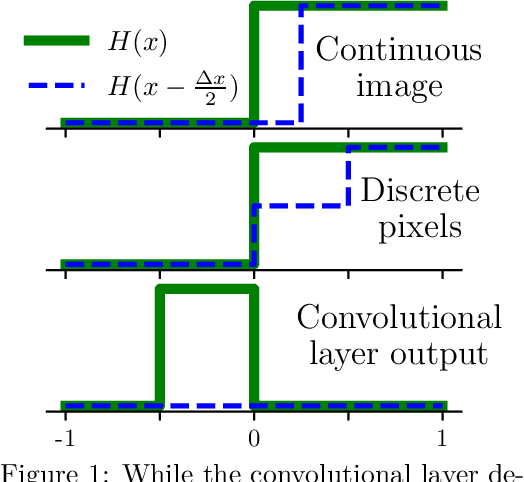
Convolutional Layers Are Not Translation Equivariant

The purpose of this paper is to correct a misconception about convolutional neural networks (CNNs). CNNs are made up of convolutional layers which are shift equivariant due to weight sharing. However, contrary to popular belief, convolutional layers are not translation equivariant, even when boundary effects are ignored and when pooling and subsampling are absent. This is because shift equivariance is a discrete symmetry while translation equivariance is a continuous symmetry. That discrete systems do not in general inherit continuous equivariances is a fundamental limitation of equivariant deep learning. We discuss two implications of this fact. First, CNNs have achieved success in image processing despite not inheriting the translation equivariance of the physical systems they model. Second, using CNNs to solve partial differential equations (PDEs) will not result in translation equivariant solvers.

Randomized Automatic Differentiation

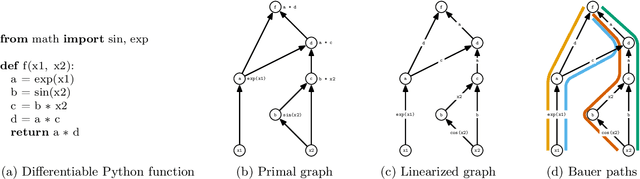
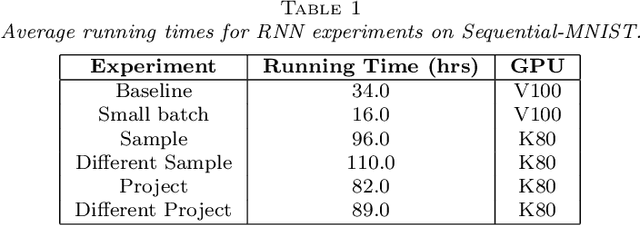
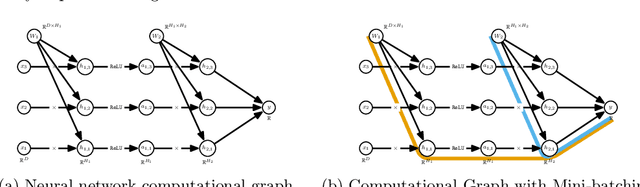
The successes of deep learning, variational inference, and many other fields have been aided by specialized implementations of reverse-mode automatic differentiation (AD) to compute gradients of mega-dimensional objectives. The AD techniques underlying these tools were designed to compute exact gradients to numerical precision, but modern machine learning models are almost always trained with stochastic gradient descent. Why spend computation and memory on exact (minibatch) gradients only to use them for stochastic optimization? We develop a general framework and approach for randomized automatic differentiation (RAD), which allows unbiased gradient estimates to be computed with reduced memory in return for variance. We examine limitations of the general approach, and argue that we must leverage problem specific structure to realize benefits. We develop RAD techniques for a variety of simple neural network architectures, and show that for a fixed memory budget, RAD converges in fewer iterations than using a small batch size for feedforward networks, and in a similar number for recurrent networks. We also show that RAD can be applied to scientific computing, and use it to develop a low-memory stochastic gradient method for optimizing the control parameters of a linear reaction-diffusion PDE representing a fission reactor.