A Uniform Confidence Phenomenon in Deep Learning and its Implications for Calibration

Despite the impressive generalization capabilities of deep neural networks, they have been repeatedly shown to poorly estimate their predictive uncertainty - in other words, they are frequently overconfident when they are wrong. Fixing this issue is known as model calibration, and has consequently received much attention in the form of modified training schemes and post-training calibration procedures. In this work, we present a significant hurdle to the calibration of modern models: deep neural networks have large neighborhoods of almost certain confidence around their training points. We demonstrate in our experiments that this phenomenon consistently arises (in the context of image classification) across many model and dataset pairs. Furthermore, we prove that when this phenomenon holds, for a large class of data distributions with overlaps between classes, it is not possible to obtain a model that is asymptotically better than random (with respect to calibration) even after applying the standard post-training calibration technique of temperature scaling. On the other hand, we also prove that it is possible to circumvent this defect by changing the training process to use a modified loss based on the Mixup data augmentation technique.

Smoothing the Landscape Boosts the Signal for SGD: Optimal Sample Complexity for Learning Single Index Models

We focus on the task of learning a single index model $\sigma(w^\star \cdot x)$ with respect to the isotropic Gaussian distribution in $d$ dimensions. Prior work has shown that the sample complexity of learning $w^\star$ is governed by the information exponent $k^\star$ of the link function $\sigma$, which is defined as the index of the first nonzero Hermite coefficient of $\sigma$. Ben Arous et al. (2021) showed that $n \gtrsim d^{k^\star-1}$ samples suffice for learning $w^\star$ and that this is tight for online SGD. However, the CSQ lower bound for gradient based methods only shows that $n \gtrsim d^{k^\star/2}$ samples are necessary. In this work, we close the gap between the upper and lower bounds by showing that online SGD on a smoothed loss learns $w^\star$ with $n \gtrsim d^{k^\star/2}$ samples. We also draw connections to statistical analyses of tensor PCA and to the implicit regularization effects of minibatch SGD on empirical losses.

Depth Separation with Multilayer Mean-Field Networks

Depth separation -- why a deeper network is more powerful than a shallower one -- has been a major problem in deep learning theory. Previous results often focus on representation power. For example, arXiv:1904.06984 constructed a function that is easy to approximate using a 3-layer network but not approximable by any 2-layer network. In this paper, we show that this separation is in fact algorithmic: one can learn the function constructed by arXiv:1904.06984 using an overparameterized network with polynomially many neurons efficiently. Our result relies on a new way of extending the mean-field limit to multilayer networks, and a decomposition of loss that factors out the error introduced by the discretization of infinite-width mean-field networks.

Do Transformers Parse while Predicting the Masked Word?

Pre-trained language models have been shown to encode linguistic structures, e.g. dependency and constituency parse trees, in their embeddings while being trained on unsupervised loss functions like masked language modeling. Some doubts have been raised whether the models actually are doing parsing or only some computation weakly correlated with it. We study questions: (a) Is it possible to explicitly describe transformers with realistic embedding dimension, number of heads, etc. that are capable of doing parsing -- or even approximate parsing? (b) Why do pre-trained models capture parsing structure? This paper takes a step toward answering these questions in the context of generative modeling with PCFGs. We show that masked language models like BERT or RoBERTa of moderate sizes can approximately execute the Inside-Outside algorithm for the English PCFG [Marcus et al, 1993]. We also show that the Inside-Outside algorithm is optimal for masked language modeling loss on the PCFG-generated data. We also give a construction of transformers with $50$ layers, $15$ attention heads, and $1275$ dimensional embeddings in average such that using its embeddings it is possible to do constituency parsing with $>70\%$ F1 score on PTB dataset. We conduct probing experiments on models pre-trained on PCFG-generated data to show that this not only allows recovery of approximate parse tree, but also recovers marginal span probabilities computed by the Inside-Outside algorithm, which suggests an implicit bias of masked language modeling towards this algorithm.

Hiding Data Helps: On the Benefits of Masking for Sparse Coding

Sparse coding refers to modeling a signal as sparse linear combinations of the elements of a learned dictionary. Sparse coding has proven to be a successful and interpretable approach in many applications, such as signal processing, computer vision, and medical imaging. While this success has spurred much work on sparse coding with provable guarantees, work on the setting where the learned dictionary is larger (or \textit{over-realized}) with respect to the ground truth is comparatively nascent. Existing theoretical results in the over-realized regime are limited to the case of noise-less data. In this paper, we show that for over-realized sparse coding in the presence of noise, minimizing the standard dictionary learning objective can fail to recover the ground-truth dictionary, regardless of the magnitude of the signal in the data-generating process. Furthermore, drawing from the growing body of work on self-supervised learning, we propose a novel masking objective and we prove that minimizing this new objective can recover the ground-truth dictionary. We corroborate our theoretical results with experiments across several parameter regimes, showing that our proposed objective enjoys better empirical performance than the standard reconstruction objective.

Implicit Regularization Leads to Benign Overfitting for Sparse Linear Regression

In deep learning, often the training process finds an interpolator (a solution with 0 training loss), but the test loss is still low. This phenomenon, known as benign overfitting, is a major mystery that received a lot of recent attention. One common mechanism for benign overfitting is implicit regularization, where the training process leads to additional properties for the interpolator, often characterized by minimizing certain norms. However, even for a simple sparse linear regression problem $y = \beta^{*\top} x +\xi$ with sparse $\beta^*$, neither minimum $\ell_1$ or $\ell_2$ norm interpolator gives the optimal test loss. In this work, we give a different parametrization of the model which leads to a new implicit regularization effect that combines the benefit of $\ell_1$ and $\ell_2$ interpolators. We show that training our new model via gradient descent leads to an interpolator with near-optimal test loss. Our result is based on careful analysis of the training dynamics and provides another example of implicit regularization effect that goes beyond norm minimization.

Provably Learning Diverse Features in Multi-View Data with Midpoint Mixup

Mixup is a data augmentation technique that relies on training using random convex combinations of data points and their labels. In recent years, Mixup has become a standard primitive used in the training of state-of-the-art image classification models due to its demonstrated benefits over empirical risk minimization with regards to generalization and robustness. In this work, we try to explain some of this success from a feature learning perspective. We focus our attention on classification problems in which each class may have multiple associated features (or views) that can be used to predict the class correctly. Our main theoretical results demonstrate that, for a non-trivial class of data distributions with two features per class, training a 2-layer convolutional network using empirical risk minimization can lead to learning only one feature for almost all classes while training with a specific instantiation of Mixup succeeds in learning both features for every class. We also show empirically that these theoretical insights extend to the practical settings of image benchmarks modified to have additional synthetic features.

Understanding Edge-of-Stability Training Dynamics with a Minimalist Example

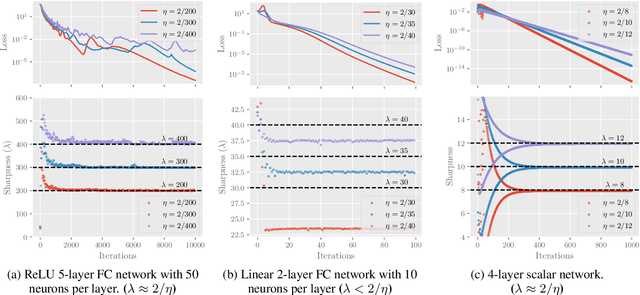
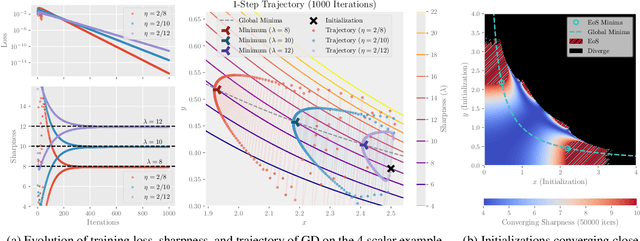
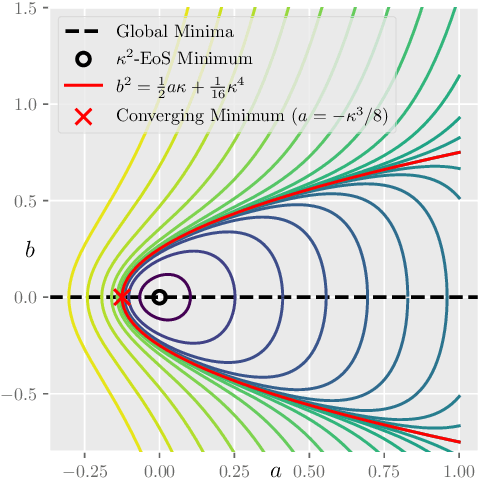
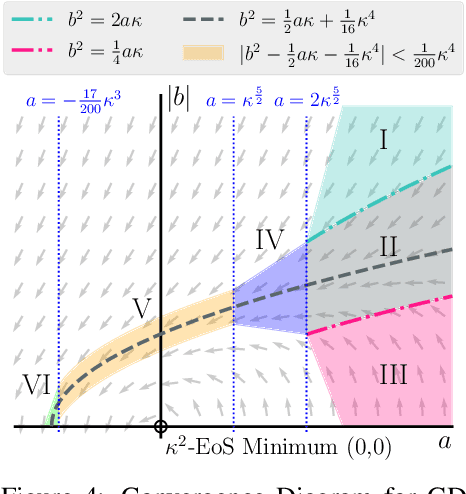
Recently, researchers observed that gradient descent for deep neural networks operates in an ``edge-of-stability'' (EoS) regime: the sharpness (maximum eigenvalue of the Hessian) is often larger than stability threshold 2/$\eta$ (where $\eta$ is the step size). Despite this, the loss oscillates and converges in the long run, and the sharpness at the end is just slightly below $2/\eta$. While many other well-understood nonconvex objectives such as matrix factorization or two-layer networks can also converge despite large sharpness, there is often a larger gap between sharpness of the endpoint and $2/\eta$. In this paper, we study EoS phenomenon by constructing a simple function that has the same behavior. We give rigorous analysis for its training dynamics in a large local region and explain why the final converging point has sharpness close to $2/\eta$. Globally we observe that the training dynamics for our example has an interesting bifurcating behavior, which was also observed in the training of neural nets.

Plateau in Monotonic Linear Interpolation -- A "Biased" View of Loss Landscape for Deep Networks

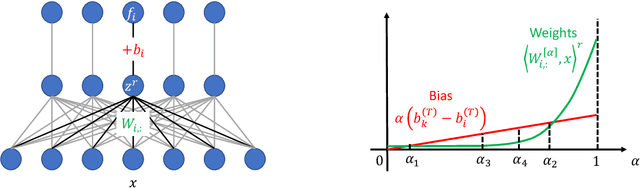
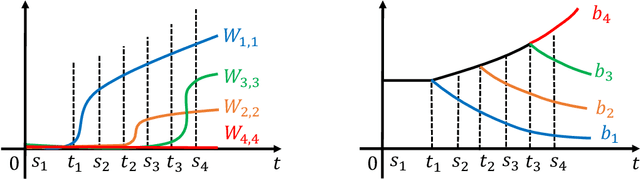
Monotonic linear interpolation (MLI) - on the line connecting a random initialization with the minimizer it converges to, the loss and accuracy are monotonic - is a phenomenon that is commonly observed in the training of neural networks. Such a phenomenon may seem to suggest that optimization of neural networks is easy. In this paper, we show that the MLI property is not necessarily related to the hardness of optimization problems, and empirical observations on MLI for deep neural networks depend heavily on biases. In particular, we show that interpolating both weights and biases linearly leads to very different influences on the final output, and when different classes have different last-layer biases on a deep network, there will be a long plateau in both the loss and accuracy interpolation (which existing theory of MLI cannot explain). We also show how the last-layer biases for different classes can be different even on a perfectly balanced dataset using a simple model. Empirically we demonstrate that similar intuitions hold on practical networks and realistic datasets.

A Regression Approach to Learning-Augmented Online Algorithms

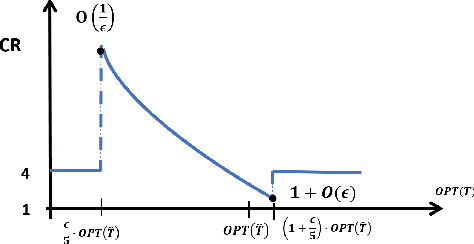
The emerging field of learning-augmented online algorithms uses ML techniques to predict future input parameters and thereby improve the performance of online algorithms. Since these parameters are, in general, real-valued functions, a natural approach is to use regression techniques to make these predictions. We introduce this approach in this paper, and explore it in the context of a general online search framework that captures classic problems like (generalized) ski rental, bin packing, minimum makespan scheduling, etc. We show nearly tight bounds on the sample complexity of this regression problem, and extend our results to the agnostic setting. From a technical standpoint, we show that the key is to incorporate online optimization benchmarks in the design of the loss function for the regression problem, thereby diverging from the use of off-the-shelf regression tools with standard bounds on statistical error.