Efficient nonmyopic Bayesian optimization and quadrature

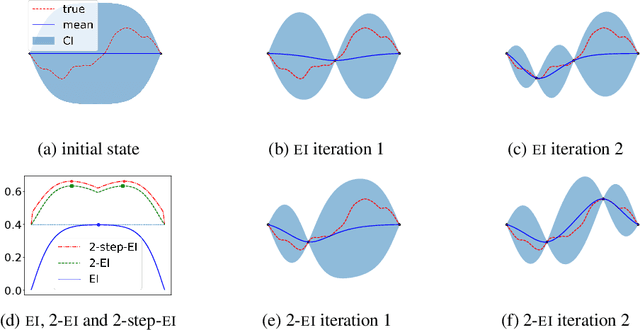
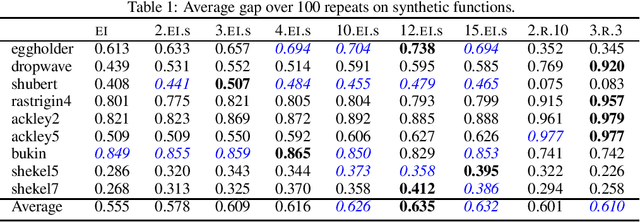
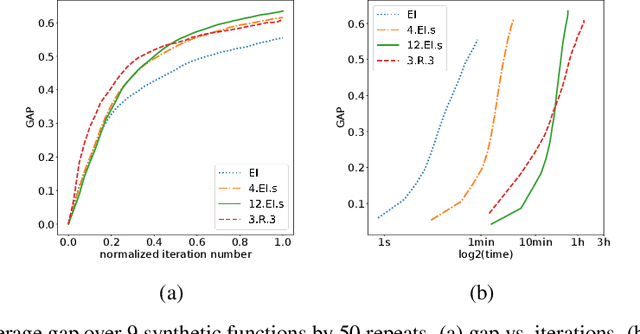
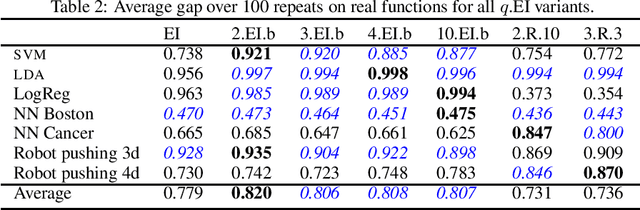
Finite-horizon sequential decision problems arise naturally in many machine learning contexts, including Bayesian optimization and Bayesian quadrature. Computing the optimal policy for such problems requires solving Bellman equations, which are generally intractable. Most existing work resorts to myopic approximations by limiting the decision horizon to only a single time-step, which can perform poorly at balancing exploration and exploitation. We propose a general framework for efficient, nonmyopic approximation of the optimal policy by drawing a connection between the optimal adaptive policy and its non-adaptive counterpart. Our proposal is to compute an optimal batch of points, then select a single point from within this batch to evaluate. We realize this idea for both Bayesian optimization and Bayesian quadrature and demonstrate that our proposed method significantly outperforms common myopic alternatives on a variety of tasks.

D-VAE: A Variational Autoencoder for Directed Acyclic Graphs

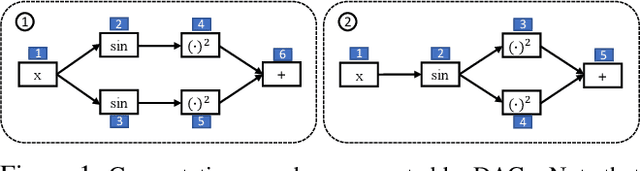
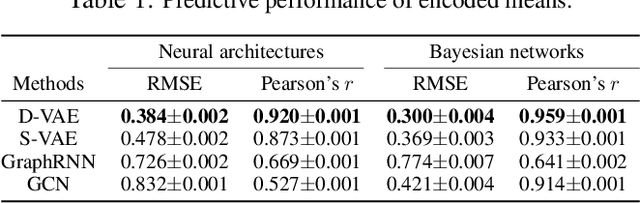
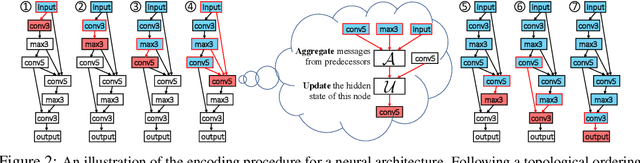
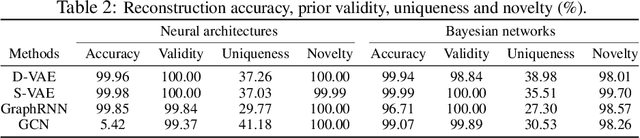
Graph structured data are abundant in the real world. Among different graph types, directed acyclic graphs (DAGs) are of particular interest to machine learning researchers, as many machine learning models are realized as computations on DAGs, including neural networks and Bayesian networks. In this paper, we study deep generative models for DAGs, and propose a novel DAG variational autoencoder (D-VAE). To encode DAGs into the latent space, we leverage graph neural networks. We propose an asynchronous message passing scheme that allows encoding the computations on DAGs, rather than using existing simultaneous message passing schemes to encode local graph structures. We demonstrate the effectiveness of our proposed D-VAE through two tasks: neural architecture search and Bayesian network structure learning. Experiments show that our model not only generates novel and valid DAGs, but also produces a smooth latent space that facilitates searching for DAGs with better performance through Bayesian optimization.

Automated Model Selection with Bayesian Quadrature

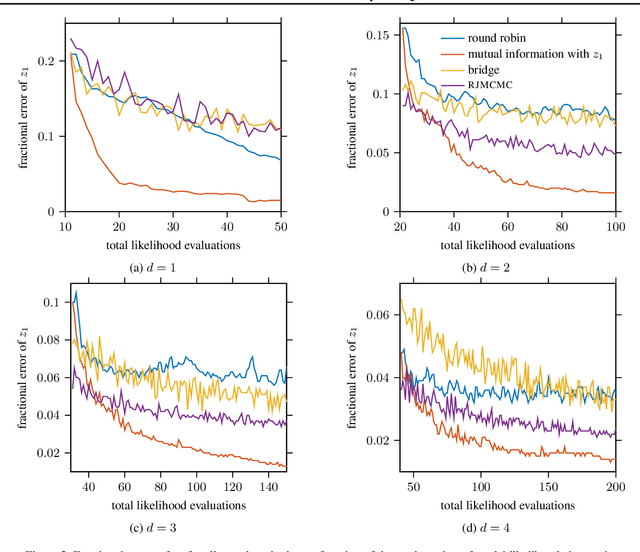
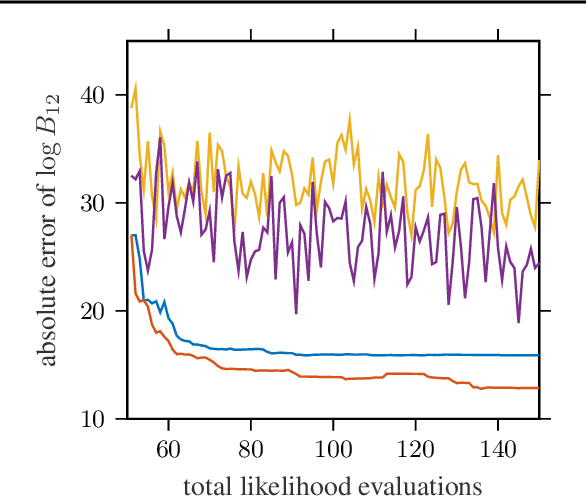
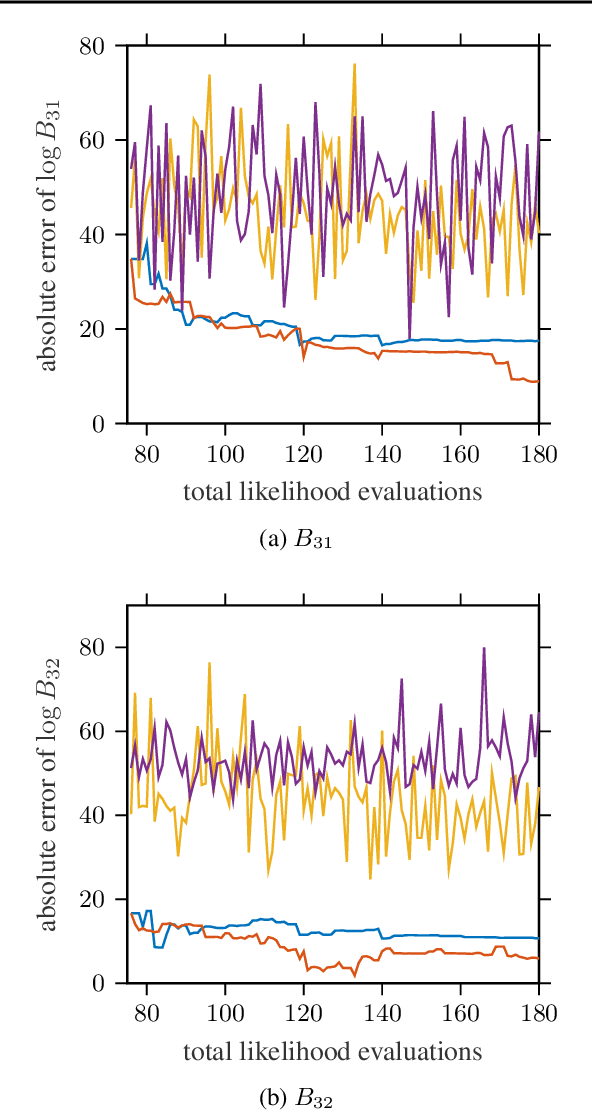
We present a novel technique for tailoring Bayesian quadrature (BQ) to model selection. The state-of-the-art for comparing the evidence of multiple models relies on Monte Carlo methods, which converge slowly and are unreliable for computationally expensive models. Previous research has shown that BQ offers sample efficiency superior to Monte Carlo in computing the evidence of an individual model. However, applying BQ directly to model comparison may waste computation producing an overly-accurate estimate for the evidence of a clearly poor model. We propose an automated and efficient algorithm for computing the most-relevant quantity for model selection: the posterior probability of a model. Our technique maximizes the mutual information between this quantity and observations of the models' likelihoods, yielding efficient acquisition of samples across disparate model spaces when likelihood observations are limited. Our method produces more-accurate model posterior estimates using fewer model likelihood evaluations than standard Bayesian quadrature and Monte Carlo estimators, as we demonstrate on synthetic and real-world examples.

Efficient nonmyopic active search with applications in drug and materials discovery

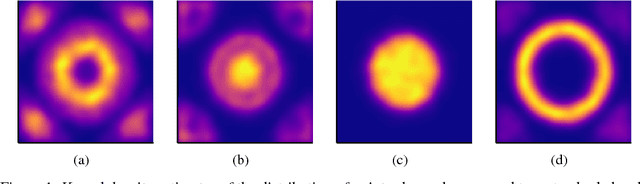
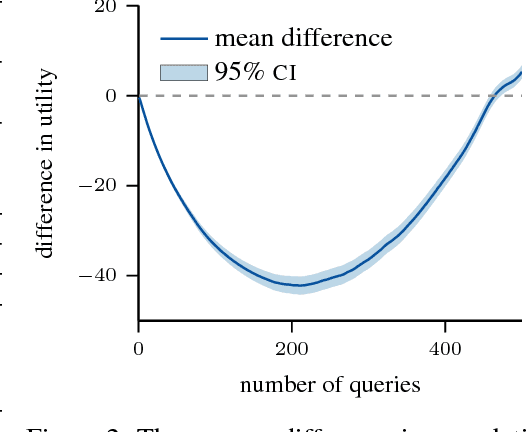
Active search is a learning paradigm for actively identifying as many members of a given class as possible. A critical target scenario is high-throughput screening for scientific discovery, such as drug or materials discovery. In this paper, we approach this problem in Bayesian decision framework. We first derive the Bayesian optimal policy under a natural utility, and establish a theoretical hardness of active search, proving that the optimal policy can not be approximated for any constant ratio. We also study the batch setting for the first time, where a batch of $b>1$ points can be queried at each iteration. We give an asymptotic lower bound, linear in batch size, on the adaptivity gap: how much we could lose if we query $b$ points at a time for $t$ iterations, instead of one point at a time for $bt$ iterations. We then introduce a novel approach to nonmyopic approximations of the optimal policy that admits efficient computation. Our proposed policy can automatically trade off exploration and exploitation, without relying on any tuning parameters. We also generalize our policy to batch setting, and propose two approaches to tackle the combinatorial search challenge. We evaluate our proposed policies on a large database of drug discovery and materials science. Results demonstrate the superior performance of our proposed policy in both sequential and batch setting; the nonmyopic behavior is also illustrated in various aspects.

Improving Quadrature for Constrained Integrands

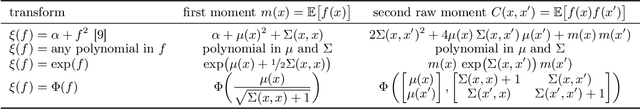
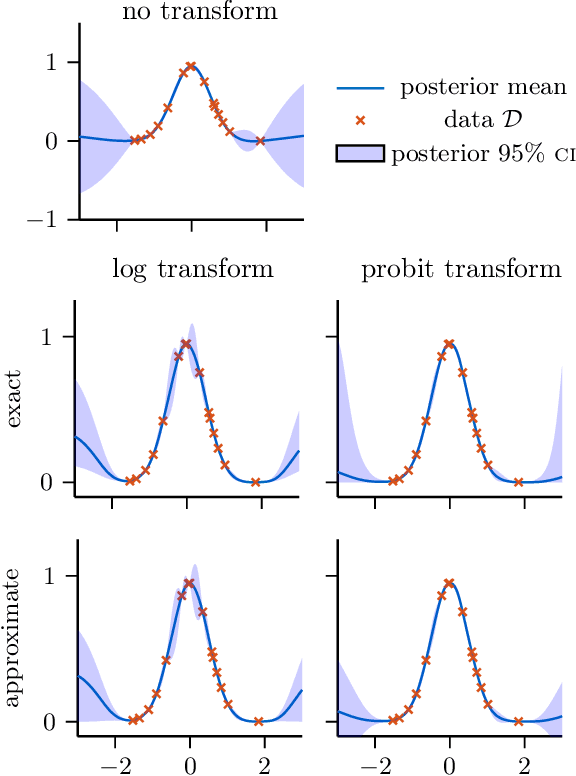
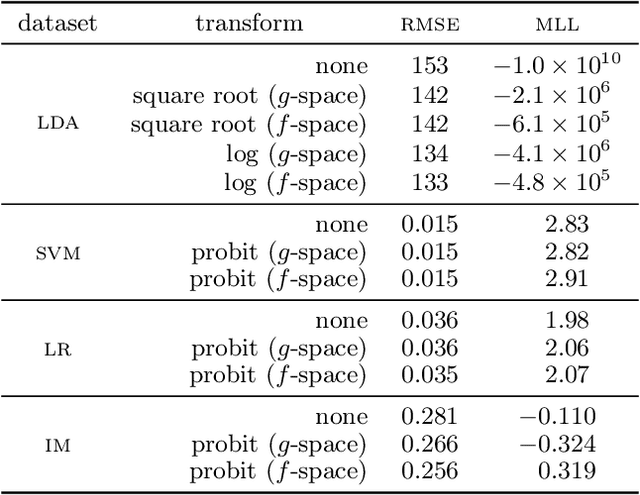
We present an improved Bayesian framework for performing inference of affine transformations of constrained functions. We focus on quadrature with nonnegative functions, a common task in Bayesian inference. We consider constraints on the range of the function of interest, such as nonnegativity or boundedness. Although our framework is general, we derive explicit approximation schemes for these constraints, and argue for the use of a log transformation for functions with high dynamic range such as likelihood surfaces. We propose a novel method for optimizing hyperparameters in this framework: we optimize the marginal likelihood in the original space, as opposed to in the transformed space. The result is a model that better explains the actual data. Experiments on synthetic and real-world data demonstrate our framework achieves superior estimates using less wall-clock time than existing Bayesian quadrature procedures.

Exact Sampling from Determinantal Point Processes

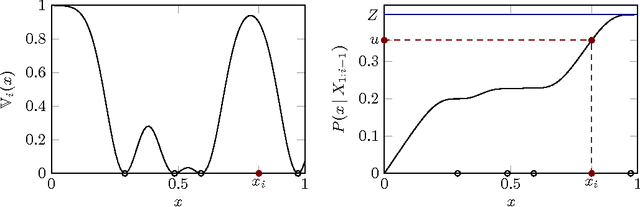
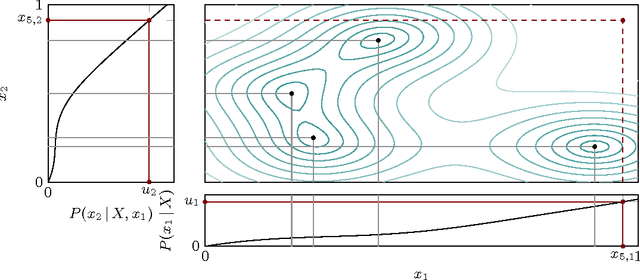
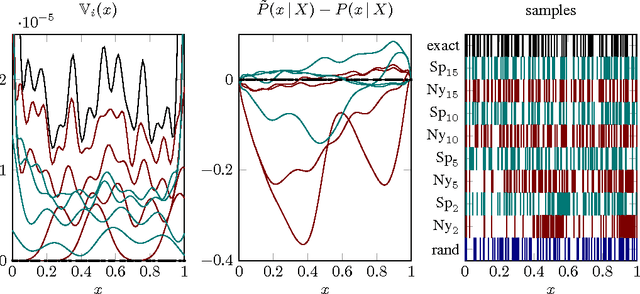
Determinantal point processes (DPPs) are an important concept in random matrix theory and combinatorics. They have also recently attracted interest in the study of numerical methods for machine learning, as they offer an elegant "missing link" between independent Monte Carlo sampling and deterministic evaluation on regular grids, applicable to a general set of spaces. This is helpful whenever an algorithm explores to reduce uncertainty, such as in active learning, Bayesian optimization, reinforcement learning, and marginalization in graphical models. To draw samples from a DPP in practice, existing literature focuses on approximate schemes of low cost, or comparably inefficient exact algorithms like rejection sampling. We point out that, for many settings of relevance to machine learning, it is also possible to draw exact samples from DPPs on continuous domains. We start from an intuitive example on the real line, which is then generalized to multivariate real vector spaces. We also compare to previously studied approximations, showing that exact sampling, despite higher cost, can be preferable where precision is needed.

Active Search for Sparse Signals with Region Sensing

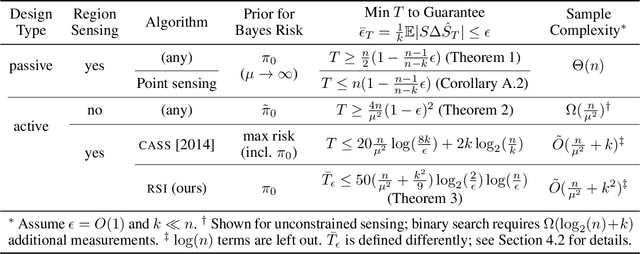
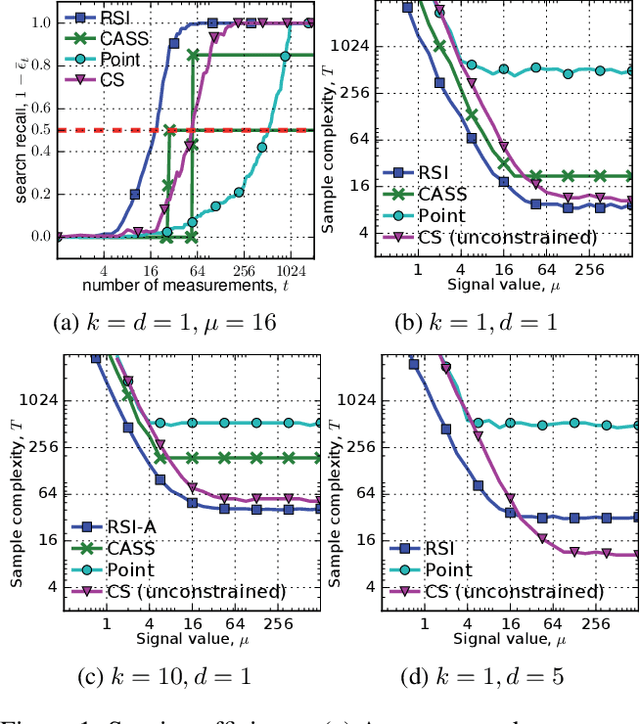
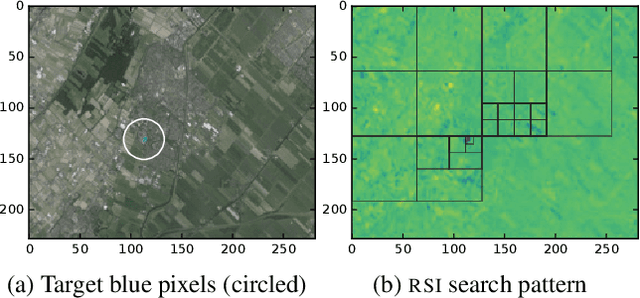
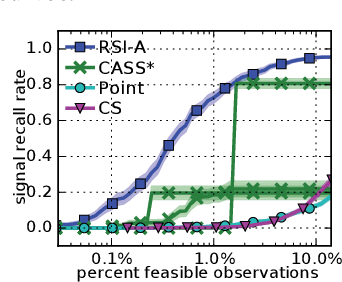
Autonomous systems can be used to search for sparse signals in a large space; e.g., aerial robots can be deployed to localize threats, detect gas leaks, or respond to distress calls. Intuitively, search algorithms may increase efficiency by collecting aggregate measurements summarizing large contiguous regions. However, most existing search methods either ignore the possibility of such region observations (e.g., Bayesian optimization and multi-armed bandits) or make strong assumptions about the sensing mechanism that allow each measurement to arbitrarily encode all signals in the entire environment (e.g., compressive sensing). We propose an algorithm that actively collects data to search for sparse signals using only noisy measurements of the average values on rectangular regions (including single points), based on the greedy maximization of information gain. We analyze our algorithm in 1d and show that it requires $\tilde{O}(\frac{n}{\mu^2}+k^2)$ measurements to recover all of $k$ signal locations with small Bayes error, where $\mu$ and $n$ are the signal strength and the size of the search space, respectively. We also show that active designs can be fundamentally more efficient than passive designs with region sensing, contrasting with the results of Arias-Castro, Candes, and Davenport (2013). We demonstrate the empirical performance of our algorithm on a search problem using satellite image data and in high dimensions.

Anomaly Detection and Removal Using Non-Stationary Gaussian Processes

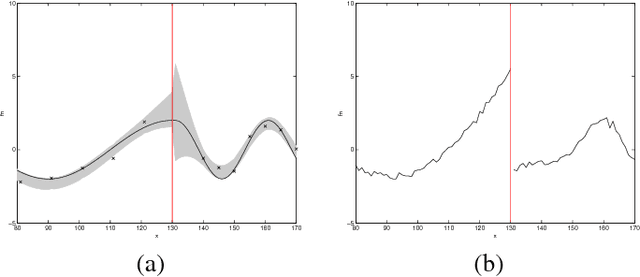
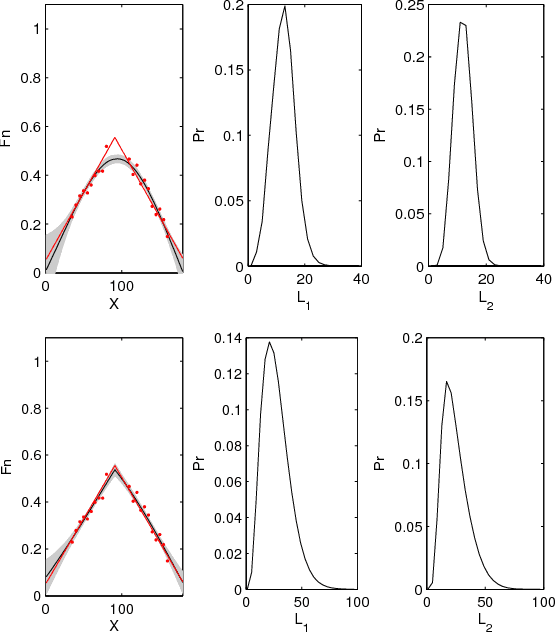
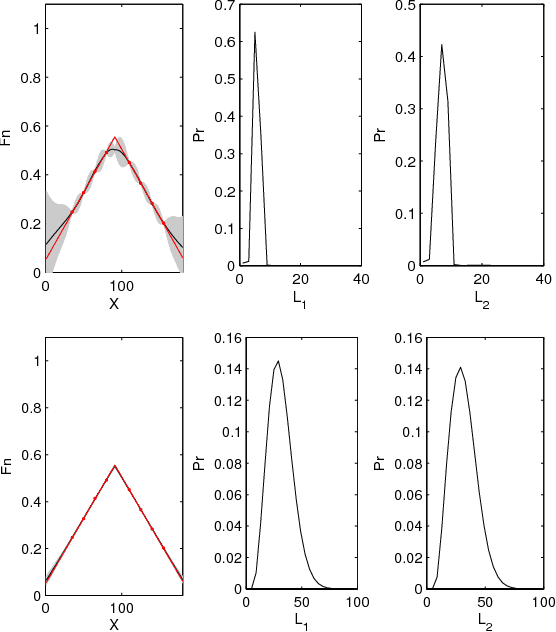
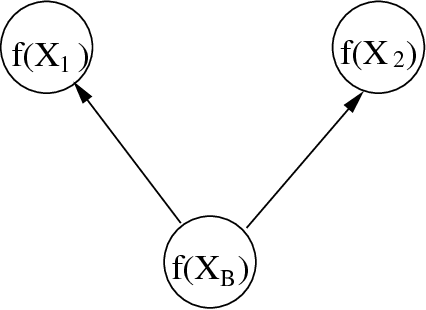
This paper proposes a novel Gaussian process approach to fault removal in time-series data. Fault removal does not delete the faulty signal data but, instead, massages the fault from the data. We assume that only one fault occurs at any one time and model the signal by two separate non-parametric Gaussian process models for both the physical phenomenon and the fault. In order to facilitate fault removal we introduce the Markov Region Link kernel for handling non-stationary Gaussian processes. This kernel is piece-wise stationary but guarantees that functions generated by it and their derivatives (when required) are everywhere continuous. We apply this kernel to the removal of drift and bias errors in faulty sensor data and also to the recovery of EOG artifact corrupted EEG signals.

Differentially Private Bayesian Optimization

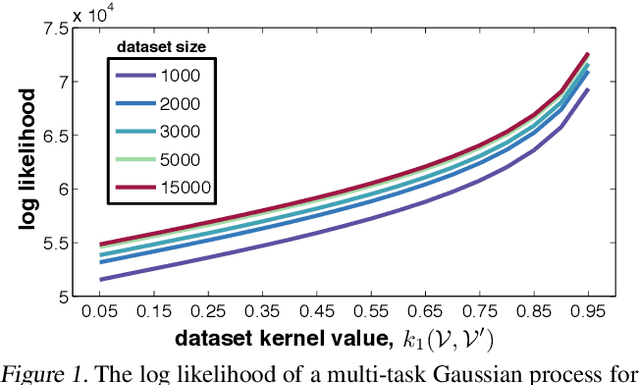
Bayesian optimization is a powerful tool for fine-tuning the hyper-parameters of a wide variety of machine learning models. The success of machine learning has led practitioners in diverse real-world settings to learn classifiers for practical problems. As machine learning becomes commonplace, Bayesian optimization becomes an attractive method for practitioners to automate the process of classifier hyper-parameter tuning. A key observation is that the data used for tuning models in these settings is often sensitive. Certain data such as genetic predisposition, personal email statistics, and car accident history, if not properly private, may be at risk of being inferred from Bayesian optimization outputs. To address this, we introduce methods for releasing the best hyper-parameters and classifier accuracy privately. Leveraging the strong theoretical guarantees of differential privacy and known Bayesian optimization convergence bounds, we prove that under a GP assumption these private quantities are also near-optimal. Finally, even if this assumption is not satisfied, we can use different smoothness guarantees to protect privacy.

Sampling for Inference in Probabilistic Models with Fast Bayesian Quadrature

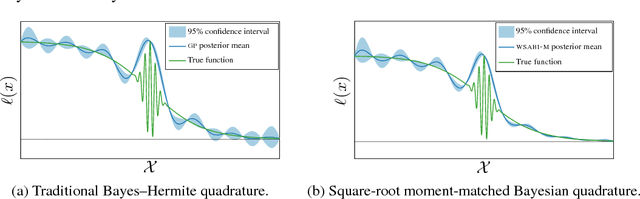
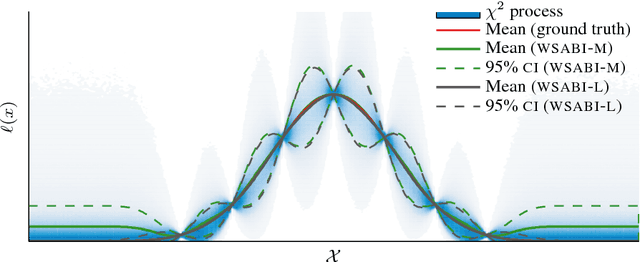
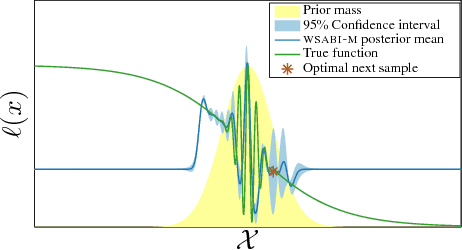
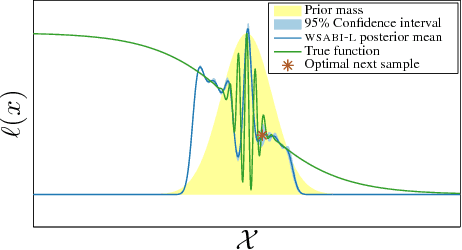
We propose a novel sampling framework for inference in probabilistic models: an active learning approach that converges more quickly (in wall-clock time) than Markov chain Monte Carlo (MCMC) benchmarks. The central challenge in probabilistic inference is numerical integration, to average over ensembles of models or unknown (hyper-)parameters (for example to compute the marginal likelihood or a partition function). MCMC has provided approaches to numerical integration that deliver state-of-the-art inference, but can suffer from sample inefficiency and poor convergence diagnostics. Bayesian quadrature techniques offer a model-based solution to such problems, but their uptake has been hindered by prohibitive computation costs. We introduce a warped model for probabilistic integrands (likelihoods) that are known to be non-negative, permitting a cheap active learning scheme to optimally select sample locations. Our algorithm is demonstrated to offer faster convergence (in seconds) relative to simple Monte Carlo and annealed importance sampling on both synthetic and real-world examples.