The Flip Side of the Reweighted Coin: Duality of Adaptive Dropout and Regularization

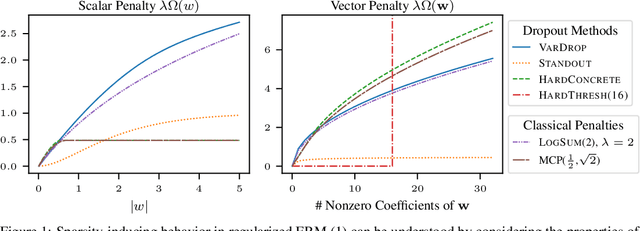
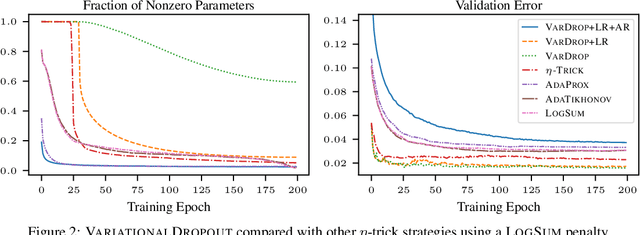
Among the most successful methods for sparsifying deep (neural) networks are those that adaptively mask the network weights throughout training. By examining this masking, or dropout, in the linear case, we uncover a duality between such adaptive methods and regularization through the so-called "$\eta$-trick" that casts both as iteratively reweighted optimizations. We show that any dropout strategy that adapts to the weights in a monotonic way corresponds to an effective subquadratic regularization penalty, and therefore leads to sparse solutions. We obtain the effective penalties for several popular sparsification strategies, which are remarkably similar to classical penalties commonly used in sparse optimization. Considering variational dropout as a case study, we demonstrate similar empirical behavior between the adaptive dropout method and classical methods on the task of deep network sparsification, validating our theory.

NePTuNe: Neural Powered Tucker Network for Knowledge Graph Completion

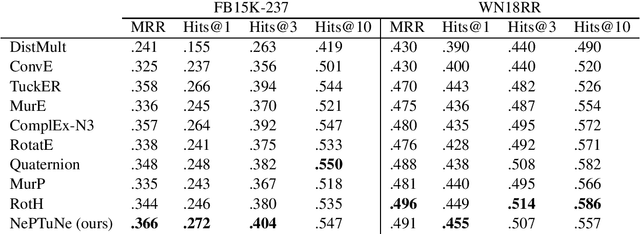
Knowledge graphs link entities through relations to provide a structured representation of real world facts. However, they are often incomplete, because they are based on only a small fraction of all plausible facts. The task of knowledge graph completion via link prediction aims to overcome this challenge by inferring missing facts represented as links between entities. Current approaches to link prediction leverage tensor factorization and/or deep learning. Factorization methods train and deploy rapidly thanks to their small number of parameters but have limited expressiveness due to their underlying linear methodology. Deep learning methods are more expressive but also computationally expensive and prone to overfitting due to their large number of trainable parameters. We propose Neural Powered Tucker Network (NePTuNe), a new hybrid link prediction model that couples the expressiveness of deep models with the speed and size of linear models. We demonstrate that NePTuNe provides state-of-the-art performance on the FB15K-237 dataset and near state-of-the-art performance on the WN18RR dataset.

Extreme Compressed Sensing of Poisson Rates from Multiple Measurements

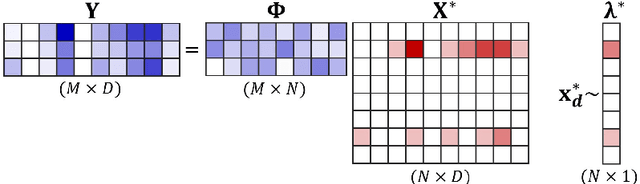
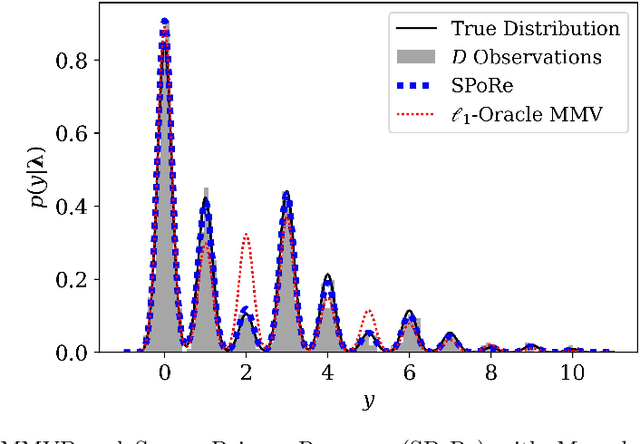
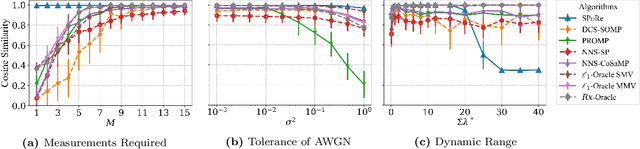
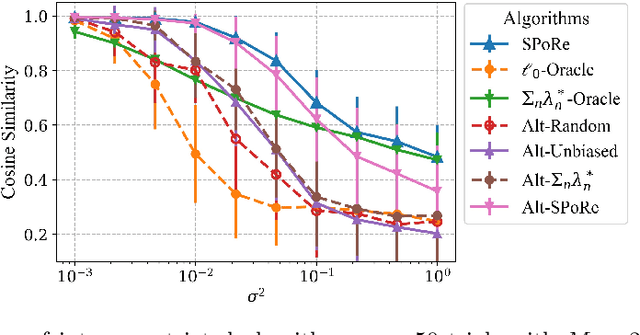
Compressed sensing (CS) is a signal processing technique that enables the efficient recovery of a sparse high-dimensional signal from low-dimensional measurements. In the multiple measurement vector (MMV) framework, a set of signals with the same support must be recovered from their corresponding measurements. Here, we present the first exploration of the MMV problem where signals are independently drawn from a sparse, multivariate Poisson distribution. We are primarily motivated by a suite of biosensing applications of microfluidics where analytes (such as whole cells or biomarkers) are captured in small volume partitions according to a Poisson distribution. We recover the sparse parameter vector of Poisson rates through maximum likelihood estimation with our novel Sparse Poisson Recovery (SPoRe) algorithm. SPoRe uses batch stochastic gradient ascent enabled by Monte Carlo approximations of otherwise intractable gradients. By uniquely leveraging the Poisson structure, SPoRe substantially outperforms a comprehensive set of existing and custom baseline CS algorithms. Notably, SPoRe can exhibit high performance even with one-dimensional measurements and high noise levels. This resource efficiency is not only unprecedented in the field of CS but is also particularly potent for applications in microfluidics in which the number of resolvable measurements per partition is often severely limited. We prove the identifiability property of the Poisson model under such lax conditions, analytically develop insights into system performance, and confirm these insights in simulated experiments. Our findings encourage a new approach to biosensing and are generalizable to other applications featuring spatial and temporal Poisson signals.

Transfer Learning Can Outperform the True Prior in Double Descent Regularization

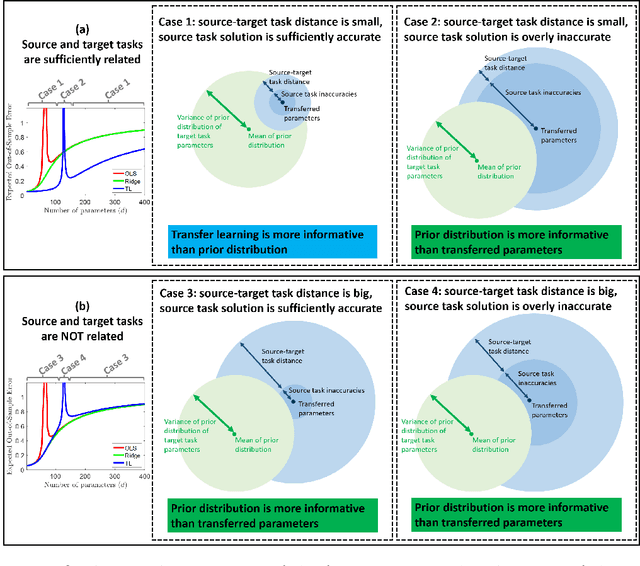
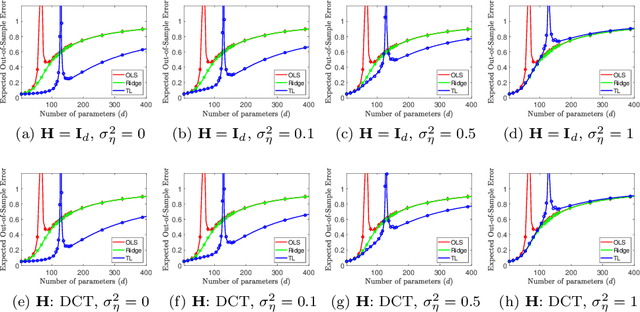
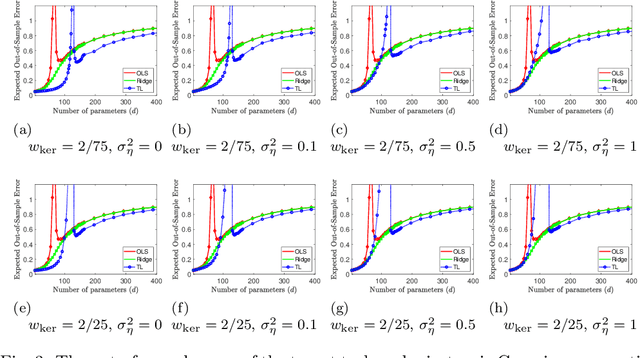
We study a fundamental transfer learning process from source to target linear regression tasks, including overparameterized settings where there are more learned parameters than data samples. The target task learning is addressed by using its training data together with the parameters previously computed for the source task. We define the target task as a linear regression optimization with a regularization on the distance between the to-be-learned target parameters and the already-learned source parameters. This approach can be also interpreted as adjusting the previously learned source parameters for the purpose of the target task, and in the case of sufficiently related tasks this process can be perceived as fine tuning. We analytically characterize the generalization performance of our transfer learning approach and demonstrate its ability to resolve the peak in generalization errors in double descent phenomena of min-norm solutions to ordinary least squares regression. Moreover, we show that for sufficiently related tasks the optimally tuned transfer learning approach can outperform the optimally tuned ridge regression method, even when the true parameter vector conforms with isotropic Gaussian prior distribution. Namely, we demonstrate that transfer learning can beat the minimum mean square error (MMSE) solution of the individual target task.

Wearing a MASK: Compressed Representations of Variable-Length Sequences Using Recurrent Neural Tangent Kernels

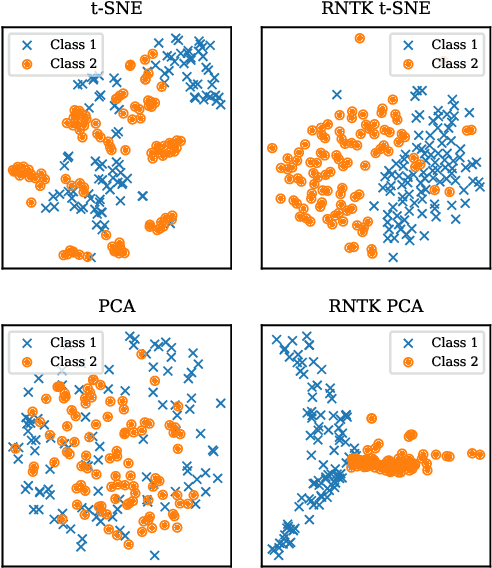
High dimensionality poses many challenges to the use of data, from visualization and interpretation, to prediction and storage for historical preservation. Techniques abound to reduce the dimensionality of fixed-length sequences, yet these methods rarely generalize to variable-length sequences. To address this gap, we extend existing methods that rely on the use of kernels to variable-length sequences via use of the Recurrent Neural Tangent Kernel (RNTK). Since a deep neural network with ReLu activation is a Max-Affine Spline Operator (MASO), we dub our approach Max-Affine Spline Kernel (MASK). We demonstrate how MASK can be used to extend principal components analysis (PCA) and t-distributed stochastic neighbor embedding (t-SNE) and apply these new algorithms to separate synthetic time series data sampled from second-order differential equations.

Diagnostic Questions:The NeurIPS 2020 Education Challenge

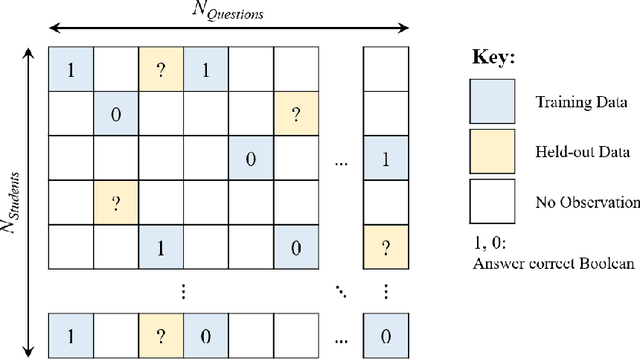
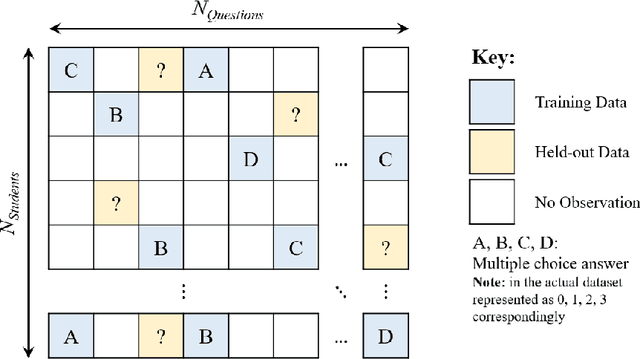
Digital technologies are becoming increasingly prevalent in education, enabling personalized, high quality education resources to be accessible by students across the world. Importantly, among these resources are diagnostic questions: the answers that the students give to these questions reveal key information about the specific nature of misconceptions that the students may hold. Analyzing the massive quantities of data stemming from students' interactions with these diagnostic questions can help us more accurately understand the students' learning status and thus allow us to automate learning curriculum recommendations. In this competition, participants will focus on the students' answer records to these multiple-choice diagnostic questions, with the aim of 1) accurately predicting which answers the students provide; 2) accurately predicting which questions have high quality; and 3) determining a personalized sequence of questions for each student that best predicts the student's answers. These tasks closely mimic the goals of a real-world educational platform and are highly representative of the educational challenges faced today. We provide over 20 million examples of students' answers to mathematics questions from Eedi, a leading educational platform which thousands of students interact with daily around the globe. Participants to this competition have a chance to make a lasting, real-world impact on the quality of personalized education for millions of students across the world.

Ensembles of Generative Adversarial Networks for Disconnected Data

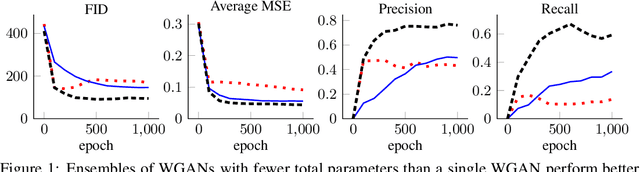
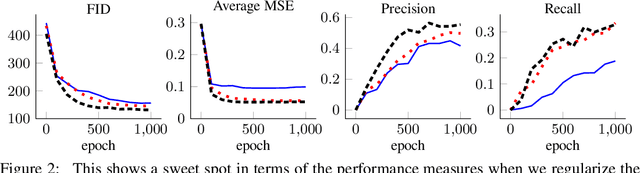
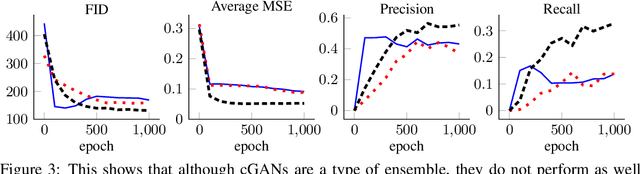
Most current computer vision datasets are composed of disconnected sets, such as images from different classes. We prove that distributions of this type of data cannot be represented with a continuous generative network without error. They can be represented in two ways: With an ensemble of networks or with a single network with truncated latent space. We show that ensembles are more desirable than truncated distributions in practice. We construct a regularized optimization problem that establishes the relationship between a single continuous GAN, an ensemble of GANs, conditional GANs, and Gaussian Mixture GANs. This regularization can be computed efficiently, and we show empirically that our framework has a performance sweet spot which can be found with hyperparameter tuning. This ensemble framework allows better performance than a single continuous GAN or cGAN while maintaining fewer total parameters.

An Improved Semi-Supervised VAE for Learning Disentangled Representations

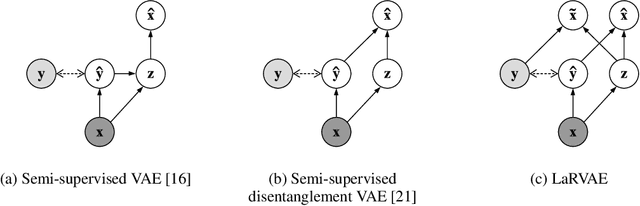
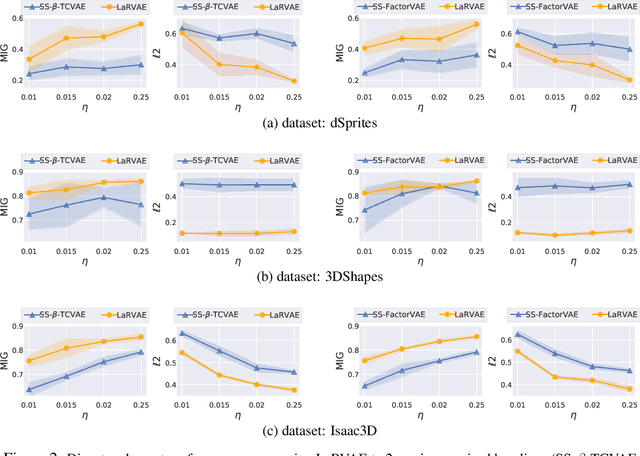
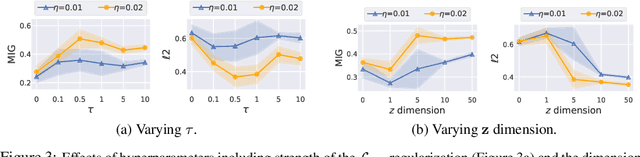
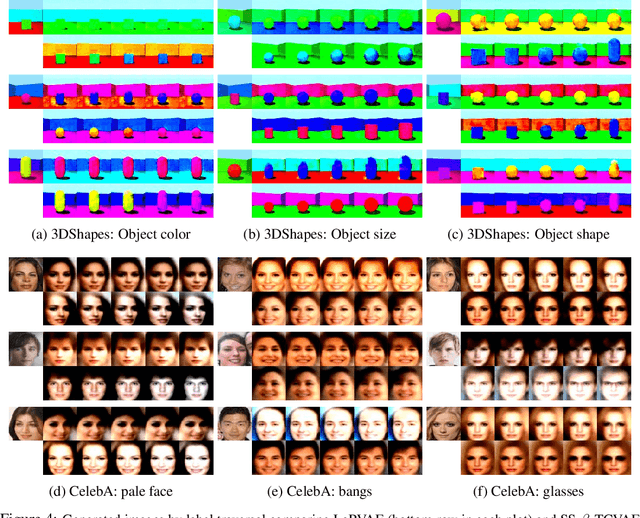
Learning interpretable and disentangled representations is a crucial yet challenging task in representation learning. In this work, we focus on semi-supervised disentanglement learning and extend work by Locatello et al. (2019) by introducing another source of supervision that we denote as label replacement. Specifically, during training, we replace the inferred representation associated with a data point with its ground-truth representation whenever it is available. Our extension is theoretically inspired by our proposed general framework of semi-supervised disentanglement learning in the context of VAEs which naturally motivates the supervised terms commonly used in existing semi-supervised VAEs (but not for disentanglement learning). Extensive experiments on synthetic and real datasets demonstrate both quantitatively and qualitatively the ability of our extension to significantly and consistently improve disentanglement with very limited supervision.

Analytical Probability Distributions and EM-Learning for Deep Generative Networks

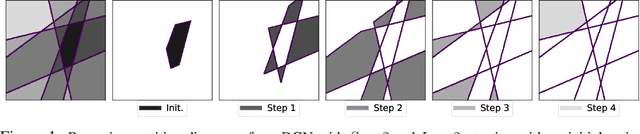
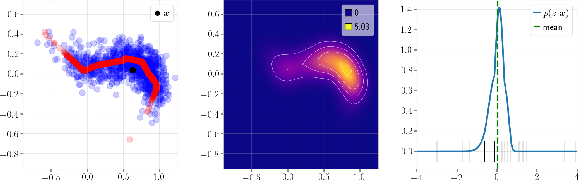
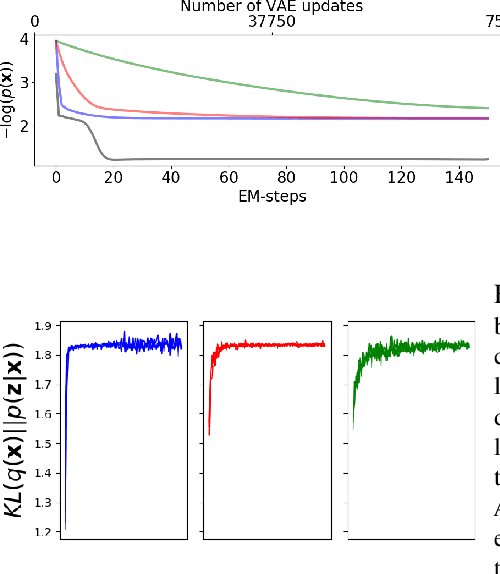
Deep Generative Networks (DGNs) with probabilistic modeling of their output and latent space are currently trained via Variational Autoencoders (VAEs). In the absence of a known analytical form for the posterior and likelihood expectation, VAEs resort to approximations, including (Amortized) Variational Inference (AVI) and Monte-Carlo (MC) sampling. We exploit the Continuous Piecewise Affine (CPA) property of modern DGNs to derive their posterior and marginal distributions as well as the latter's first moments. These findings enable us to derive an analytical Expectation-Maximization (EM) algorithm that enables gradient-free DGN learning. We demonstrate empirically that EM training of DGNs produces greater likelihood than VAE training. Our findings will guide the design of new VAE AVI that better approximate the true posterior and open avenues to apply standard statistical tools for model comparison, anomaly detection, and missing data imputation.

Interpretable Super-Resolution via a Learned Time-Series Representation

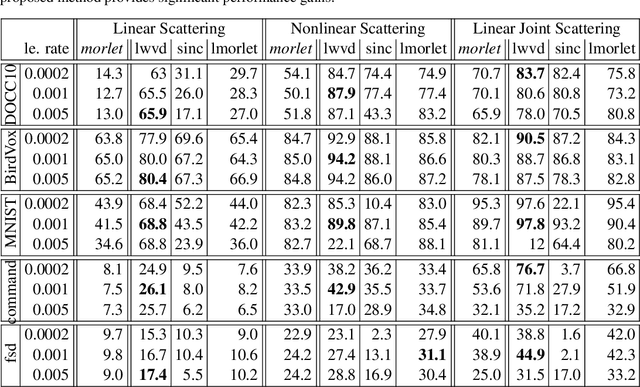
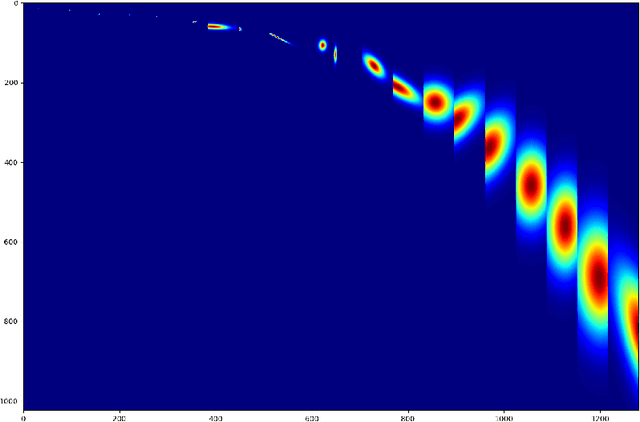
We develop an interpretable and learnable Wigner-Ville distribution that produces a super-resolved quadratic signal representation for time-series analysis. Our approach has two main hallmarks. First, it interpolates between known time-frequency representations (TFRs) in that it can reach super-resolution with increased time and frequency resolution beyond what the Heisenberg uncertainty principle prescribes and thus beyond commonly employed TFRs, Second, it is interpretable thanks to an explicit low-dimensional and physical parameterization of the Wigner-Ville distribution. We demonstrate that our approach is able to learn highly adapted TFRs and is ready and able to tackle various large-scale classification tasks, where we reach state-of-the-art performance compared to baseline and learned TFRs.