Rahul Singh
Multi-Armed Bandits with Dependent Arms
Oct 23, 2020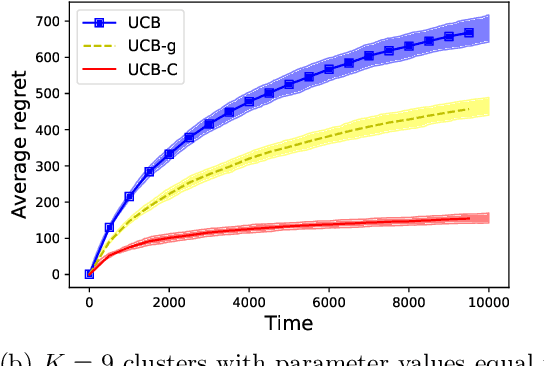
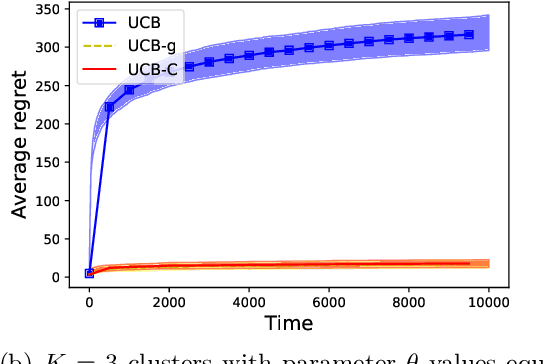
Abstract:We study a variant of the classical multi-armed bandit problem (MABP) which we call as Multi-Armed Bandits with dependent arms. More specifically, multiple arms are grouped together to form a cluster, and the reward distributions of arms belonging to the same cluster are known functions of an unknown parameter that is a characteristic of the cluster. Thus, pulling an arm $i$ not only reveals information about its own reward distribution, but also about all those arms that share the same cluster with arm $i$. This "correlation" amongst the arms complicates the exploration-exploitation trade-off that is encountered in the MABP because the observation dependencies allow us to test simultaneously multiple hypotheses regarding the optimality of an arm. We develop learning algorithms based on the UCB principle which utilize these additional side observations appropriately while performing exploration-exploitation trade-off. We show that the regret of our algorithms grows as $O(K\log T)$, where $K$ is the number of clusters. In contrast, for an algorithm such as the vanilla UCB that is optimal for the classical MABP and does not utilize these dependencies, the regret scales as $O(M\log T)$ where $M$ is the number of arms.
Kernel Methods for Policy Evaluation: Treatment Effects, Mediation Analysis, and Off-Policy Planning
Oct 13, 2020
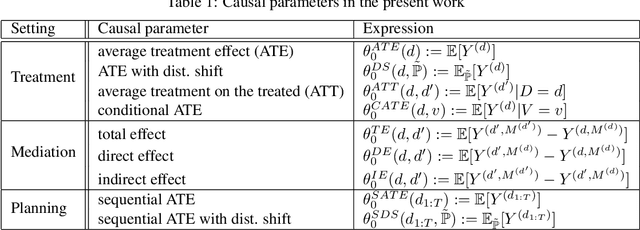
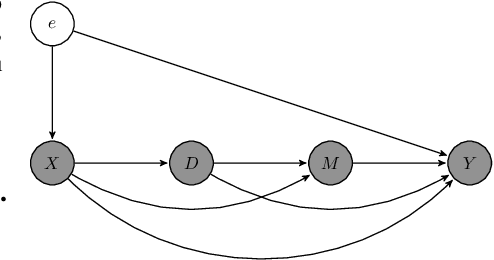
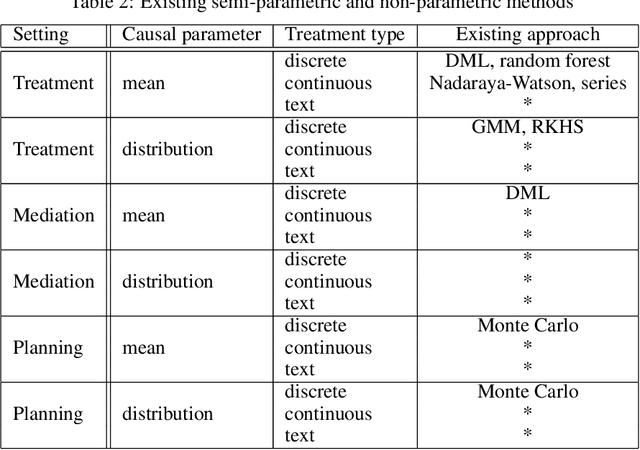
Abstract:We propose a novel framework for non-parametric policy evaluation in static and dynamic settings. Under the assumption of selection on observables, we consider treatment effects of the population, of sub-populations, and of alternative populations that may have alternative covariate distributions. We further consider the decomposition of a total effect into a direct effect and an indirect effect (as mediated by a particular mechanism). Under the assumption of sequential selection on observables, we consider the effects of sequences of treatments. Across settings, we allow for treatments that may be discrete, continuous, or even text. Across settings, we allow for estimation of not only counterfactual mean outcomes but also counterfactual distributions of outcomes. We unify analyses across settings by showing that all of these causal learning problems reduce to the re-weighting of a prediction, i.e. causal adjustment. We implement the re-weighting as an inner product in a function space called a reproducing kernel Hilbert space (RKHS), with a closed form solution that can be computed in one line of code. We prove uniform consistency and provide finite sample rates of convergence. We evaluate our estimators in simulations devised by other authors. We use our new estimators to evaluate continuous and heterogeneous treatment effects of the US Jobs Corps training program for disadvantaged youth.
Model Robustness with Text Classification: Semantic-preserving adversarial attacks
Aug 14, 2020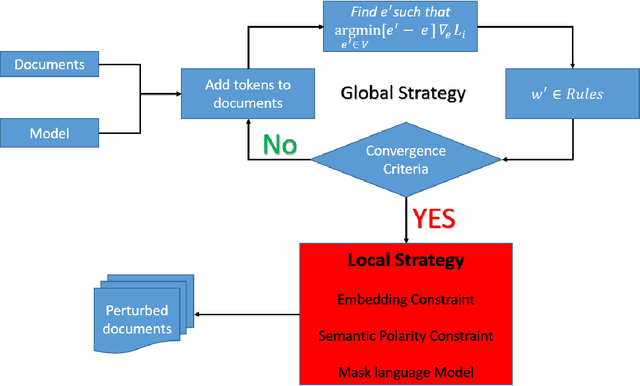



Abstract:We propose algorithms to create adversarial attacks to assess model robustness in text classification problems. They can be used to create white box attacks and black box attacks while at the same time preserving the semantics and syntax of the original text. The attacks cause significant number of flips in white-box setting and same rule based can be used in black-box setting. In a black-box setting, the attacks created are able to reverse decisions of transformer based architectures.
A Partially Observable MDP Approach for Sequential Testing for Infectious Diseases such as COVID-19
Jul 25, 2020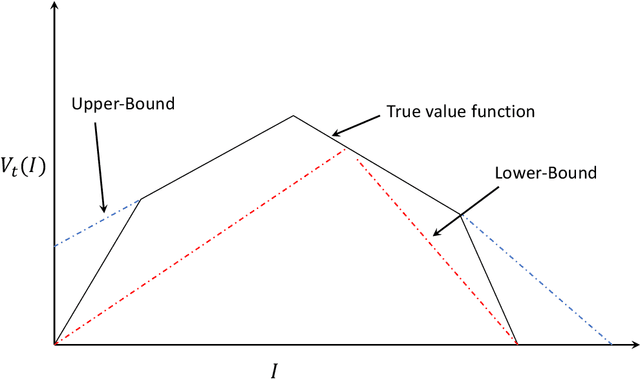
Abstract:The outbreak of the novel coronavirus (COVID-19) is unfolding as a major international crisis whose influence extends to every aspect of our daily lives. Effective testing allows infected individuals to be quarantined, thus reducing the spread of COVID-19, saving countless lives, and helping to restart the economy safely and securely. Developing a good testing strategy can be greatly aided by contact tracing that provides health care providers information about the whereabouts of infected patients in order to determine whom to test. Countries that have been more successful in corralling the virus typically use a ``test, treat, trace, test'' strategy that begins with testing individuals with symptoms, traces contacts of positively tested individuals via a combinations of patient memory, apps, WiFi, GPS, etc., followed by testing their contacts, and repeating this procedure. The problem is that such strategies are myopic and do not efficiently use the testing resources. This is especially the case with COVID-19, where symptoms may show up several days after the infection (or not at all, there is evidence to suggest that many COVID-19 carriers are asymptotic, but may spread the virus). Such greedy strategies, miss out population areas where the virus may be dormant and flare up in the future. In this paper, we show that the testing problem can be cast as a sequential learning-based resource allocation problem with constraints, where the input to the problem is provided by a time-varying social contact graph obtained through various contact tracing tools. We then develop efficient learning strategies that minimize the number of infected individuals. These strategies are based on policy iteration and look-ahead rules. We investigate fundamental performance bounds, and ensure that our solution is robust to errors in the input graph as well as in the tests themselves.
Incremental inference of collective graphical models
Jun 26, 2020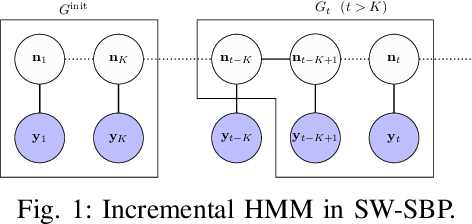
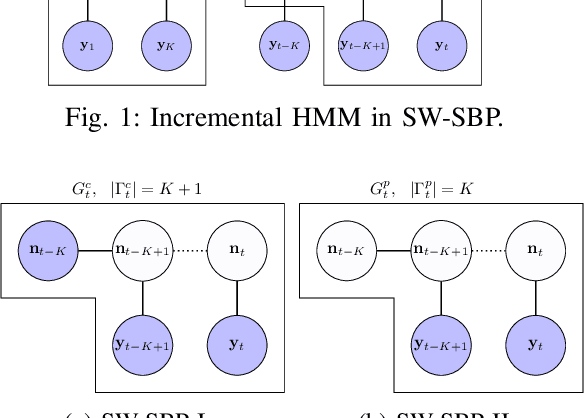
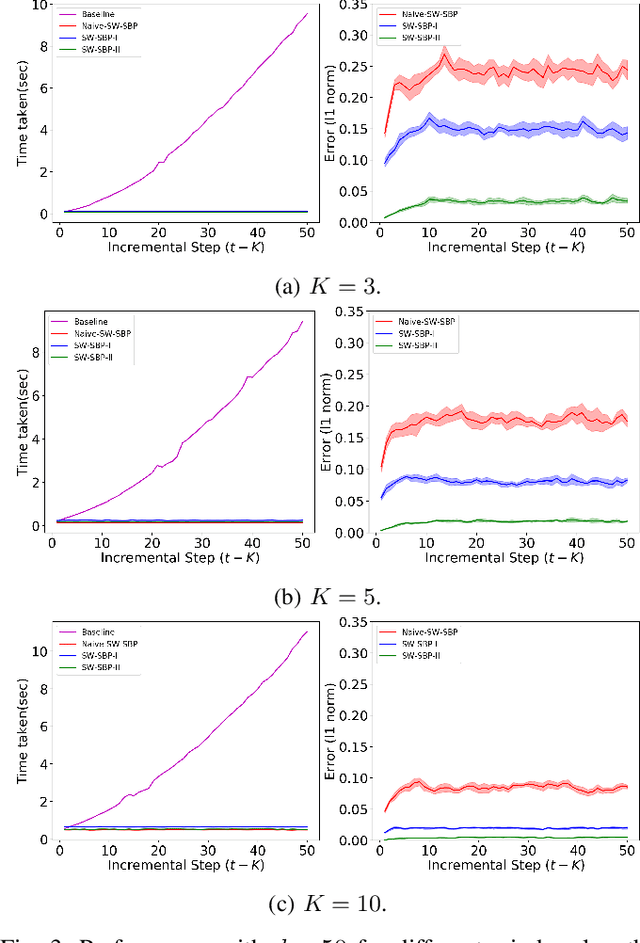
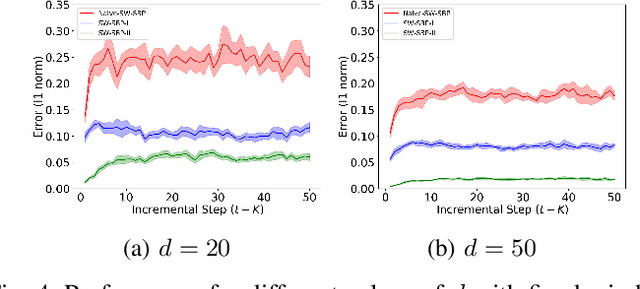
Abstract:We consider incremental inference problems from aggregate data for collective dynamics. In particular, we address the problem of estimating the aggregate marginals of a Markov chain from noisy aggregate observations in an incremental (online) fashion. We propose a sliding window Sinkhorn belief propagation (SW-SBP) algorithm that utilizes a sliding window filter of the most recent noisy aggregate observations along with encoded information from discarded observations. Our algorithm is built upon the recently proposed multi-marginal optimal transport based SBP algorithm that leverages standard belief propagation and Sinkhorn algorithm to solve inference problems from aggregate data. We demonstrate the performance of our algorithm on applications such as inferring population flow from aggregate observations.
Multi-marginal optimal transport and probabilistic graphical models
Jun 25, 2020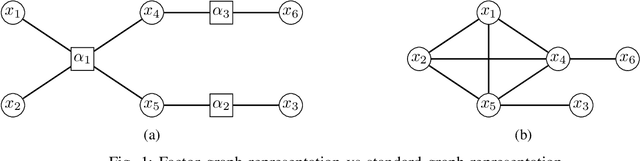

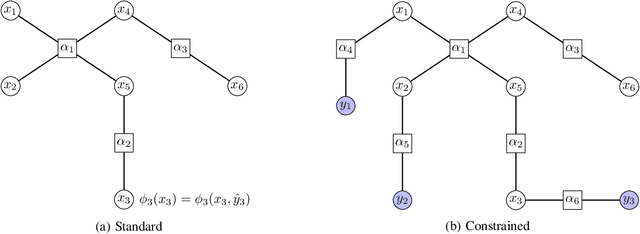
Abstract:We study multi-marginal optimal transport problems from a probabilistic graphical model perspective. We point out an elegant connection between the two when the underlying cost for optimal transport allows a graph structure. In particular, an entropy regularized multi-marginal optimal transport is equivalent to a Bayesian marginal inference problem for probabilistic graphical models with the additional requirement that some of the marginal distributions are specified. This relation on the one hand extends the optimal transport as well as the probabilistic graphical model theories, and on the other hand leads to fast algorithms for multi-marginal optimal transport by leveraging the well-developed algorithms in Bayesian inference. Several numerical examples are provided to highlight the results.
Contextual Bandits with Side-Observations
Jun 06, 2020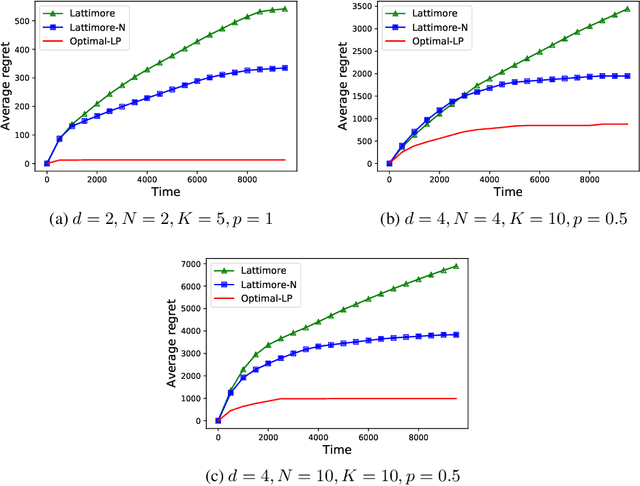
Abstract:We investigate contextual bandits in the presence of side-observations across arms in order to design recommendation algorithms for users connected via social networks. Users in social networks respond to their friends' activity, and hence provide information about each other's preferences. In our model, when a learning algorithm recommends an article to a user, not only does it observe his/her response (e.g. an ad click), but also the side-observations, i.e., the response of his neighbors if they were presented with the same article. We model these observation dependencies by a graph $\mathcal{G}$ in which nodes correspond to users, and edges correspond to social links. We derive a problem/instance-dependent lower-bound on the regret of any consistent algorithm. We propose an optimization (linear programming) based data-driven learning algorithm that utilizes the structure of $\mathcal{G}$ in order to make recommendations to users and show that it is asymptotically optimal, in the sense that its regret matches the lower-bound as the number of rounds $T\to\infty$. We show that this asymptotically optimal regret is upper-bounded as $O\left(|\chi(\mathcal{G})|\log T\right)$, where $|\chi(\mathcal{G})|$ is the domination number of $\mathcal{G}$. In contrast, a naive application of the existing learning algorithms results in $O\left(N\log T\right)$ regret, where $N$ is the number of users.
Improving Robustness via Risk Averse Distributional Reinforcement Learning
May 01, 2020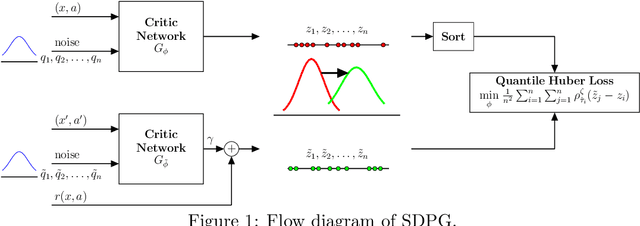
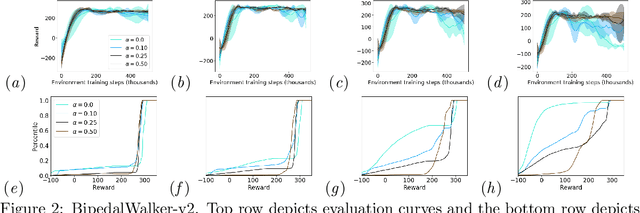
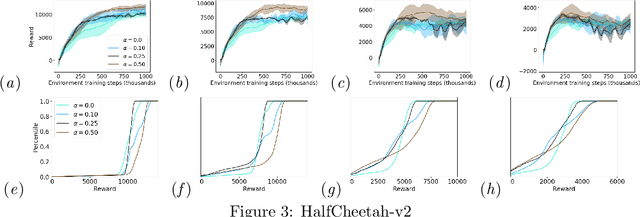
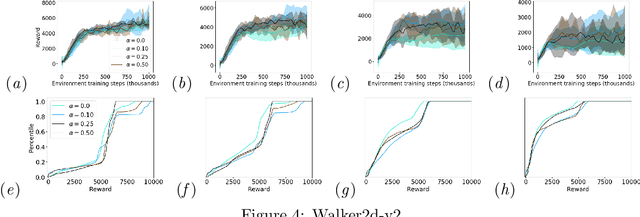
Abstract:One major obstacle that precludes the success of reinforcement learning in real-world applications is the lack of robustness, either to model uncertainties or external disturbances, of the trained policies. Robustness is critical when the policies are trained in simulations instead of real world environment. In this work, we propose a risk-aware algorithm to learn robust policies in order to bridge the gap between simulation training and real-world implementation. Our algorithm is based on recently discovered distributional RL framework. We incorporate CVaR risk measure in sample based distributional policy gradients (SDPG) for learning risk-averse policies to achieve robustness against a range of system disturbances. We validate the robustness of risk-aware SDPG on multiple environments.
Inference with Aggregate Data: An Optimal Transport Approach
Mar 31, 2020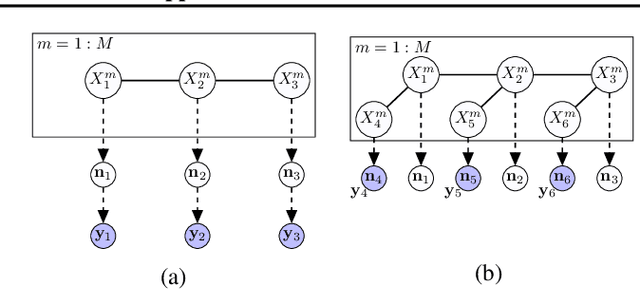
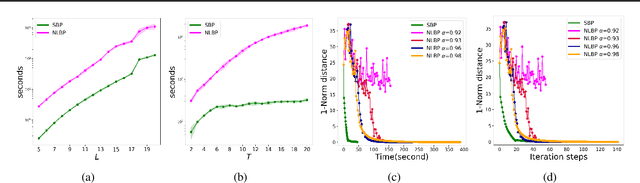
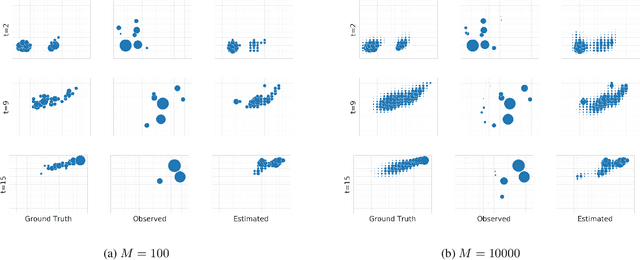
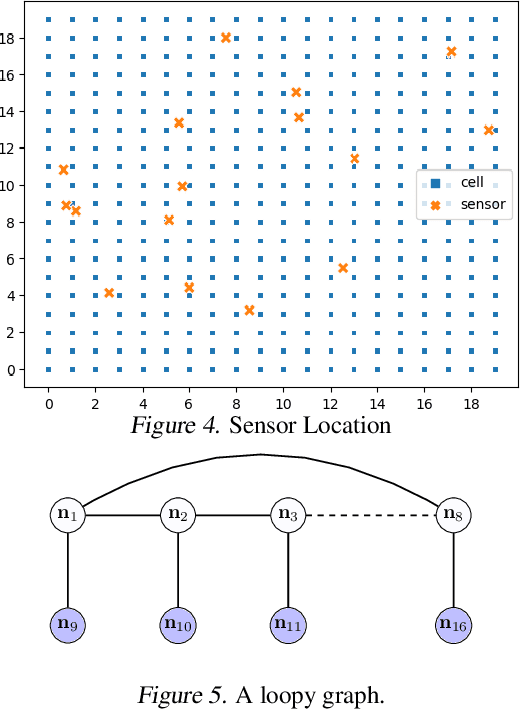
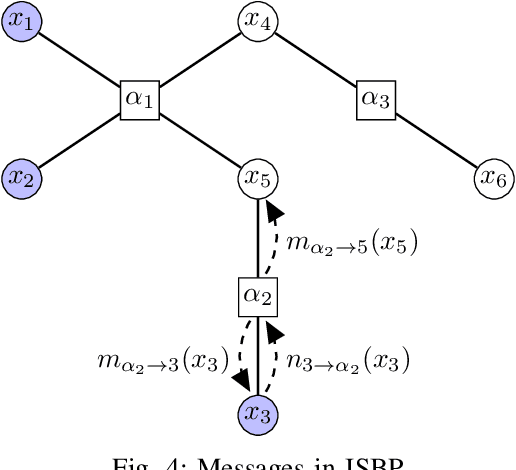
Abstract:We consider inference problems over probabilistic graphical models with aggregate data. In particular, we propose a new efficient belief propagation type algorithm over tree-structured graphs with polynomial computational complexity as well as a global convergence guarantee. This is in contrast to previous methods that either exhibit prohibitive complexity as the population grows or do not guarantee convergence. Our method is based on optimal transport, or more specifically, multi-marginal optimal transport theory. In particular, the inference problem with aggregate observations we consider in this paper can be seen as a structured multi-marginal optimal transport problem, where the cost function decomposes according to the underlying graph. Consequently, the celebrated Sinkhorn algorithm for multi-marginal optimal transport can be leveraged, together with the standard belief propagation algorithm to establish an efficient inference scheme. We demonstrate the performance of our algorithm on applications such as inferring population flow from aggregate observations.
Learning in Networked Control Systems
Mar 21, 2020Abstract:We design adaptive controller (learning rule) for a networked control system (NCS) in which data packets containing control information are transmitted across a lossy wireless channel. We propose Upper Confidence Bounds for Networked Control Systems (UCB-NCS), a learning rule that maintains confidence intervals for the estimates of plant parameters $(A_{(\star)},B_{(\star)})$, and channel reliability $p_{(\star)}$, and utilizes the principle of optimism in the face of uncertainty while making control decisions. We provide non-asymptotic performance guarantees for UCB-NCS by analyzing its "regret", i.e., performance gap from the scenario when $(A_{(\star)},B_{(\star)},p_{(\star)})$ are known to the controller. We show that with a high probability the regret can be upper-bounded as $\tilde{O}\left(C\sqrt{T}\right)$\footnote{Here $\tilde{O}$ hides logarithmic factors.}, where $T$ is the operating time horizon of the system, and $C$ is a problem dependent constant.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge