From Large to Small Datasets: Size Generalization for Clustering Algorithm Selection

In clustering algorithm selection, we are given a massive dataset and must efficiently select which clustering algorithm to use. We study this problem in a semi-supervised setting, with an unknown ground-truth clustering that we can only access through expensive oracle queries. Ideally, the clustering algorithm's output will be structurally close to the ground truth. We approach this problem by introducing a notion of size generalization for clustering algorithm accuracy. We identify conditions under which we can (1) subsample the massive clustering instance, (2) evaluate a set of candidate algorithms on the smaller instance, and (3) guarantee that the algorithm with the best accuracy on the small instance will have the best accuracy on the original big instance. We provide theoretical size generalization guarantees for three classic clustering algorithms: single-linkage, k-means++, and (a smoothed variant of) Gonzalez's k-centers heuristic. We validate our theoretical analysis with empirical results, observing that on real-world clustering instances, we can use a subsample of as little as 5% of the data to identify which algorithm is best on the full dataset.

On Scrambling Phenomena for Randomly Initialized Recurrent Networks

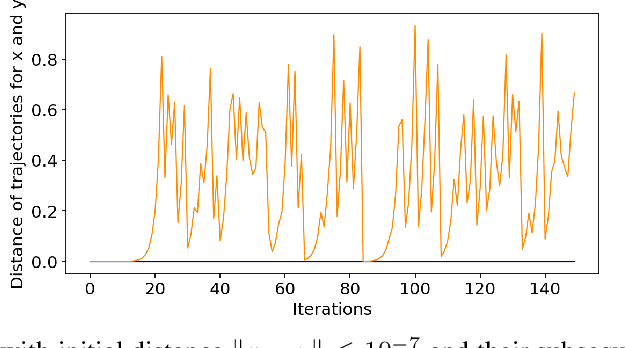
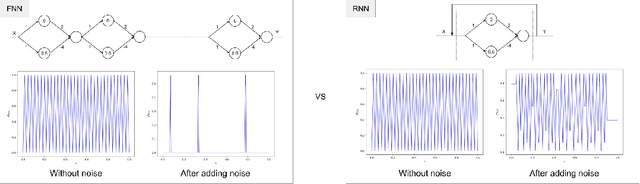
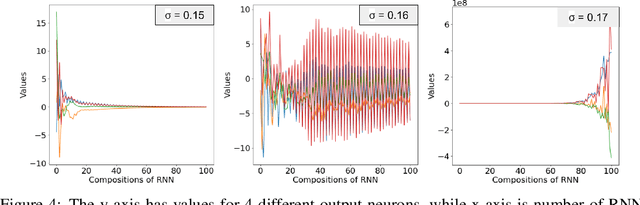
Recurrent Neural Networks (RNNs) frequently exhibit complicated dynamics, and their sensitivity to the initialization process often renders them notoriously hard to train. Recent works have shed light on such phenomena analyzing when exploding or vanishing gradients may occur, either of which is detrimental for training dynamics. In this paper, we point to a formal connection between RNNs and chaotic dynamical systems and prove a qualitatively stronger phenomenon about RNNs than what exploding gradients seem to suggest. Our main result proves that under standard initialization (e.g., He, Xavier etc.), RNNs will exhibit \textit{Li-Yorke chaos} with \textit{constant} probability \textit{independent} of the network's width. This explains the experimentally observed phenomenon of \textit{scrambling}, under which trajectories of nearby points may appear to be arbitrarily close during some timesteps, yet will be far away in future timesteps. In stark contrast to their feedforward counterparts, we show that chaotic behavior in RNNs is preserved under small perturbations and that their expressive power remains exponential in the number of feedback iterations. Our technical arguments rely on viewing RNNs as random walks under non-linear activations, and studying the existence of certain types of higher-order fixed points called \textit{periodic points} that lead to phase transitions from order to chaos.

Efficiently Computing Nash Equilibria in Adversarial Team Markov Games

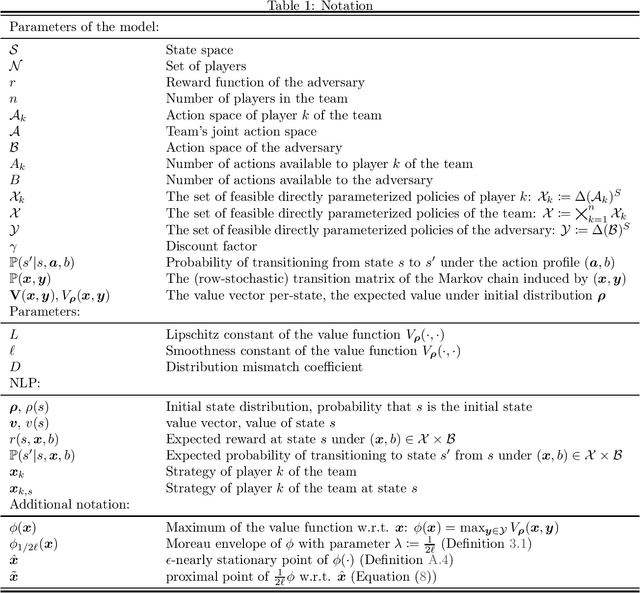
Computing Nash equilibrium policies is a central problem in multi-agent reinforcement learning that has received extensive attention both in theory and in practice. However, provable guarantees have been thus far either limited to fully competitive or cooperative scenarios or impose strong assumptions that are difficult to meet in most practical applications. In this work, we depart from those prior results by investigating infinite-horizon \emph{adversarial team Markov games}, a natural and well-motivated class of games in which a team of identically-interested players -- in the absence of any explicit coordination or communication -- is competing against an adversarial player. This setting allows for a unifying treatment of zero-sum Markov games and Markov potential games, and serves as a step to model more realistic strategic interactions that feature both competing and cooperative interests. Our main contribution is the first algorithm for computing stationary $\epsilon$-approximate Nash equilibria in adversarial team Markov games with computational complexity that is polynomial in all the natural parameters of the game, as well as $1/\epsilon$. The proposed algorithm is particularly natural and practical, and it is based on performing independent policy gradient steps for each player in the team, in tandem with best responses from the side of the adversary; in turn, the policy for the adversary is then obtained by solving a carefully constructed linear program. Our analysis leverages non-standard techniques to establish the KKT optimality conditions for a nonlinear program with nonconvex constraints, thereby leading to a natural interpretation of the induced Lagrange multipliers. Along the way, we significantly extend an important characterization of optimal policies in adversarial (normal-form) team games due to Von Stengel and Koller (GEB `97).

Expressivity of Neural Networks via Chaotic Itineraries beyond Sharkovsky's Theorem

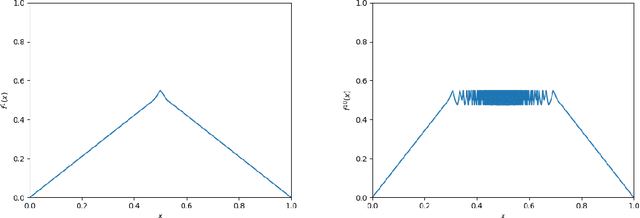
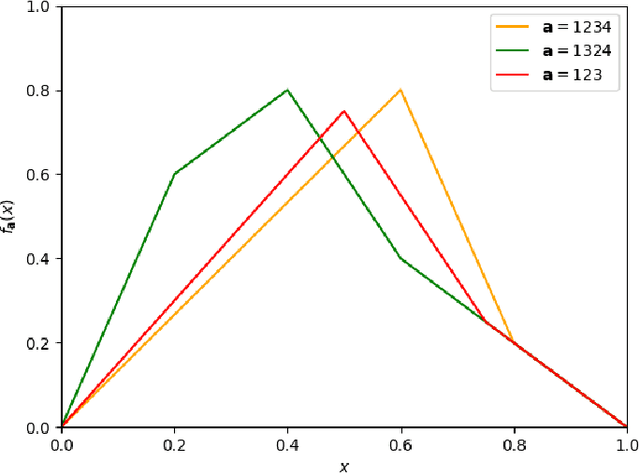
Given a target function $f$, how large must a neural network be in order to approximate $f$? Recent works examine this basic question on neural network \textit{expressivity} from the lens of dynamical systems and provide novel ``depth-vs-width'' tradeoffs for a large family of functions $f$. They suggest that such tradeoffs are governed by the existence of \textit{periodic} points or \emph{cycles} in $f$. Our work, by further deploying dynamical systems concepts, illuminates a more subtle connection between periodicity and expressivity: we prove that periodic points alone lead to suboptimal depth-width tradeoffs and we improve upon them by demonstrating that certain ``chaotic itineraries'' give stronger exponential tradeoffs, even in regimes where previous analyses only imply polynomial gaps. Contrary to prior works, our bounds are nearly-optimal, tighten as the period increases, and handle strong notions of inapproximability (e.g., constant $L_1$ error). More broadly, we identify a phase transition to the \textit{chaotic regime} that exactly coincides with an abrupt shift in other notions of function complexity, including VC-dimension and topological entropy.

From Trees to Continuous Embeddings and Back: Hyperbolic Hierarchical Clustering

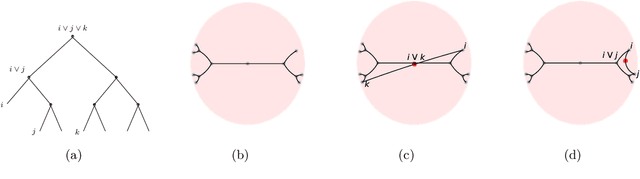
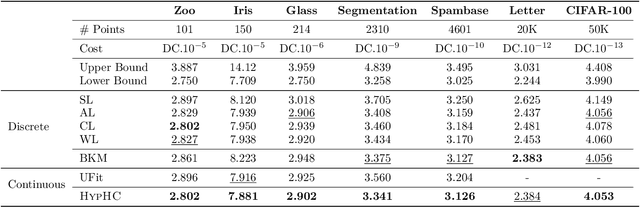
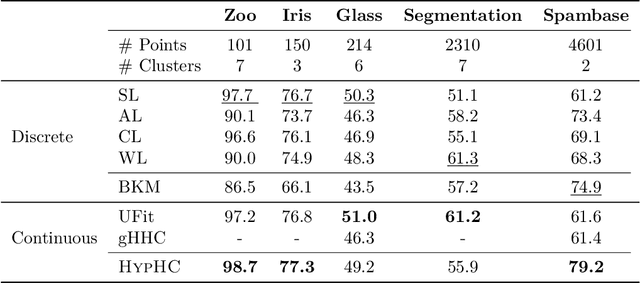
Similarity-based Hierarchical Clustering (HC) is a classical unsupervised machine learning algorithm that has traditionally been solved with heuristic algorithms like Average-Linkage. Recently, Dasgupta reframed HC as a discrete optimization problem by introducing a global cost function measuring the quality of a given tree. In this work, we provide the first continuous relaxation of Dasgupta's discrete optimization problem with provable quality guarantees. The key idea of our method, HypHC, is showing a direct correspondence from discrete trees to continuous representations (via the hyperbolic embeddings of their leaf nodes) and back (via a decoding algorithm that maps leaf embeddings to a dendrogram), allowing us to search the space of discrete binary trees with continuous optimization. Building on analogies between trees and hyperbolic space, we derive a continuous analogue for the notion of lowest common ancestor, which leads to a continuous relaxation of Dasgupta's discrete objective. We can show that after decoding, the global minimizer of our continuous relaxation yields a discrete tree with a (1 + epsilon)-factor approximation for Dasgupta's optimal tree, where epsilon can be made arbitrarily small and controls optimization challenges. We experimentally evaluate HypHC on a variety of HC benchmarks and find that even approximate solutions found with gradient descent have superior clustering quality than agglomerative heuristics or other gradient based algorithms. Finally, we highlight the flexibility of HypHC using end-to-end training in a downstream classification task.

Better Depth-Width Trade-offs for Neural Networks through the lens of Dynamical Systems

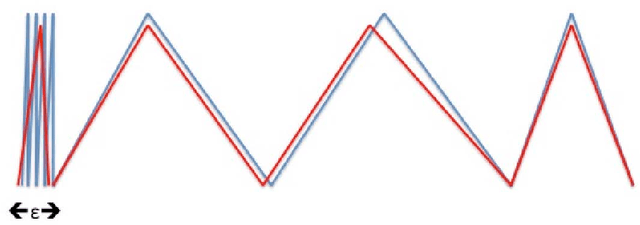
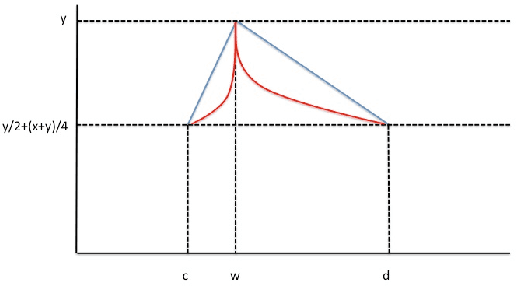
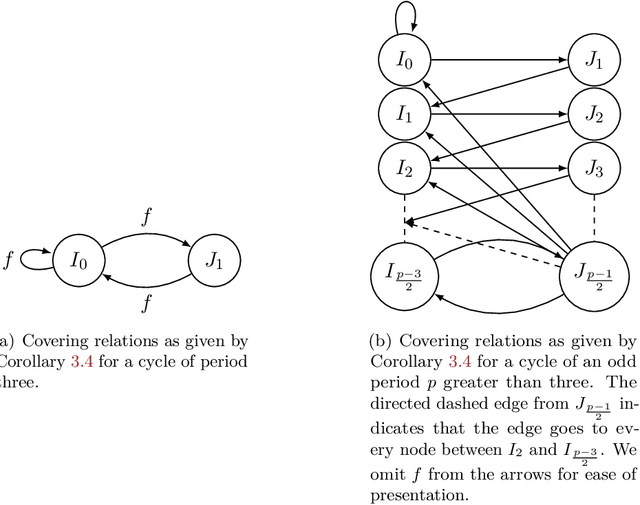
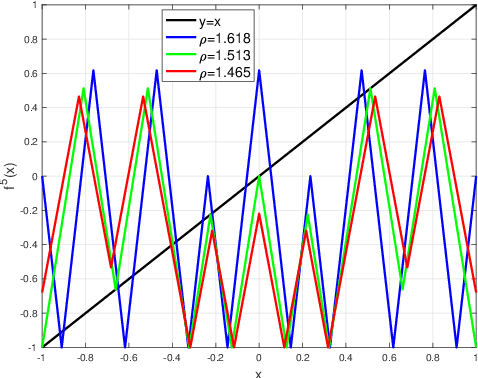
The expressivity of neural networks as a function of their depth, width and type of activation units has been an important question in deep learning theory. Recently, depth separation results for ReLU networks were obtained via a new connection with dynamical systems, using a generalized notion of fixed points of a continuous map $f$, called periodic points. In this work, we strengthen the connection with dynamical systems and we improve the existing width lower bounds along several aspects. Our first main result is period-specific width lower bounds that hold under the stronger notion of $L^1$-approximation error, instead of the weaker classification error. Our second contribution is that we provide sharper width lower bounds, still yielding meaningful exponential depth-width separations, in regimes where previous results wouldn't apply. A byproduct of our results is that there exists a universal constant characterizing the depth-width trade-offs, as long as $f$ has odd periods. Technically, our results follow by unveiling a tighter connection between the following three quantities of a given function: its period, its Lipschitz constant and the growth rate of the number of oscillations arising under compositions of the function $f$ with itself.

Depth-Width Trade-offs for ReLU Networks via Sharkovsky's Theorem

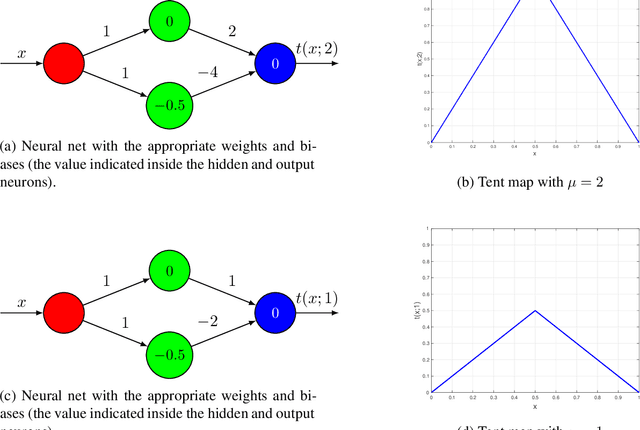
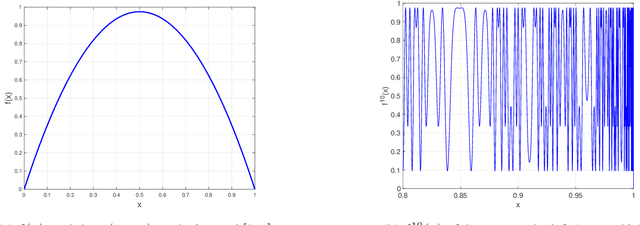
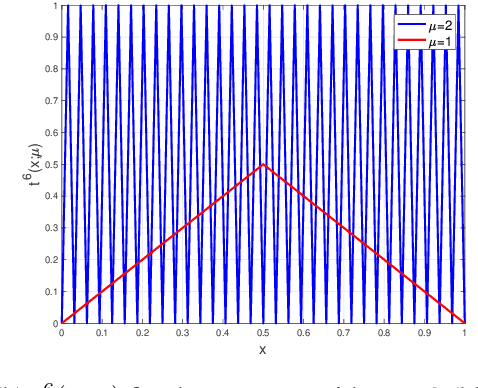
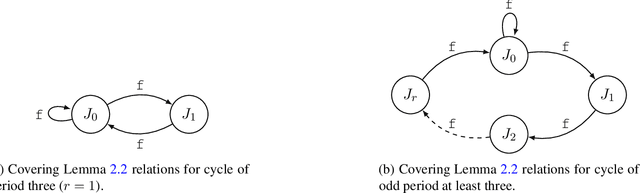
Understanding the representational power of Deep Neural Networks (DNNs) and how their structural properties (e.g., depth, width, type of activation unit) affect the functions they can compute, has been an important yet challenging question in deep learning and approximation theory. In a seminal paper, Telgarsky highlighted the benefits of depth by presenting a family of functions (based on simple triangular waves) for which DNNs achieve zero classification error, whereas shallow networks with fewer than exponentially many nodes incur constant error. Even though Telgarsky's work reveals the limitations of shallow neural networks, it does not inform us on why these functions are difficult to represent and in fact he states it as a tantalizing open question to characterize those functions that cannot be well-approximated by smaller depths. In this work, we point to a new connection between DNNs expressivity and Sharkovsky's Theorem from dynamical systems, that enables us to characterize the depth-width trade-offs of ReLU networks for representing functions based on the presence of generalized notion of fixed points, called periodic points (a fixed point is a point of period 1). Motivated by our observation that the triangle waves used in Telgarsky's work contain points of period 3 - a period that is special in that it implies chaotic behavior based on the celebrated result by Li-Yorke - we proceed to give general lower bounds for the width needed to represent periodic functions as a function of the depth. Technically, the crux of our approach is based on an eigenvalue analysis of the dynamical system associated with such functions.

Adversarially Robust Low Dimensional Representations

Adversarial or test time robustness measures the susceptibility of a machine learning system to small perturbations made to the input at test time. This has attracted much interest on the empirical side, since many existing ML systems perform poorly under imperceptible adversarial perturbations to the test inputs. On the other hand, our theoretical understanding of this phenomenon is limited, and has mostly focused on supervised learning tasks. In this work we study the problem of computing adversarially robust representations of data. We formulate a natural extension of Principal Component Analysis (PCA) where the goal is to find a low dimensional subspace to represent the given data with minimum projection error, and that is in addition robust to small perturbations measured in $\ell_q$ norm (say $q=\infty$). Unlike PCA which is solvable in polynomial time, our formulation is computationally intractable to optimize as it captures the well-studied sparse PCA objective. We show the following algorithmic and statistical results. - Polynomial time algorithms in the worst-case that achieve constant factor approximations to the objective while only violating the robustness constraint by a constant factor. - We prove that our formulation (and algorithms) also enjoy significant statistical benefits in terms of sample complexity over standard PCA on account of a "regularization effect", that is formalized using the well-studied spiked covariance model. - Surprisingly, we show that our algorithmic techniques can also be made robust to corruptions in the training data, in addition to yielding representations that are robust at test time! Here an adversary is allowed to corrupt potentially every data point up to a specified amount in the $\ell_q$ norm. We further apply these techniques for mean estimation and clustering under adversarial corruptions to the training data.

Hierarchical Clustering better than Average-Linkage

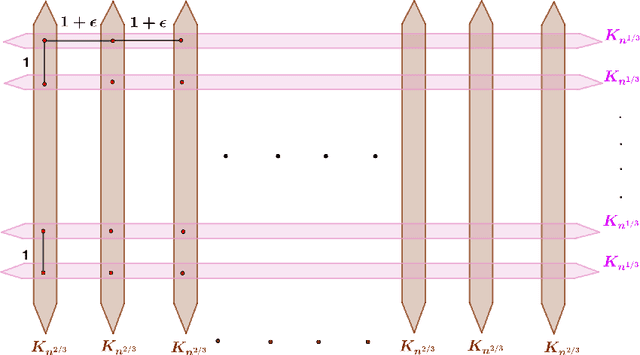
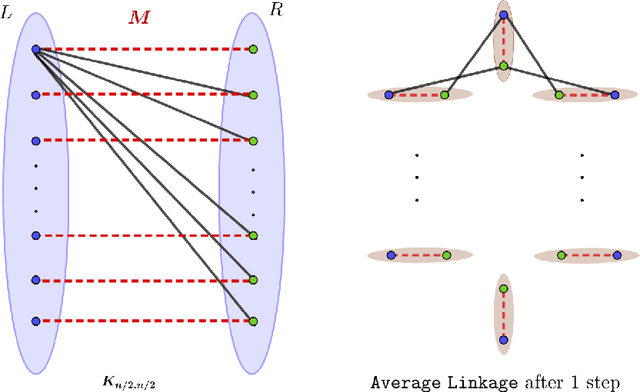
Hierarchical Clustering (HC) is a widely studied problem in exploratory data analysis, usually tackled by simple agglomerative procedures like average-linkage, single-linkage or complete-linkage. In this paper we focus on two objectives, introduced recently to give insight into the performance of average-linkage clustering: a similarity based HC objective proposed by [Moseley and Wang, 2017] and a dissimilarity based HC objective proposed by [Cohen-Addad et al., 2018]. In both cases, we present tight counterexamples showing that average-linkage cannot obtain better than 1/3 and 2/3 approximations respectively (in the worst-case), settling an open question raised in [Moseley and Wang, 2017]. This matches the approximation ratio of a random solution, raising a natural question: can we beat average-linkage for these objectives? We answer this in the affirmative, giving two new algorithms based on semidefinite programming with provably better guarantees.

Hierarchical Clustering with Structural Constraints

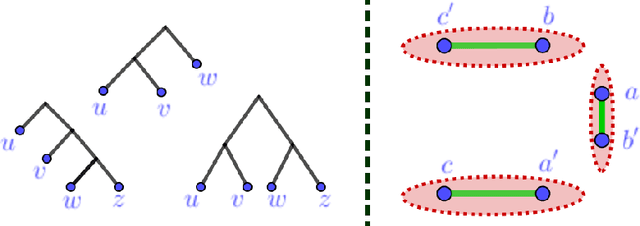
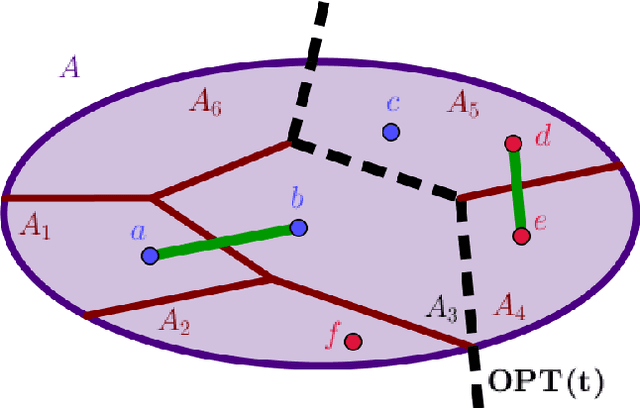
Hierarchical clustering is a popular unsupervised data analysis method. For many real-world applications, we would like to exploit prior information about the data that imposes constraints on the clustering hierarchy, and is not captured by the set of features available to the algorithm. This gives rise to the problem of "hierarchical clustering with structural constraints". Structural constraints pose major challenges for bottom-up approaches like average/single linkage and even though they can be naturally incorporated into top-down divisive algorithms, no formal guarantees exist on the quality of their output. In this paper, we provide provable approximation guarantees for two simple top-down algorithms, using a recently introduced optimization viewpoint of hierarchical clustering with pairwise similarity information [Dasgupta, 2016]. We show how to find good solutions even in the presence of conflicting prior information, by formulating a constraint-based regularization of the objective. We further explore a variation of this objective for dissimilarity information [Cohen-Addad et al., 2018] and improve upon current techniques. Finally, we demonstrate our approach on a real dataset for the taxonomy application.