Pipeline Gradient-based Model Training on Analog In-memory Accelerators

Aiming to accelerate the training of large deep neural models (DNN) in an energy-efficient way, an analog in-memory computing (AIMC) accelerator emerges as a solution with immense potential. In AIMC accelerators, trainable weights are kept in memory without the need to move from memory to processors during the training, reducing a bunch of overhead. However, although the in-memory feature enables efficient computation, it also constrains the use of data parallelism since copying weights from one AIMC to another is expensive. To enable parallel training using AIMC, we propose synchronous and asynchronous pipeline parallelism for AIMC accelerators inspired by the pipeline in digital domains. This paper provides a theoretical convergence guarantee for both synchronous and asynchronous pipelines in terms of both sampling and clock cycle complexity, which is non-trivial since the physical characteristic of AIMC accelerators leads to analog updates that suffer from asymmetric bias. The simulations of training DNN on real datasets verify the efficiency of pipeline training.

Unlocking Global Optimality in Bilevel Optimization: A Pilot Study

Bilevel optimization has witnessed a resurgence of interest, driven by its critical role in trustworthy and efficient machine learning applications. Recent research has focused on proposing efficient methods with provable convergence guarantees. However, while many prior works have established convergence to stationary points or local minima, obtaining the global optimum of bilevel optimization remains an important yet open problem. The difficulty lies in the fact that unlike many prior non-convex single-level problems, this bilevel problem does not admit a ``benign" landscape, and may indeed have multiple spurious local solutions. Nevertheless, attaining the global optimality is indispensable for ensuring reliability, safety, and cost-effectiveness, particularly in high-stakes engineering applications that rely on bilevel optimization. In this paper, we first explore the challenges of establishing a global convergence theory for bilevel optimization, and present two sufficient conditions for global convergence. We provide algorithm-specific proofs to rigorously substantiate these sufficient conditions along the optimization trajectory, focusing on two specific bilevel learning scenarios: representation learning and data hypercleaning (a.k.a. reweighting). Experiments corroborate the theoretical findings, demonstrating convergence to global minimum in both cases.

A Primal-Dual-Assisted Penalty Approach to Bilevel Optimization with Coupled Constraints

Interest in bilevel optimization has grown in recent years, partially due to its applications to tackle challenging machine-learning problems. Several exciting recent works have been centered around developing efficient gradient-based algorithms that can solve bilevel optimization problems with provable guarantees. However, the existing literature mainly focuses on bilevel problems either without constraints, or featuring only simple constraints that do not couple variables across the upper and lower levels, excluding a range of complex applications. Our paper studies this challenging but less explored scenario and develops a (fully) first-order algorithm, which we term BLOCC, to tackle BiLevel Optimization problems with Coupled Constraints. We establish rigorous convergence theory for the proposed algorithm and demonstrate its effectiveness on two well-known real-world applications - hyperparameter selection in support vector machine (SVM) and infrastructure planning in transportation networks using the real data from the city of Seville.

A Generalized Alternating Method for Bilevel Learning under the Polyak-Łojasiewicz Condition

Bilevel optimization has recently regained interest owing to its applications in emerging machine learning fields such as hyperparameter optimization, meta-learning, and reinforcement learning. Recent results have shown that simple alternating (implicit) gradient-based algorithms can achieve the same convergence rate of single-level gradient descent (GD) for bilevel problems with a strongly convex lower-level objective. However, it remains unclear whether this result can be generalized to bilevel problems beyond this basic setting. In this paper, we propose a Generalized ALternating mEthod for bilevel opTimization (GALET) with a nonconvex lower-level objective that satisfies the Polyak-{\L}ojasiewicz (PL) condition. We first introduce a stationary metric for the considered bilevel problems, which generalizes the existing metric. We then establish that GALET achieves an $\epsilon$-stationary metric for the considered problem within $\tilde{\cal O}(\epsilon^{-1})$ iterations, which matches the iteration complexity of GD for smooth nonconvex problems.

Alternating Implicit Projected SGD and Its Efficient Variants for Equality-constrained Bilevel Optimization

Stochastic bilevel optimization, which captures the inherent nested structure of machine learning problems, is gaining popularity in many recent applications. Existing works on bilevel optimization mostly consider either unconstrained problems or constrained upper-level problems. This paper considers the stochastic bilevel optimization problems with equality constraints both in the upper and lower levels. By leveraging the special structure of the equality constraints problem, the paper first presents an alternating implicit projected SGD approach and establishes the $\tilde{\cal O}(\epsilon^{-2})$ sample complexity that matches the state-of-the-art complexity of ALSET \citep{chen2021closing} for unconstrained bilevel problems. To further save the cost of projection, the paper presents two alternating implicit projection-efficient SGD approaches, where one algorithm enjoys the $\tilde{\cal O}(\epsilon^{-2}/T)$ upper-level and ${\cal O}(\epsilon^{-1.5}/T^{\frac{3}{4}})$ lower-level projection complexity with ${\cal O}(T)$ lower-level batch size, and the other one enjoys $\tilde{\cal O}(\epsilon^{-1.5})$ upper-level and lower-level projection complexity with ${\cal O}(1)$ batch size. Application to federated bilevel optimization has been presented to showcase the empirical performance of our algorithms. Our results demonstrate that equality-constrained bilevel optimization with strongly-convex lower-level problems can be solved as efficiently as stochastic single-level optimization problems.

Lazy Queries Can Reduce Variance in Zeroth-order Optimization

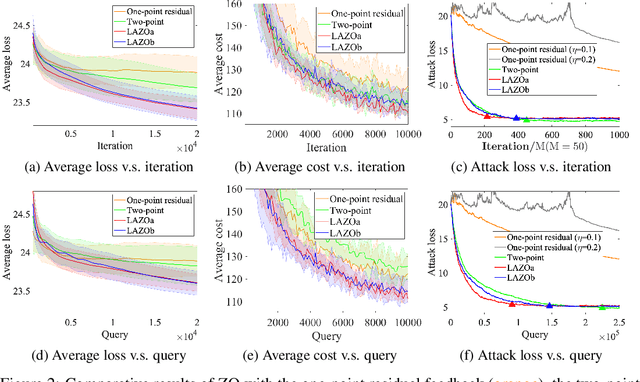
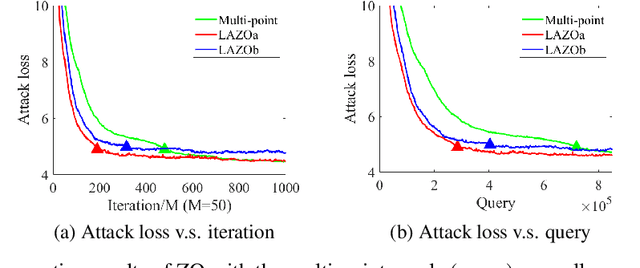
A major challenge of applying zeroth-order (ZO) methods is the high query complexity, especially when queries are costly. We propose a novel gradient estimation technique for ZO methods based on adaptive lazy queries that we term as LAZO. Different from the classic one-point or two-point gradient estimation methods, LAZO develops two alternative ways to check the usefulness of old queries from previous iterations, and then adaptively reuses them to construct the low-variance gradient estimates. We rigorously establish that through judiciously reusing the old queries, LAZO can reduce the variance of stochastic gradient estimates so that it not only saves queries per iteration but also achieves the regret bound for the symmetric two-point method. We evaluate the numerical performance of LAZO, and demonstrate the low-variance property and the performance gain of LAZO in both regret and query complexity relative to several existing ZO methods. The idea of LAZO is general, and can be applied to other variants of ZO methods.

Sharp-MAML: Sharpness-Aware Model-Agnostic Meta Learning

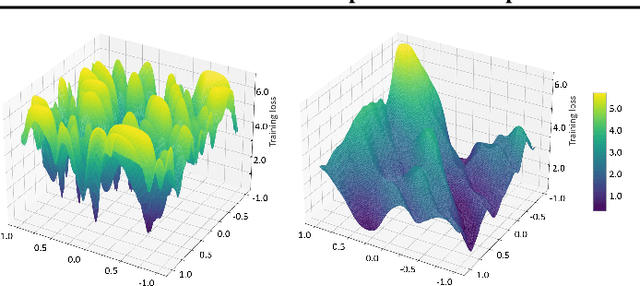
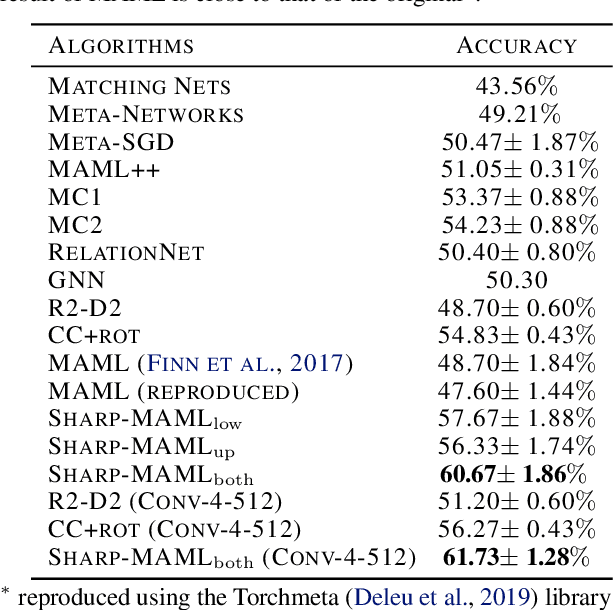
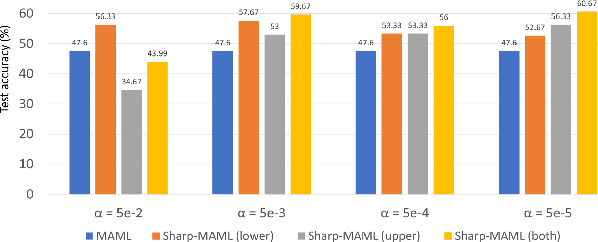
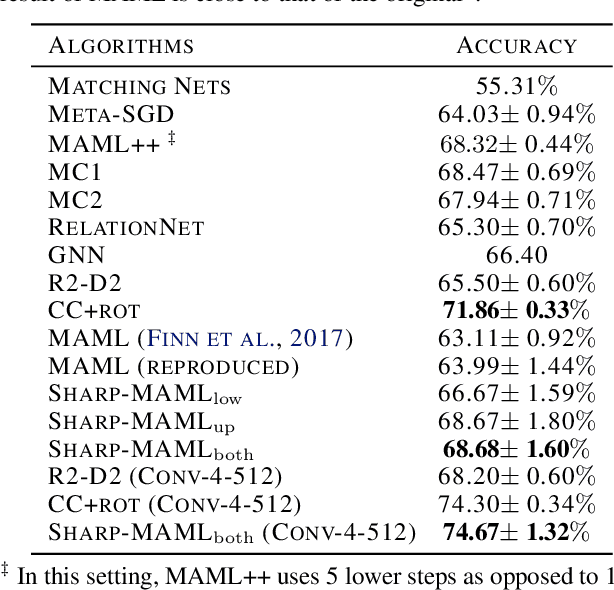
Model-agnostic meta learning (MAML) is currently one of the dominating approaches for few-shot meta-learning. Albeit its effectiveness, the optimization of MAML can be challenging due to the innate bilevel problem structure. Specifically, the loss landscape of MAML is much more complex with possibly more saddle points and local minimizers than its empirical risk minimization counterpart. To address this challenge, we leverage the recently invented sharpness-aware minimization and develop a sharpness-aware MAML approach that we term Sharp-MAML. We empirically demonstrate that Sharp-MAML and its computation-efficient variant can outperform popular existing MAML baselines (e.g., $+12\%$ accuracy on Mini-Imagenet). We complement the empirical study with the convergence rate analysis and the generalization bound of Sharp-MAML. To the best of our knowledge, this is the first empirical and theoretical study on sharpness-aware minimization in the context of bilevel learning. The code is available at https://github.com/mominabbass/Sharp-MAML.

Image denoising via K-SVD with primal-dual active set algorithm

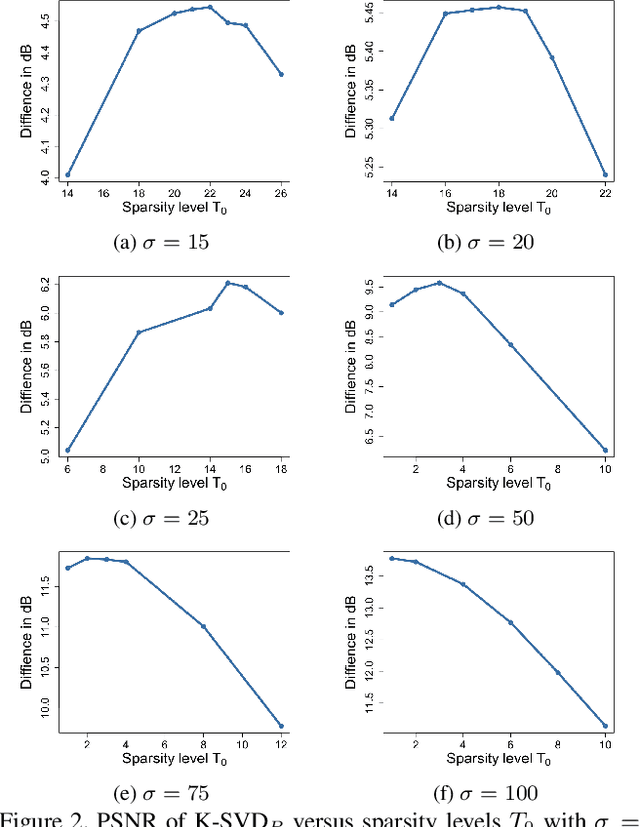
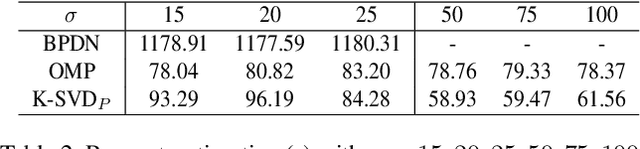
K-SVD algorithm has been successfully applied to image denoising tasks dozens of years but the big bottleneck in speed and accuracy still needs attention to break. For the sparse coding stage in K-SVD, which involves $\ell_{0}$ constraint, prevailing methods usually seek approximate solutions greedily but are less effective once the noise level is high. The alternative $\ell_{1}$ optimization is proved to be powerful than $\ell_{0}$, however, the time consumption prevents it from the implementation. In this paper, we propose a new K-SVD framework called K-SVD$_P$ by applying the Primal-dual active set (PDAS) algorithm to it. Different from the greedy algorithms based K-SVD, the K-SVD$_P$ algorithm develops a selection strategy motivated by KKT (Karush-Kuhn-Tucker) condition and yields to an efficient update in the sparse coding stage. Since the K-SVD$_P$ algorithm seeks for an equivalent solution to the dual problem iteratively with simple explicit expression in this denoising problem, speed and quality of denoising can be reached simultaneously. Experiments are carried out and demonstrate the comparable denoising performance of our K-SVD$_P$ with state-of-the-art methods.