From Atoms to Chains: Divergence-Guided Reasoning Curriculum for Unlabeled LLM Domain Adaptation

Adapting Large Language Models (LLMs) to specialized domains without human-annotated data is a crucial yet formidable challenge. Widely adopted knowledge distillation methods often devolve into coarse-grained mimicry, where the student model inefficiently targets its own weaknesses and risks inheriting the teacher's reasoning flaws. This exposes a critical pedagogical dilemma: how to devise a reliable curriculum when the teacher itself is not an infallible expert. Our work resolves this by capitalizing on a key insight: while LLMs may exhibit fallibility in complex, holistic reasoning, they often exhibit high fidelity on focused, atomic sub-problems. Based on this, we propose Divergence-Guided Reasoning Curriculum (DGRC), which constructs a learning path from atomic knowledge to reasoning chains by dynamically deriving two complementary curricula from disagreements in reasoning pathways. When a student and teacher produce conflicting results, DGRC directs the teacher to perform a diagnostic analysis: it analyzes both reasoning paths to formulate atomic queries that target the specific points of divergence, and then self-answers these queries to create high-confidence atomic question-answer pairs. These pairs then serve a dual purpose: (1) providing an atomic curriculum to rectify the student's knowledge gaps, and (2) serving as factual criteria to filter the teacher's original reasoning chains, yielding a verified CoT curriculum that teaches the student how to integrate atomic knowledge into complete reasoning paths. Experiments across the medical and legal domains on student models of various sizes demonstrate the effectiveness of our DGRC framework. Notably, our method achieves a 7.76% relative improvement for the 1.5B student model in the medical domain over strong unlabeled baseline.

Mimic Human Cognition, Master Multi-Image Reasoning: A Meta-Action Framework for Enhanced Visual Understanding

While Multimodal Large Language Models (MLLMs) excel at single-image understanding, they exhibit significantly degraded performance in multi-image reasoning scenarios. Multi-image reasoning presents fundamental challenges including complex inter-relationships between images and scattered critical information across image sets. Inspired by human cognitive processes, we propose the Cognition-Inspired Meta-Action Framework (CINEMA), a novel approach that decomposes multi-image reasoning into five structured meta-actions: Global, Focus, Hint, Think, and Answer which explicitly modeling the sequential cognitive steps humans naturally employ. For cold-start training, we introduce a Retrieval-Based Tree Sampling strategy that generates high-quality meta-action trajectories to bootstrap the model with reasoning patterns. During reinforcement learning, we adopt a two-stage paradigm: an exploration phase with Diversity-Preserving Strategy to avoid entropy collapse, followed by an annealed exploitation phase with DAPO to gradually strengthen exploitation. To train our model, we construct a dataset of 57k cold-start and 58k reinforcement learning instances spanning multi-image, multi-frame, and single-image tasks. We conduct extensive evaluations on multi-image reasoning benchmarks, video understanding benchmarks, and single-image benchmarks, achieving competitive state-of-the-art performance on several key benchmarks. Our model surpasses GPT-4o on the MUIR and MVMath benchmarks and notably outperforms specialized video reasoning models on video understanding benchmarks, demonstrating the effectiveness and generalizability of our human cognition-inspired reasoning framework.

A 24-GHz CMOS Transformer-Based Three-Tline Series Doherty Power Amplifier Achieving 39% PAE

This paper presents a transformer-based three- transmission-line (Tline) series Doherty power amplifier (PA) implemented in 65-nm CMOS, targeting broadband K/Ka-band applications. By integrating an impedance-scaling network into the output matching structure, the design enables effective load modulation and reduced impedance transformation ratio (ITR) at power back-off when employing stacked cascode transistors. The PA demonstrates a -3-dB small-signal gain bandwidth from 22 to 32.5 GHz, a saturated output power (Psat) of 21.6 dBm, and a peak power-added efficiency (PAE) of 39%. At 6dB back-off, the PAE remains above 24%, validating its suitability for high- efficiency mm-wave phased-array transmitters in next-generation wireless systems.

An Area-Efficient 20-100-GHz Phase-Invariant Switch-Type Attenuator Achieving 0.1-dB Tuning Step in 65-nm CMOS

This paper presents a switch-type attenuator working from 20 to 100 GHz. The attenuator adopts a capacitive compensation technique to reduce phase error. The small resistors in this work are implemented with metal lines to reduce the intrinsic parasitic capacitance, which helps minimize the amplitude and phase errors over a wide frequency range. Moreover, the utilization of metal lines also reduces the chip area. In addition, a continuous tuning attenuation unit is employed to improve the overall attenuation accuracy of the attenuator. The passive attenuator is designed and fabricated in a standard 65nm CMOS. The measurement results reveal a relative attenuation range of 7.5 dB with a continuous tuning step within 20-100 GHz. The insertion loss is 1.6-3.8 dB within the operation band, while the return losses of all states are better than 11.5 dB. The RMS amplitude and phase errors are below 0.15 dB and 1.6{\deg}, respectively.

A Simple DropConnect Approach to Transfer-based Targeted Attack

We study the problem of transfer-based black-box attack, where adversarial samples generated using a single surrogate model are directly applied to target models. Compared with untargeted attacks, existing methods still have lower Attack Success Rates (ASRs) in the targeted setting, i.e., the obtained adversarial examples often overfit the surrogate model but fail to mislead other models. In this paper, we hypothesize that the pixels or features in these adversarial examples collaborate in a highly dependent manner to maximize the success of an adversarial attack on the surrogate model, which we refer to as perturbation co-adaptation. Then, we propose to Mitigate perturbation Co-adaptation by DropConnect (MCD) to enhance transferability, by creating diverse variants of surrogate model at each optimization iteration. We conduct extensive experiments across various CNN- and Transformer-based models to demonstrate the effectiveness of MCD. In the challenging scenario of transferring from a CNN-based model to Transformer-based models, MCD achieves 13% higher average ASRs compared with state-of-the-art baselines. MCD boosts the performance of self-ensemble methods by bringing in more diversification across the variants while reserving sufficient semantic information for each variant. In addition, MCD attains the highest performance gain when scaling the compute of crafting adversarial examples.

Online Supervised Subspace Tracking

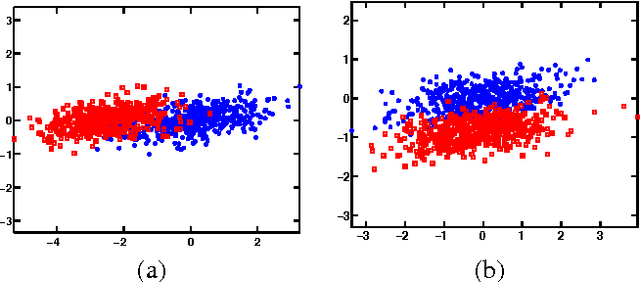
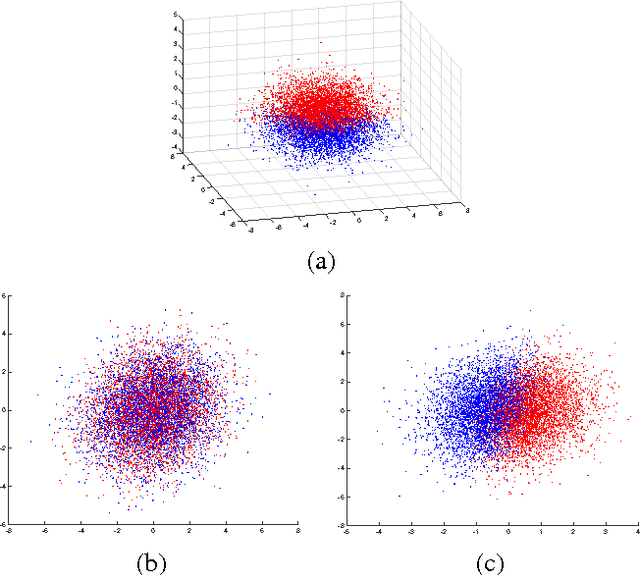
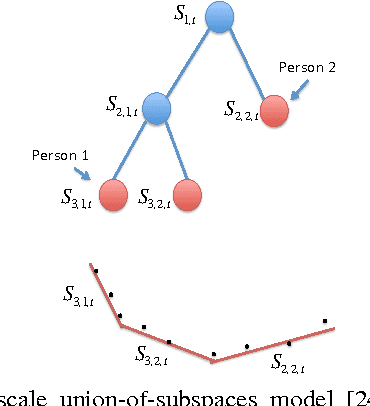
We present a framework for supervised subspace tracking, when there are two time series $x_t$ and $y_t$, one being the high-dimensional predictors and the other being the response variables and the subspace tracking needs to take into consideration of both sequences. It extends the classic online subspace tracking work which can be viewed as tracking of $x_t$ only. Our online sufficient dimensionality reduction (OSDR) is a meta-algorithm that can be applied to various cases including linear regression, logistic regression, multiple linear regression, multinomial logistic regression, support vector machine, the random dot product model and the multi-scale union-of-subspace model. OSDR reduces data-dimensionality on-the-fly with low-computational complexity and it can also handle missing data and dynamic data. OSDR uses an alternating minimization scheme and updates the subspace via gradient descent on the Grassmannian manifold. The subspace update can be performed efficiently utilizing the fact that the Grassmannian gradient with respect to the subspace in many settings is rank-one (or low-rank in certain cases). The optimization problem for OSDR is non-convex and hard to analyze in general; we provide convergence analysis of OSDR in a simple linear regression setting. The good performance of OSDR compared with the conventional unsupervised subspace tracking are demonstrated via numerical examples on simulated and real data.