InvertibleNetworks.jl: A Julia package for scalable normalizing flows

InvertibleNetworks.jl is a Julia package designed for the scalable implementation of normalizing flows, a method for density estimation and sampling in high-dimensional distributions. This package excels in memory efficiency by leveraging the inherent invertibility of normalizing flows, which significantly reduces memory requirements during backpropagation compared to existing normalizing flow packages that rely on automatic differentiation frameworks. InvertibleNetworks.jl has been adapted for diverse applications, including seismic imaging, medical imaging, and CO2 monitoring, demonstrating its effectiveness in learning high-dimensional distributions.

Learned multiphysics inversion with differentiable programming and machine learning

We present the Seismic Laboratory for Imaging and Modeling/Monitoring (SLIM) open-source software framework for computational geophysics and, more generally, inverse problems involving the wave-equation (e.g., seismic and medical ultrasound), regularization with learned priors, and learned neural surrogates for multiphase flow simulations. By integrating multiple layers of abstraction, our software is designed to be both readable and scalable. This allows researchers to easily formulate their problems in an abstract fashion while exploiting the latest developments in high-performance computing. We illustrate and demonstrate our design principles and their benefits by means of building a scalable prototype for permeability inversion from time-lapse crosswell seismic data, which aside from coupling of wave physics and multiphase flow, involves machine learning.

Amortized Normalizing Flows for Transcranial Ultrasound with Uncertainty Quantification

We present a novel approach to transcranial ultrasound computed tomography that utilizes normalizing flows to improve the speed of imaging and provide Bayesian uncertainty quantification. Our method combines physics-informed methods and data-driven methods to accelerate the reconstruction of the final image. We make use of a physics-informed summary statistic to incorporate the known ultrasound physics with the goal of compressing large incoming observations. This compression enables efficient training of the normalizing flow and standardizes the size of the data regardless of imaging configurations. The combinations of these methods results in fast uncertainty-aware image reconstruction that generalizes to a variety of transducer configurations. We evaluate our approach with in silico experiments and demonstrate that it can significantly improve the imaging speed while quantifying uncertainty. We validate the quality of our image reconstructions by comparing against the traditional physics-only method and also verify that our provided uncertainty is calibrated with the error.

Towards retrospective motion correction and reconstruction for clinical 3D brain MRI protocols with a reference contrast

Motion artifacts often spoil the radiological interpretation of MR images, and in the most severe cases the scan needs be repeated, with additional costs for the provider. We discuss the application of a novel 3D retrospective rigid motion correction and reconstruction scheme for MRI, which leverages multiple scans contained in a MR session. Typically, in a multi-contrast MR session, motion does not equally affect all the scans, and some motion-free scans are generally available, so that we can exploit their anatomic similarity. The uncorrupted scan is used as a reference in a generalized rigid-motion registration problem to remove the motion artifacts affecting the corrupted scans. We discuss the potential of the proposed algorithm with a prospective in-vivo study and clinical 3D brain protocols. This framework can be easily incorporated into the existing clinical practice with no disruption to the conventional workflow.

Reliable amortized variational inference with physics-based latent distribution correction

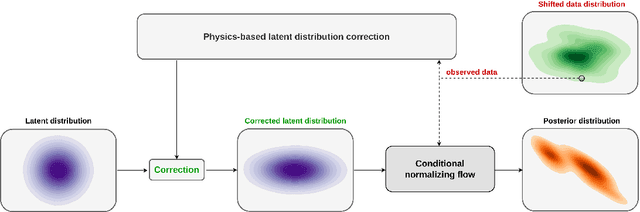
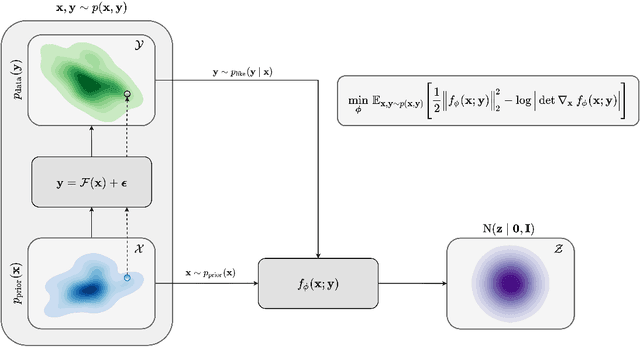
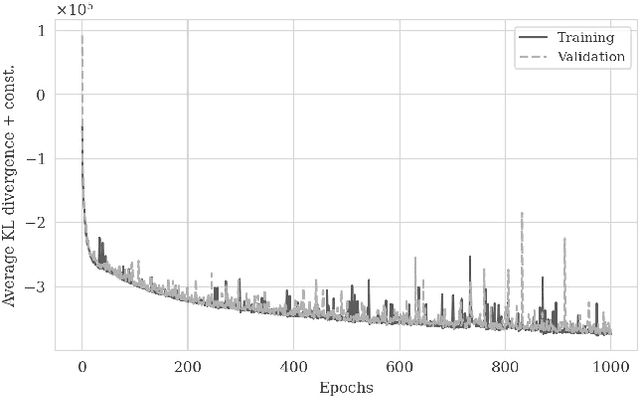
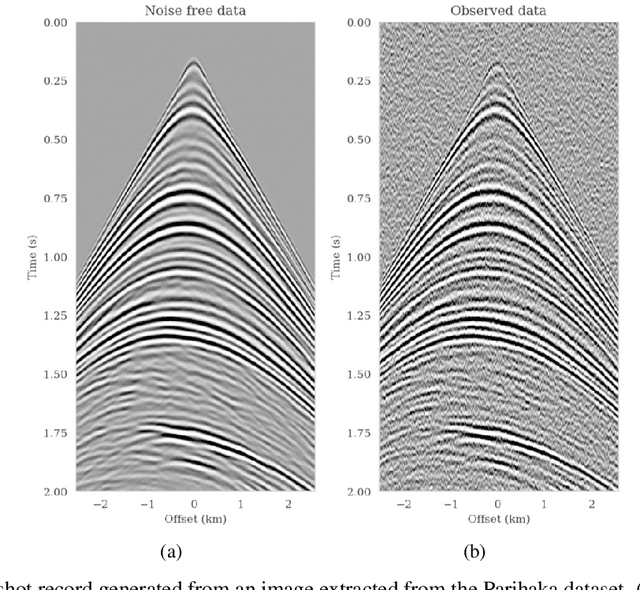
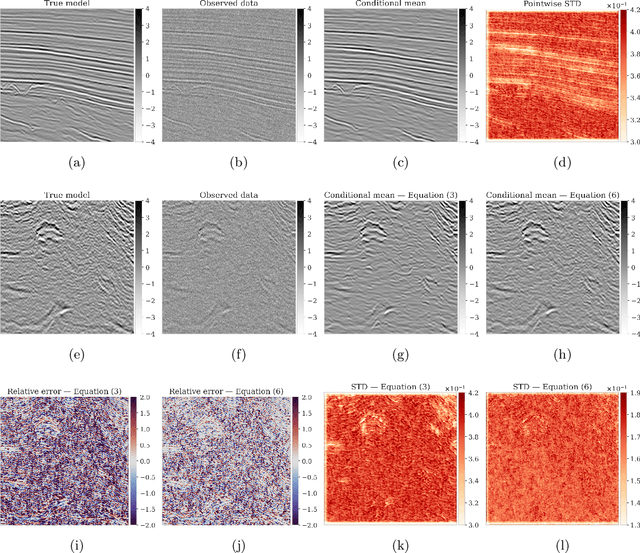
Bayesian inference for high-dimensional inverse problems is challenged by the computational costs of the forward operator and the selection of an appropriate prior distribution. Amortized variational inference addresses these challenges where a neural network is trained to approximate the posterior distribution over existing pairs of model and data. When fed previously unseen data and normally distributed latent samples as input, the pretrained deep neural network -- in our case a conditional normalizing flow -- provides posterior samples with virtually no cost. However, the accuracy of this approach relies on the availability of high-fidelity training data, which seldom exists in geophysical inverse problems due to the heterogeneous structure of the Earth. In addition, accurate amortized variational inference requires the observed data to be drawn from the training data distribution. As such, we propose to increase the resilience of amortized variational inference when faced with data distribution shift via a physics-based correction to the conditional normalizing flow latent distribution. To accomplish this, instead of a standard Gaussian latent distribution, we parameterize the latent distribution by a Gaussian distribution with an unknown mean and diagonal covariance. These unknown quantities are then estimated by minimizing the Kullback-Leibler divergence between the corrected and true posterior distributions. While generic and applicable to other inverse problems, by means of a seismic imaging example, we show that our correction step improves the robustness of amortized variational inference with respect to changes in number of source experiments, noise variance, and shifts in the prior distribution. This approach provides a seismic image with limited artifacts and an assessment of its uncertainty with approximately the same cost as five reverse-time migrations.

Deep Bayesian inference for seismic imaging with tasks

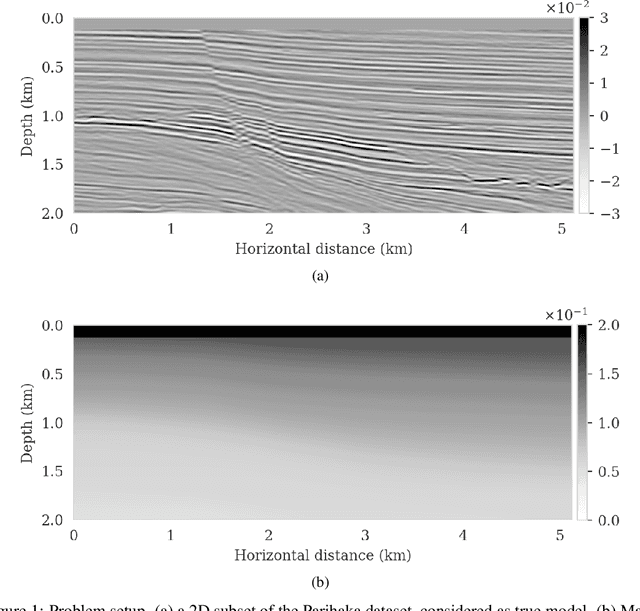
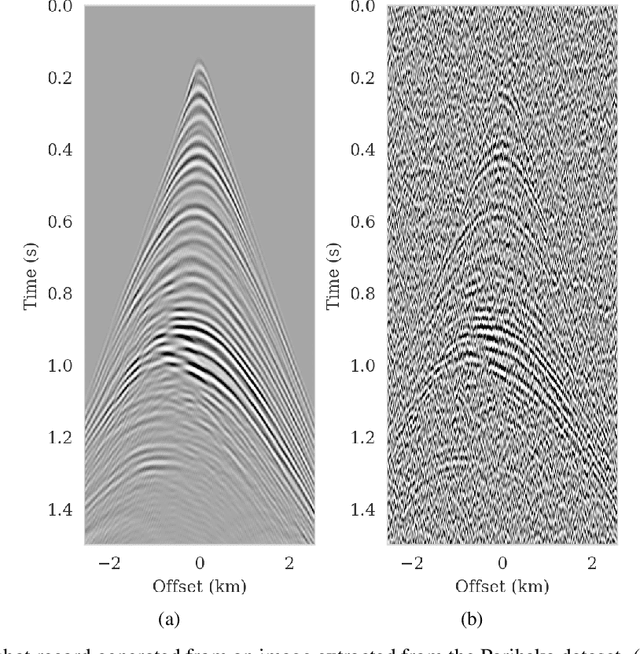
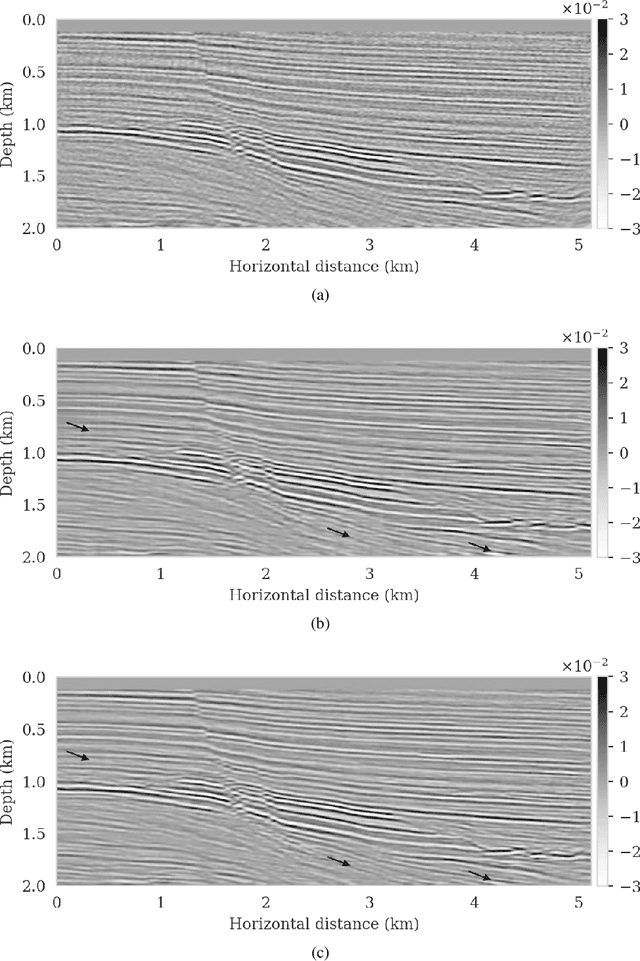
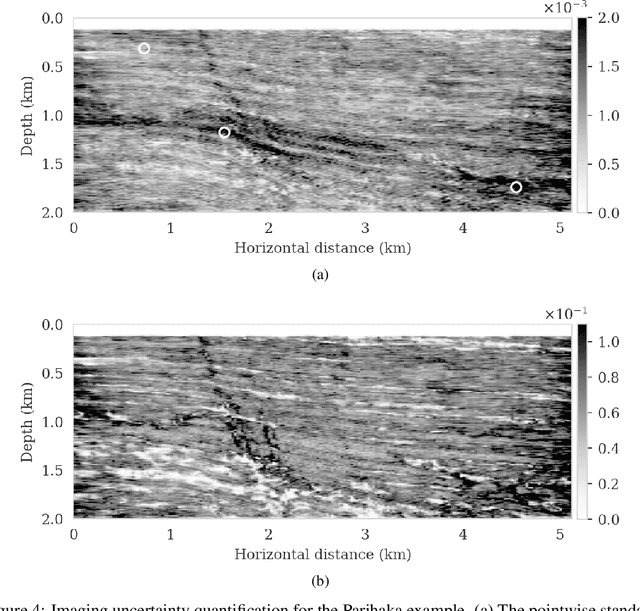
We propose to use techniques from Bayesian inference and deep neural networks to translate uncertainty in seismic imaging to uncertainty in tasks performed on the image, such as horizon tracking. Seismic imaging is an ill-posed inverse problem because of unavoidable bandwidth and aperture limitations, which that is hampered by the presence of noise and linearization errors. Many regularization methods, such as transform-domain sparsity promotion, have been designed to deal with the adverse effects of these errors, however, these methods run the risk of biasing the solution and do not provide information on uncertainty in the image space and how this uncertainty impacts certain tasks on the image. A systematic approach is proposed to translate uncertainty due to noise in the data to confidence intervals of automatically tracked horizons in the image. The uncertainty is characterized by a convolutional neural network (CNN) and to assess these uncertainties, samples are drawn from the posterior distribution of the CNN weights, used to parameterize the image. Compared to traditional priors, in the literature it is argued that these CNNs introduce a flexible inductive bias that is a surprisingly good fit for many diverse domains in imaging. The method of stochastic gradient Langevin dynamics is employed to sample from the posterior distribution. This method is designed to handle large scale Bayesian inference problems with computationally expensive forward operators as in seismic imaging. Aside from offering a robust alternative to maximum a posteriori estimate that is prone to overfitting, access to these samples allow us to translate uncertainty in the image, due to noise in the data, to uncertainty on the tracked horizons. For instance, it admits estimates for the pointwise standard deviation on the image and for confidence intervals on its automatically tracked horizons.

Preconditioned training of normalizing flows for variational inference in inverse problems

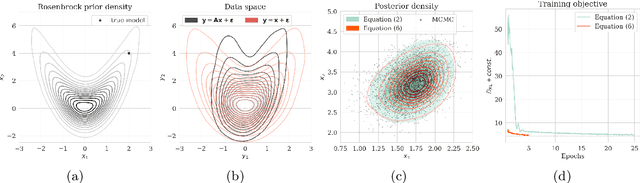
Obtaining samples from the posterior distribution of inverse problems with expensive forward operators is challenging especially when the unknowns involve the strongly heterogeneous Earth. To meet these challenges, we propose a preconditioning scheme involving a conditional normalizing flow (NF) capable of sampling from a low-fidelity posterior distribution directly. This conditional NF is used to speed up the training of the high-fidelity objective involving minimization of the Kullback-Leibler divergence between the predicted and the desired high-fidelity posterior density for indirect measurements at hand. To minimize costs associated with the forward operator, we initialize the high-fidelity NF with the weights of the pretrained low-fidelity NF, which is trained beforehand on available model and data pairs. Our numerical experiments, including a 2D toy and a seismic compressed sensing example, demonstrate that thanks to the preconditioning considerable speed-ups are achievable compared to training NFs from scratch.

Faster Uncertainty Quantification for Inverse Problems with Conditional Normalizing Flows

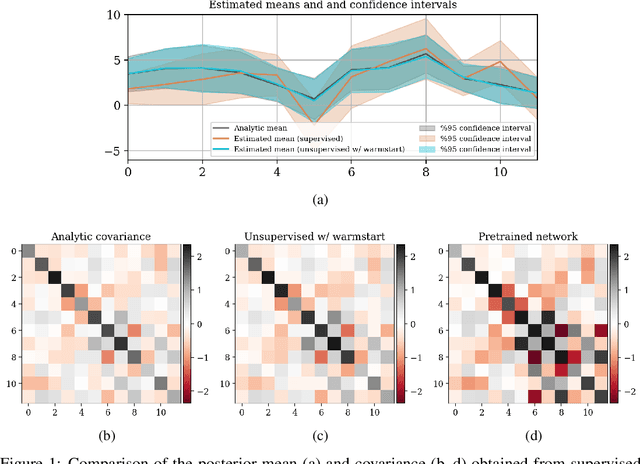
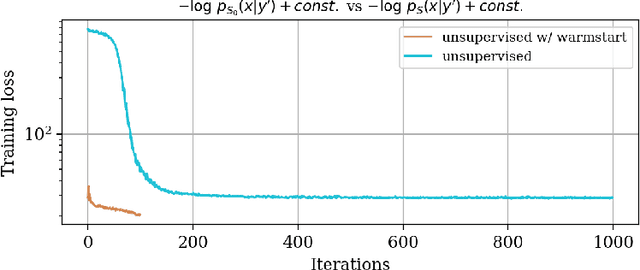
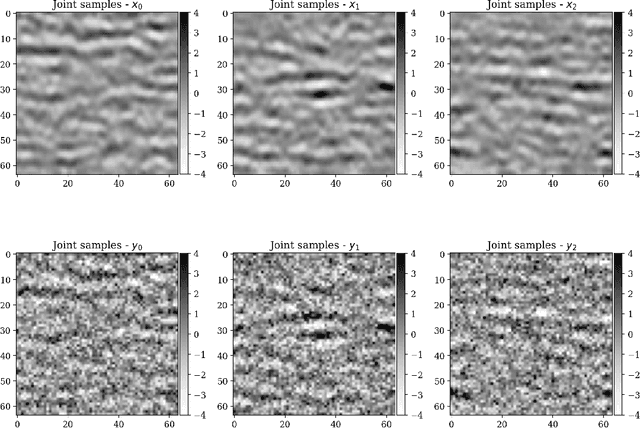
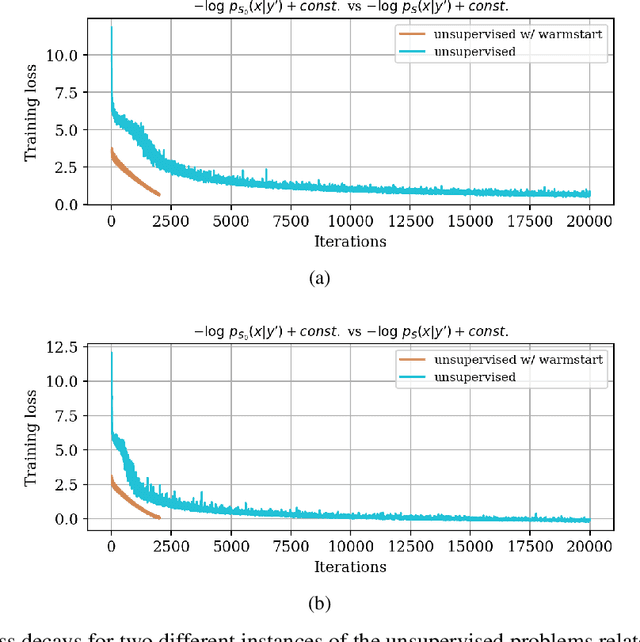
In inverse problems, we often have access to data consisting of paired samples $(x,y)\sim p_{X,Y}(x,y)$ where $y$ are partial observations of a physical system, and $x$ represents the unknowns of the problem. Under these circumstances, we can employ supervised training to learn a solution $x$ and its uncertainty from the observations $y$. We refer to this problem as the "supervised" case. However, the data $y\sim p_{Y}(y)$ collected at one point could be distributed differently than observations $y'\sim p_{Y}'(y')$, relevant for a current set of problems. In the context of Bayesian inference, we propose a two-step scheme, which makes use of normalizing flows and joint data to train a conditional generator $q_{\theta}(x|y)$ to approximate the target posterior density $p_{X|Y}(x|y)$. Additionally, this preliminary phase provides a density function $q_{\theta}(x|y)$, which can be recast as a prior for the "unsupervised" problem, e.g.~when only the observations $y'\sim p_{Y}'(y')$, a likelihood model $y'|x$, and a prior on $x'$ are known. We then train another invertible generator with output density $q'_{\phi}(x|y')$ specifically for $y'$, allowing us to sample from the posterior $p_{X|Y}'(x|y')$. We present some synthetic results that demonstrate considerable training speedup when reusing the pretrained network $q_{\theta}(x|y')$ as a warm start or preconditioning for approximating $p_{X|Y}'(x|y')$, instead of learning from scratch. This training modality can be interpreted as an instance of transfer learning. This result is particularly relevant for large-scale inverse problems that employ expensive numerical simulations.

Parameterizing uncertainty by deep invertible networks, an application to reservoir characterization

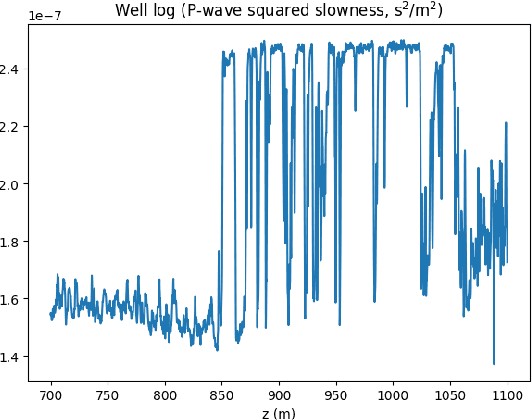
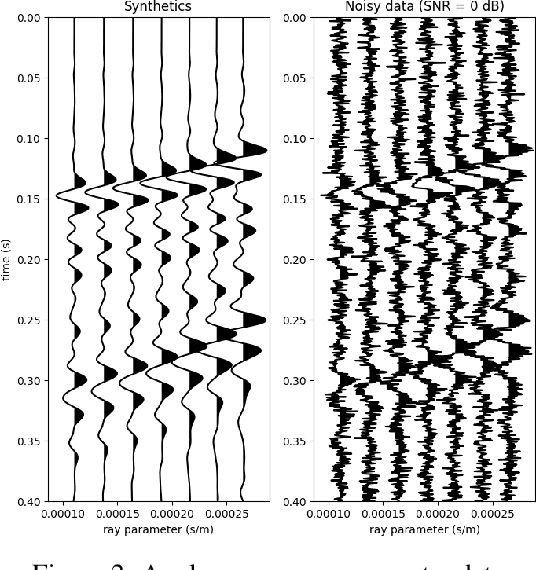
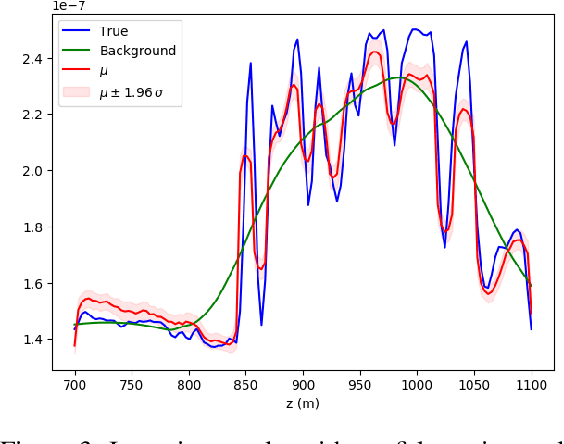
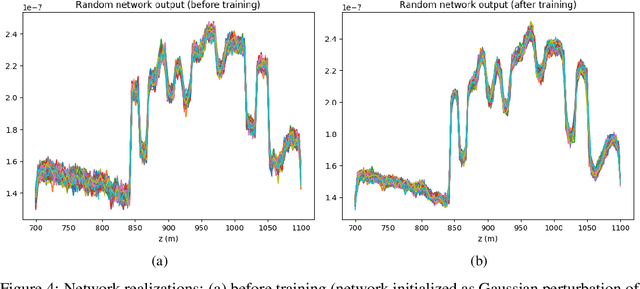
Uncertainty quantification for full-waveform inversion provides a probabilistic characterization of the ill-conditioning of the problem, comprising the sensitivity of the solution with respect to the starting model and data noise. This analysis allows to assess the confidence in the candidate solution and how it is reflected in the tasks that are typically performed after imaging (e.g., stratigraphic segmentation following reservoir characterization). Classically, uncertainty comes in the form of a probability distribution formulated from Bayesian principles, from which we seek to obtain samples. A popular solution involves Monte Carlo sampling. Here, we propose instead an approach characterized by training a deep network that "pushes forward" Gaussian random inputs into the model space (representing, for example, density or velocity) as if they were sampled from the actual posterior distribution. Such network is designed to solve a variational optimization problem based on the Kullback-Leibler divergence between the posterior and the network output distributions. This work is fundamentally rooted in recent developments for invertible networks. Special invertible architectures, besides being computational advantageous with respect to traditional networks, do also enable analytic computation of the output density function. Therefore, after training, these networks can be readily used as a new prior for a related inversion problem. This stands in stark contrast with Monte-Carlo methods, which only produce samples. We validate these ideas with an application to angle-versus-ray parameter analysis for reservoir characterization.

Uncertainty quantification in imaging and automatic horizon tracking: a Bayesian deep-prior based approach

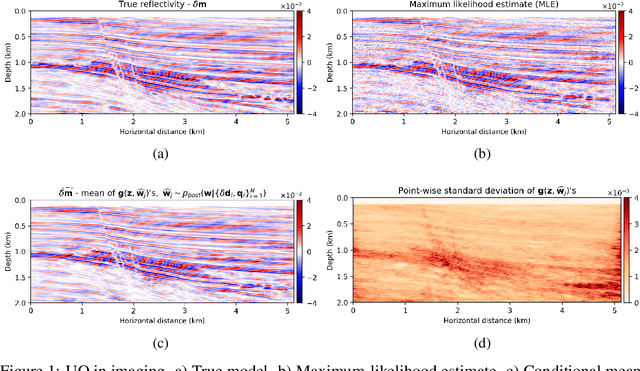
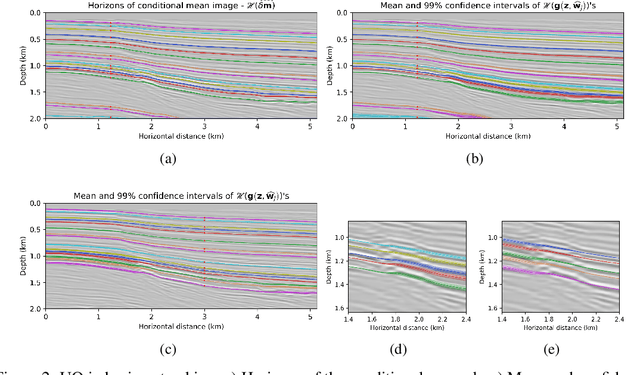
In inverse problems, uncertainty quantification (UQ) deals with a probabilistic description of the solution nonuniqueness and data noise sensitivity. Setting seismic imaging into a Bayesian framework allows for a principled way of studying uncertainty by solving for the model posterior distribution. Imaging, however, typically constitutes only the first stage of a sequential workflow, and UQ becomes even more relevant when applied to subsequent tasks that are highly sensitive to the inversion outcome. In this paper, we focus on how UQ trickles down to horizon tracking for the determination of stratigraphic models and investigate its sensitivity with respect to the imaging result. As such, the main contribution of this work consists in a data-guided approach to horizon tracking uncertainty analysis. This work is fundamentally based on a special reparameterization of reflectivity, known as "deep prior". Feasible models are restricted to the output of a convolutional neural network with a fixed input, while weights and biases are Gaussian random variables. Given a deep prior model, the network parameters are sampled from the posterior distribution via a Markov chain Monte Carlo method, from which the conditional mean and point-wise standard deviation of the inferred reflectivities are approximated. For each sample of the posterior distribution, a reflectivity is generated, and the horizons are tracked automatically. In this way, uncertainty on model parameters naturally translates to horizon tracking. As part of the validation for the proposed approach, we verified that the estimated confidence intervals for the horizon tracking coincide with geologically complex regions, such as faults.