Parameterizing uncertainty by deep invertible networks, an application to reservoir characterization
Paper and Code
Apr 16, 2020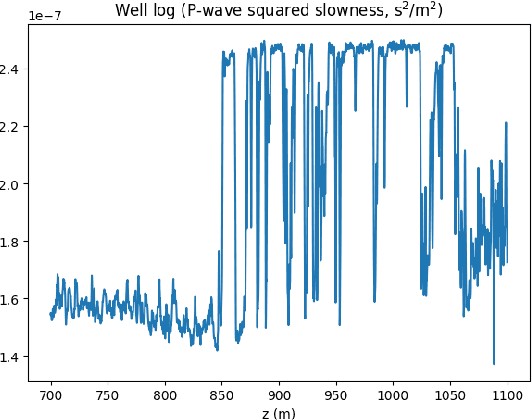
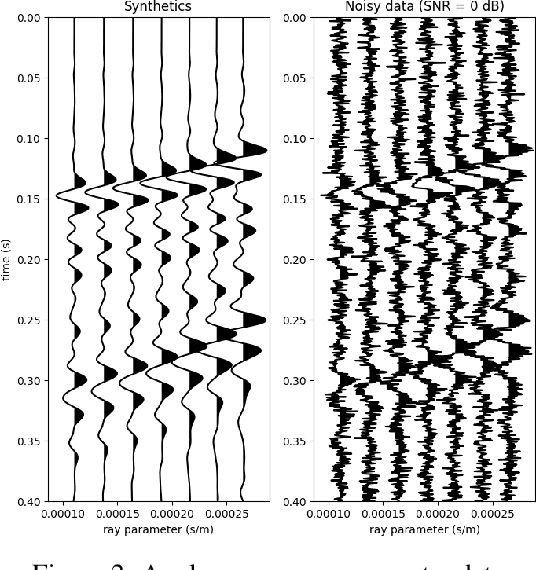
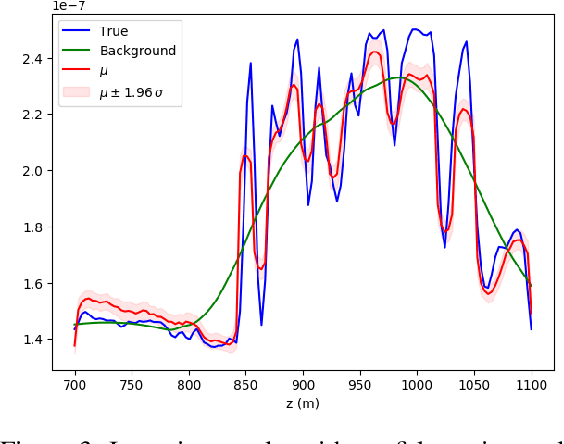
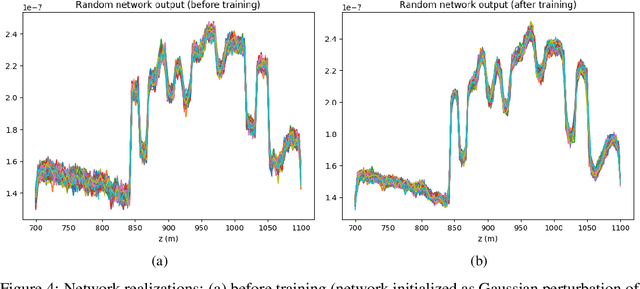
Uncertainty quantification for full-waveform inversion provides a probabilistic characterization of the ill-conditioning of the problem, comprising the sensitivity of the solution with respect to the starting model and data noise. This analysis allows to assess the confidence in the candidate solution and how it is reflected in the tasks that are typically performed after imaging (e.g., stratigraphic segmentation following reservoir characterization). Classically, uncertainty comes in the form of a probability distribution formulated from Bayesian principles, from which we seek to obtain samples. A popular solution involves Monte Carlo sampling. Here, we propose instead an approach characterized by training a deep network that "pushes forward" Gaussian random inputs into the model space (representing, for example, density or velocity) as if they were sampled from the actual posterior distribution. Such network is designed to solve a variational optimization problem based on the Kullback-Leibler divergence between the posterior and the network output distributions. This work is fundamentally rooted in recent developments for invertible networks. Special invertible architectures, besides being computational advantageous with respect to traditional networks, do also enable analytic computation of the output density function. Therefore, after training, these networks can be readily used as a new prior for a related inversion problem. This stands in stark contrast with Monte-Carlo methods, which only produce samples. We validate these ideas with an application to angle-versus-ray parameter analysis for reservoir characterization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge