Embed and Emulate: Contrastive representations for simulation-based inference

Scientific modeling and engineering applications rely heavily on parameter estimation methods to fit physical models and calibrate numerical simulations using real-world measurements. In the absence of analytic statistical models with tractable likelihoods, modern simulation-based inference (SBI) methods first use a numerical simulator to generate a dataset of parameters and simulated outputs. This dataset is then used to approximate the likelihood and estimate the system parameters given observation data. Several SBI methods employ machine learning emulators to accelerate data generation and parameter estimation. However, applying these approaches to high-dimensional physical systems remains challenging due to the cost and complexity of training high-dimensional emulators. This paper introduces Embed and Emulate (E&E): a new SBI method based on contrastive learning that efficiently handles high-dimensional data and complex, multimodal parameter posteriors. E&E learns a low-dimensional latent embedding of the data (i.e., a summary statistic) and a corresponding fast emulator in the latent space, eliminating the need to run expensive simulations or a high dimensional emulator during inference. We illustrate the theoretical properties of the learned latent space through a synthetic experiment and demonstrate superior performance over existing methods in a realistic, non-identifiable parameter estimation task using the high-dimensional, chaotic Lorenz 96 system.

Multimodal Learning for Crystalline Materials

Artificial intelligence (AI) has revolutionized the field of materials science by improving the prediction of properties and accelerating the discovery of novel materials. In recent years, publicly available material data repositories containing data for various material properties have grown rapidly. In this work, we introduce Multimodal Learning for Crystalline Materials (MLCM), a new method for training a foundation model for crystalline materials via multimodal alignment, where high-dimensional material properties (i.e. modalities) are connected in a shared latent space to produce highly useful material representations. We show the utility of MLCM on multiple axes: (i) MLCM achieves state-of-the-art performance for material property prediction on the challenging Materials Project database; (ii) MLCM enables a novel, highly accurate method for inverse design, allowing one to screen for stable material with desired properties; and (iii) MLCM allows the extraction of interpretable emergent features that may provide insight to material scientists. Further, we explore several novel methods for aligning an arbitrary number of modalities, improving upon prior art in multimodal learning that focuses on bimodal alignment. Our work brings innovations from the ongoing AI revolution into the domain of materials science and identifies materials as a testbed for the next generation of AI.

Training neural operators to preserve invariant measures of chaotic attractors

Chaotic systems make long-horizon forecasts difficult because small perturbations in initial conditions cause trajectories to diverge at an exponential rate. In this setting, neural operators trained to minimize squared error losses, while capable of accurate short-term forecasts, often fail to reproduce statistical or structural properties of the dynamics over longer time horizons and can yield degenerate results. In this paper, we propose an alternative framework designed to preserve invariant measures of chaotic attractors that characterize the time-invariant statistical properties of the dynamics. Specifically, in the multi-environment setting (where each sample trajectory is governed by slightly different dynamics), we consider two novel approaches to training with noisy data. First, we propose a loss based on the optimal transport distance between the observed dynamics and the neural operator outputs. This approach requires expert knowledge of the underlying physics to determine what statistical features should be included in the optimal transport loss. Second, we show that a contrastive learning framework, which does not require any specialized prior knowledge, can preserve statistical properties of the dynamics nearly as well as the optimal transport approach. On a variety of chaotic systems, our method is shown empirically to preserve invariant measures of chaotic attractors.

Deep Stochastic Mechanics

This paper introduces a novel deep-learning-based approach for numerical simulation of a time-evolving Schr\"odinger equation inspired by stochastic mechanics and generative diffusion models. Unlike existing approaches, which exhibit computational complexity that scales exponentially in the problem dimension, our method allows us to adapt to the latent low-dimensional structure of the wave function by sampling from the Markovian diffusion. Depending on the latent dimension, our method may have far lower computational complexity in higher dimensions. Moreover, we propose novel equations for stochastic quantum mechanics, resulting in linear computational complexity with respect to the number of dimensions. Numerical simulations verify our theoretical findings and show a significant advantage of our method compared to other deep-learning-based approaches used for quantum mechanics.

Model Stitching: Looking For Functional Similarity Between Representations

Model stitching (Lenc & Vedaldi 2015) is a compelling methodology to compare different neural network representations, because it allows us to measure to what degree they may be interchanged. We expand on a previous work from Bansal, Nakkiran & Barak which used model stitching to compare representations of the same shapes learned by differently seeded and/or trained neural networks of the same architecture. Our contribution enables us to compare the representations learned by layers with different shapes from neural networks with different architectures. We subsequently reveal unexpected behavior of model stitching. Namely, we find that stitching, based on convolutions, for small ResNets, can reach high accuracy if those layers come later in the first (sender) network than in the second (receiver), even if those layers are far apart.

Q-Flow: Generative Modeling for Differential Equations of Open Quantum Dynamics with Normalizing Flows

Studying the dynamics of open quantum systems holds the potential to enable breakthroughs both in fundamental physics and applications to quantum engineering and quantum computation. Due to the high-dimensional nature of the problem, customized deep generative neural networks have been instrumental in modeling the high-dimensional density matrix $\rho$, which is the key description for the dynamics of such systems. However, the complex-valued nature and normalization constraints of $\rho$, as well as its complicated dynamics, prohibit a seamless connection between open quantum systems and the recent advances in deep generative modeling. Here we lift that limitation by utilizing a reformulation of open quantum system dynamics to a partial differential equation (PDE) for a corresponding probability distribution $Q$, the Husimi Q function. Thus, we model the Q function seamlessly with off-the-shelf deep generative models such as normalizing flows. Additionally, we develop novel methods for learning normalizing flow evolution governed by high-dimensional PDEs, based on the Euler method and the application of the time-dependent variational principle. We name the resulting approach Q-Flow and demonstrate the scalability and efficiency of Q-Flow on open quantum system simulations, including the dissipative harmonic oscillator and the dissipative bosonic model. Q-Flow is superior to conventional PDE solvers and state-of-the-art physics-informed neural network solvers, especially in high-dimensional systems.

Discovering Conservation Laws using Optimal Transport and Manifold Learning

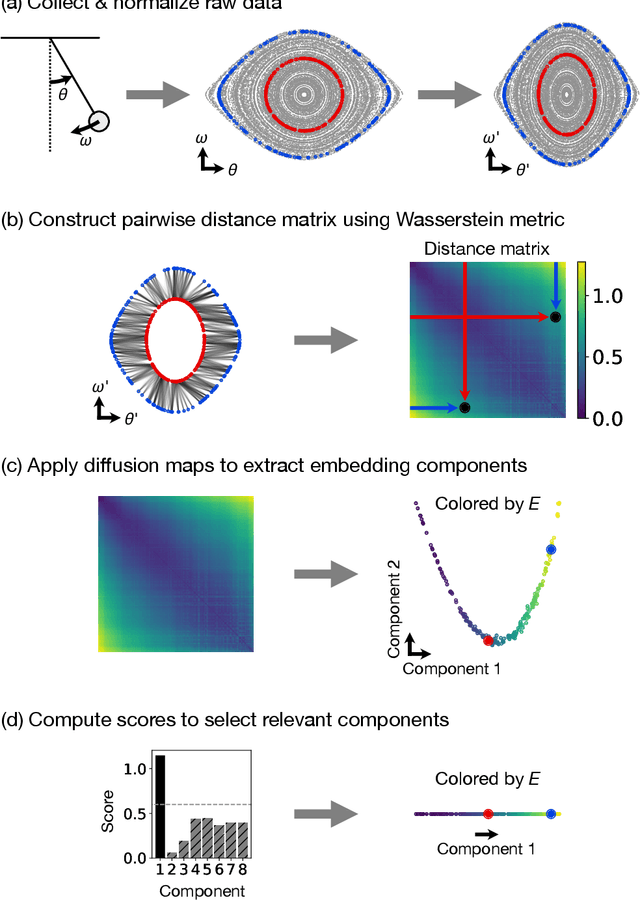
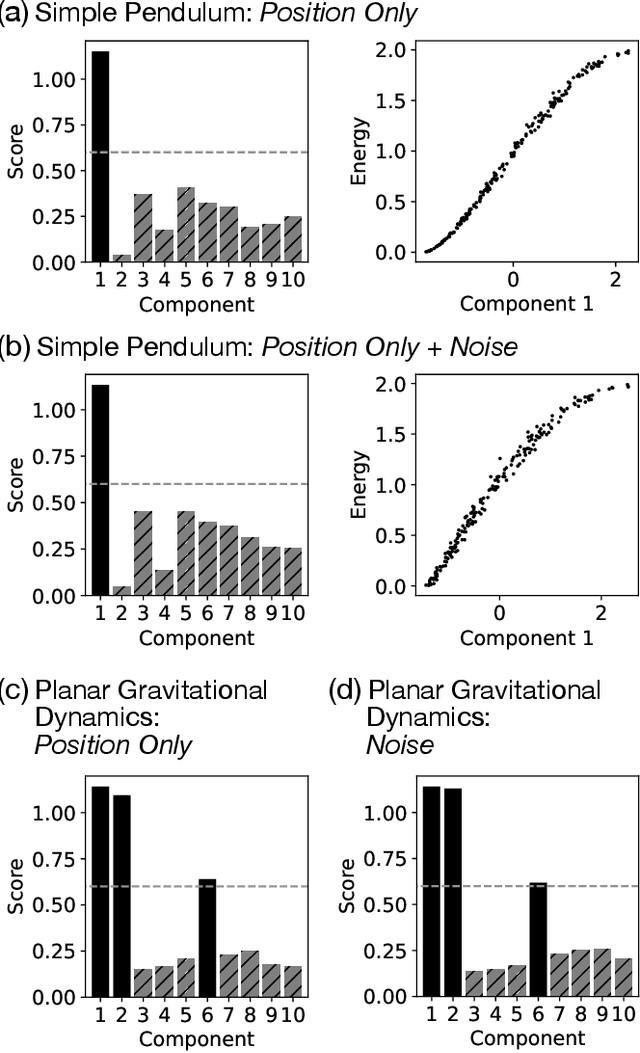
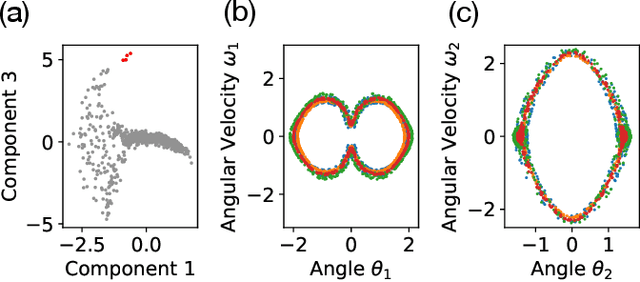
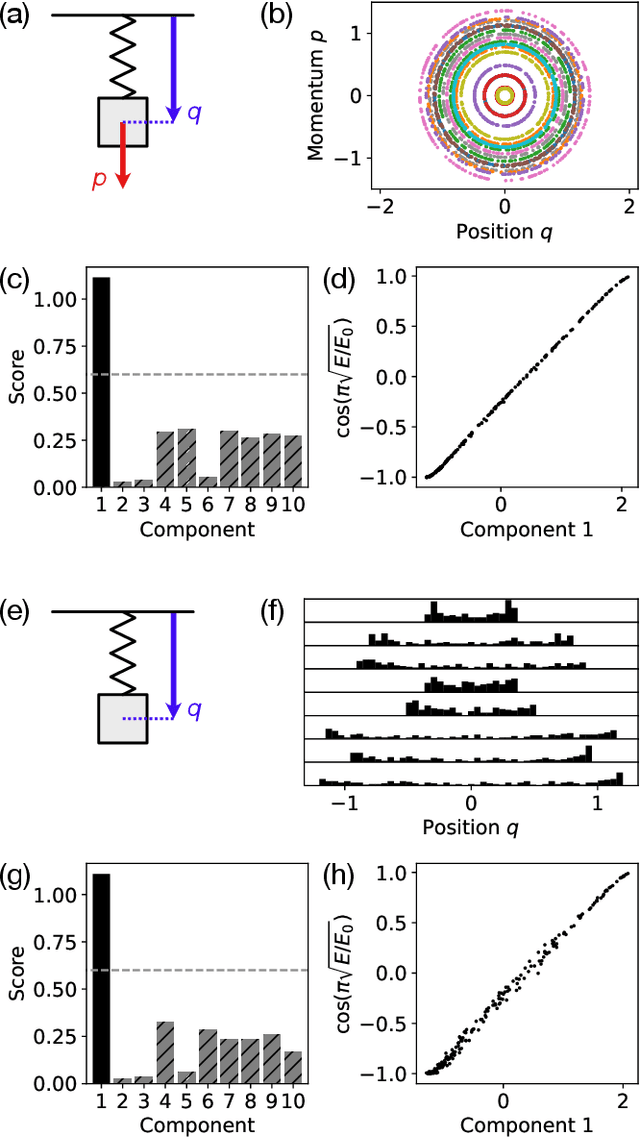
Conservation laws are key theoretical and practical tools for understanding, characterizing, and modeling nonlinear dynamical systems. However, for many complex dynamical systems, the corresponding conserved quantities are difficult to identify, making it hard to analyze their dynamics and build efficient, stable predictive models. Current approaches for discovering conservation laws often depend on detailed dynamical information, such as the equation of motion or fine-grained time measurements, with many recent proposals also relying on black box parametric deep learning methods. We instead reformulate this task as a manifold learning problem and propose a non-parametric approach, combining the Wasserstein metric from optimal transport with diffusion maps, to discover conserved quantities that vary across trajectories sampled from a dynamical system. We test this new approach on a variety of physical systems$\unicode{x2014}$including conservative Hamiltonian systems, dissipative systems, and spatiotemporal systems$\unicode{x2014}$and demonstrate that our manifold learning method is able to both identify the number of conserved quantities and extract their values. Using tools from optimal transport theory and manifold learning, our proposed method provides a direct geometric approach to identifying conservation laws that is both robust and interpretable without requiring an explicit model of the system nor accurate time information.

Deep Learning and Symbolic Regression for Discovering Parametric Equations

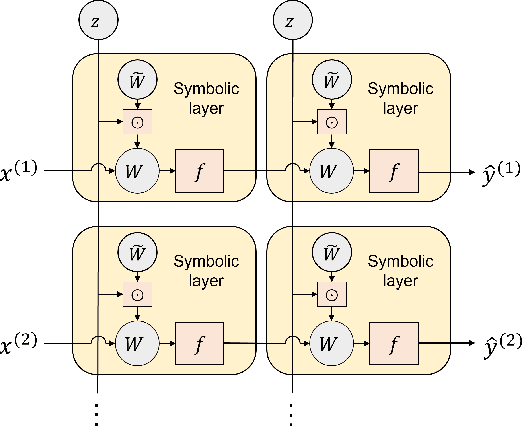
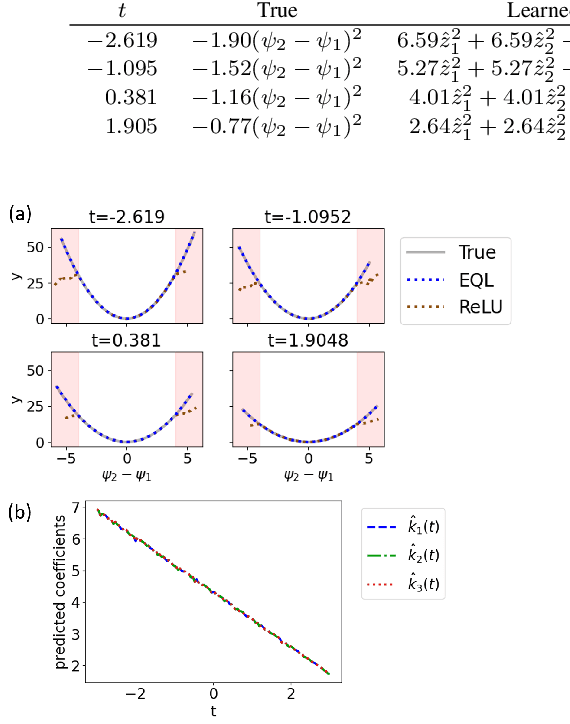
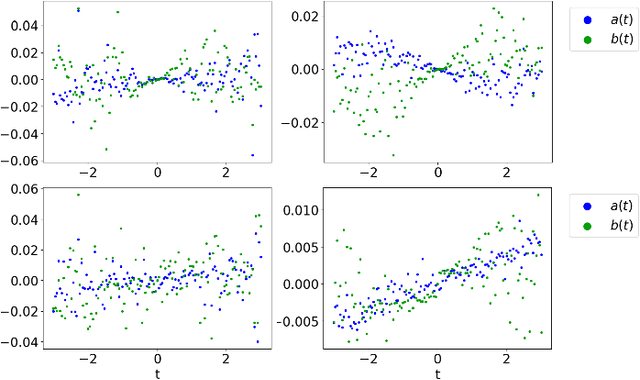
Symbolic regression is a machine learning technique that can learn the governing formulas of data and thus has the potential to transform scientific discovery. However, symbolic regression is still limited in the complexity and dimensionality of the systems that it can analyze. Deep learning on the other hand has transformed machine learning in its ability to analyze extremely complex and high-dimensional datasets. We propose a neural network architecture to extend symbolic regression to parametric systems where some coefficient may vary but the structure of the underlying governing equation remains constant. We demonstrate our method on various analytic expressions, ODEs, and PDEs with varying coefficients and show that it extrapolates well outside of the training domain. The neural network-based architecture can also integrate with other deep learning architectures so that it can analyze high-dimensional data while being trained end-to-end. To this end we integrate our architecture with convolutional neural networks to analyze 1D images of varying spring systems.

Discovering Sparse Interpretable Dynamics from Partial Observations

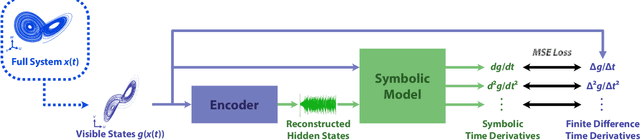
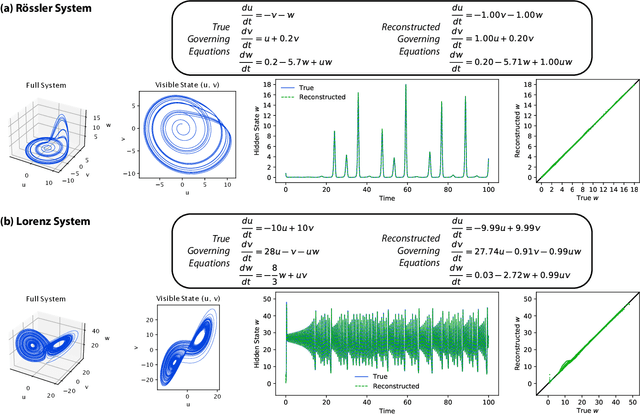
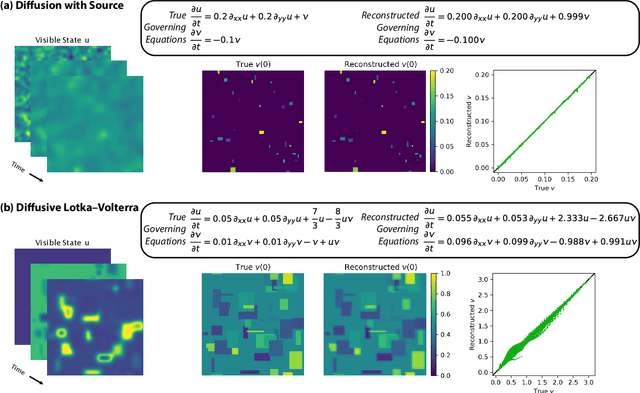
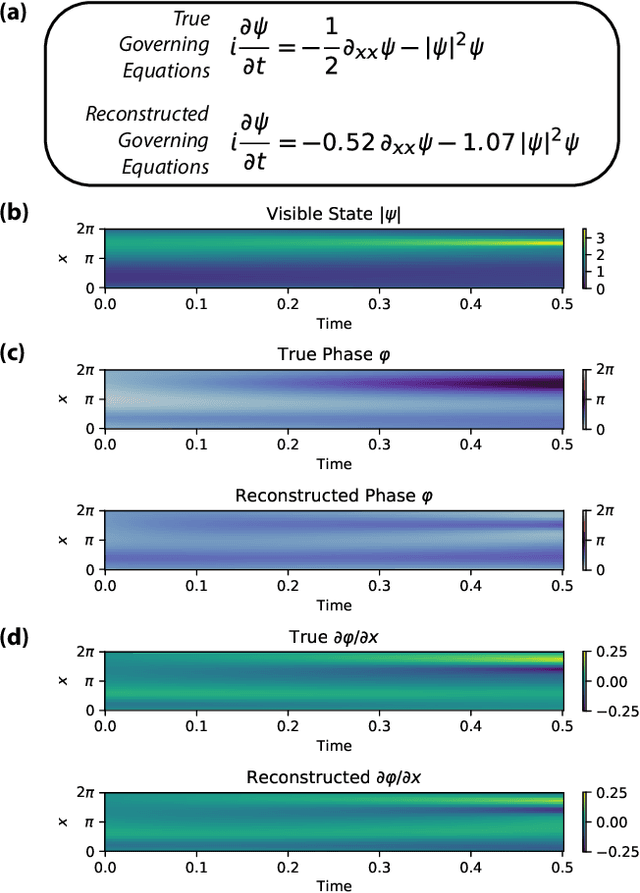
Identifying the governing equations of a nonlinear dynamical system is key to both understanding the physical features of the system and constructing an accurate model of the dynamics that generalizes well beyond the available data. We propose a machine learning framework for discovering these governing equations using only partial observations, combining an encoder for state reconstruction with a sparse symbolic model. Our tests show that this method can successfully reconstruct the full system state and identify the underlying dynamics for a variety of ODE and PDE systems.

Scalable and Flexible Deep Bayesian Optimization with Auxiliary Information for Scientific Problems

Bayesian optimization (BO) is a popular paradigm for global optimization of expensive black-box functions, but there are many domains where the function is not completely black-box. The data may have some known structure, e.g. symmetries, and the data generation process can yield useful intermediate or auxiliary information in addition to the value of the optimization objective. However, surrogate models traditionally employed in BO, such as Gaussian Processes (GPs), scale poorly with dataset size and struggle to incorporate known structure or auxiliary information. Instead, we propose performing BO on complex, structured problems by using Bayesian Neural Networks (BNNs), a class of scalable surrogate models that have the representation power and flexibility to handle structured data and exploit auxiliary information. We demonstrate BO on a number of realistic problems in physics and chemistry, including topology optimization of photonic crystal materials using convolutional neural networks, and chemical property optimization of molecules using graph neural networks. On these complex tasks, we show that BNNs often outperform GPs as surrogate models for BO in terms of both sampling efficiency and computational cost.